图的深度优先遍历：DFS遍历

图的深度优先遍历：DFS遍历

提示：系列图的文章
提示：大厂笔试面试都可能不咋考的数据结构：图

由于图的结构比较难，出题的时候，很难把这个图的数据搞通顺，而且搞通顺了题目也需要耗费太多时间，故笔试面试都不会咋考
笔试大厂考的就是你的贪心取巧策略和编码能力，这完全不必用图来考你，其他的有大量的选择
面试大厂考你的是优化算法的能力，但是图没啥可以优化的，只要数据结构统一，它的算法是固定死的，所以不会在面试中考！
万一考，那可能都是大厂和图相关的业务太多，比如美团高德地图啥的，这种考的少。

但不管考不考，我们要有基础，要了解图的数据结构和算法。万一考了呢，准备以备不时之需。

图的数据结构比较难，算法是固定的套路
咱们需要统一一种自己熟悉的图的数据结构，方便套用算法时好写！！

下面是咱们得关于图的重要基础知识和重点应用：
（1）图数据结构，图的统一数据结构和非标准图的转化算法
（2）图的宽度优先遍历：BFS遍历

---

图的深度优先遍历和二叉树的深度优先类似，只不过多了分叉

看看二叉树的先序遍历非递归实现DFS：
二叉树，二叉树的归先序遍历，中序遍历，后序遍历，递归和非递归实现

二叉树的dfs分为先序、中序和后序
咱们只说先序非递归实现方法：dfs

实际上就是用栈，逆序的功能来控制头左右打印输出

//复习（1）如果遇到x打印，然后先压右子，再压左子，弹出时，必定先弹出左子，再弹出右子
    //这不就是头、左、右吗？——先序遍历
    public static void unRecurrentPrePrint(Node head){
        if (head == null) return;

        Stack<Node> stack = new Stack<>();
        stack.push(head);//先压头
        while (!stack.isEmpty()){
            //首先打印头
            Node cur = stack.pop();
            System.out.print(cur.value + " ");
            //然后反着压，先压右边，再压左边，回头就是左右顺序出
            if (cur.right != null) stack.push(cur.right);
            if (cur.left != null) stack.push(cur.left);
        }
    }

图的深度优先遍历DFS：要理解透彻

咱们图的BFS和二叉树的BFS一样，
但是图的DFS跟二叉树的DFS并不完全一样，咱们要的不是逆序功能
咱要的是让栈记住沿途我走过的路径，方便回来之后找到旁支继续深度遍历
一条道走到黑 ！关键在两点：cur的邻居没遍历过的话， 再次压入cur ，只加一个邻居到栈里面， 立马break ；

具体咋实现呢？
一定要深刻理解一条道走到黑是如何用栈实现的
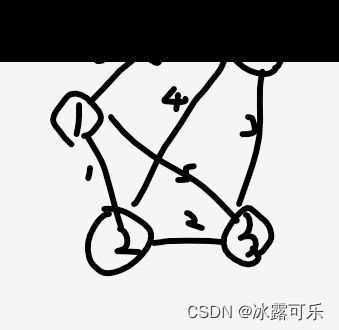
（1）head=1进栈，第一次压入时打印，后面压邻居才打印，set记录head（代表已经遍历过了）；
（2）cur=栈弹出的1，看cur的直接邻居，没进去过的，只要一个next=2，先将cur 再次压入 ，记住这条路，然后压入next=2，压入打印，set记录next，立马break；
（3）cur=栈弹出的2，看cur的直接邻居，没进去过的，只要一个next=3，先将cur 再次压入，记住这条路，然后压入next=3，压入打印，set记录next，立马break；
（4）cur=栈弹出的3，看cur的直接邻居，没进去过的，只要一个next=5，先将cur 再次压入，记住这条路，然后压入next=5，压入打印，set记录next，立马break；
（5）cur=栈弹出的5，看cur的直接邻居，自己邻居都进去过，不管；
（6）cur=栈弹出的3，看cur的直接邻居，自己邻居都进去过，不管；
（7）cur=栈弹出的2，看cur的直接邻居，自己邻居都进去过，不管；
（8）cur=栈弹出的1，看cur的直接邻居，没进去过的，只要一个next=4，先将cur 再次压入，记住这条路，然后压入next=4，压入打印，set记录next，立马break；
（9）cur=栈弹出的4，看cur的直接邻居，自己邻居都进去过，不管；
（10）cur=栈弹出的1，看cur的直接邻居，自己邻居都进去过，不管；
（11）栈空，结束

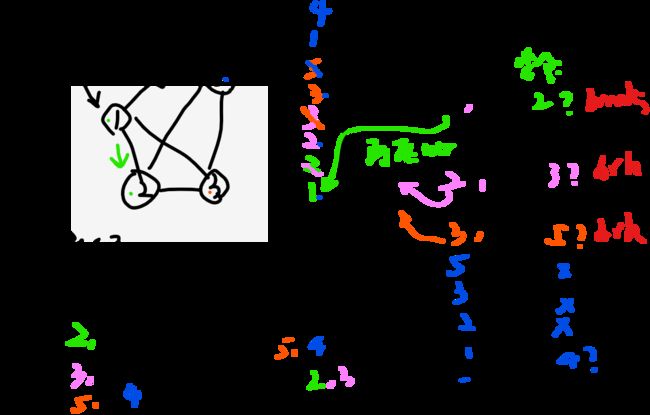
看见没，上面依次访问了 1 2 3 5 然后回去 5 3 2 1，然后才去的4
这就是一条道走到黑，通过栈，再次压入cur记住自己来过的路径，压入邻居打印邻居，然后立马break，保证直走一条道
这就是图的DFS原理，遍历过得点加入set，等整体栈为空，OK。

手撕代码，搞懂了这个流程，就非常非常简单了

//复习图的dfs
    public static void dfsReview(Node head){
        if (head == null) return;

        //一定要深刻理解一条道走到黑是如何用栈实现的
        Stack<Node> stack = new Stack<>();
        Set<Node> set = new HashSet<>();
        //（1）head=1进栈，第一次压入时打印，后面压邻居才打印，set记录head（代表已经遍历过了）；
        stack.push(head);
        System.out.print(head.value +" ");
        set.add(head);
        while (!stack.isEmpty()){
            //（2）cur=栈弹出的**1**，看cur的直接邻居，没进去过的，只要一个next=2，
            Node cur = stack.pop();
            for(Node next:cur.nexts){
                if (!set.contains(next)){
                    // 先将cur再次压入，记住这条路，然后压入next=2，压入打印，set记录next，立马break；
                    stack.push(cur);
                    stack.push(next);
                    System.out.print(next.value +" ");
                    set.add(next);
                    break;//立马退出循环
                }
            }
        }
    }

验证一下：
生成一个统一的丰富图结构：

//基础的数据类型，得自个写
    //边--和节点是相互渗透的俩数据结构
    public static class Edge{
        public int weight;
        public Node from;
        public Node to;
        public Edge(int w, Node a, Node b){
            weight = w;
            from = a;
            to = b;
        }
    }

    //节点
    public static class Node{
        public int in;
        public int out;
        public int value;
        public ArrayList<Node> nexts;
        public ArrayList<Edge> edges;//这里是相互渗透的，既然有邻居，就右边

        public Node(int v){
            value = v;//只需要给这么一个value即可
            in = 0;
            out = 0;
            nexts = new ArrayList<>();
            edges = new ArrayList<>();
        }
    }

    //图结构玩起来，图右边，节也有边
    public static class Graph{
        public HashMap<Integer, Node> nodes;//v,Node
        public HashSet<Edge> edges;
        public Graph(){
            nodes = new HashMap<>();//一般节点有value，对应包装袋，都是用哈希表玩的，并查集就是这么玩的
            edges = new HashSet<>();
        }

        public int getNodeNum(){
            return nodes.size();
        }

        public int getEdgeNum(){
            return edges.size();
        }
    }

    //将非标准图结构转化为左神标准图结构
    public static Graph generatGrap(int[][] matrix){
        if (matrix == null || matrix.length == 0) return null;
        //matrix==
        //[1,1,2]
        //[2,2,3]
        //[3,3,1],w,f,t
        //挨个遍历行
        Graph graph = new Graph();

        for (int i = 0; i < matrix.length; i++) {
            //建节点和边，然后装图，将节点的入度，出度，边和邻居放好
            int weight = matrix[i][0];
            int from = matrix[i][1];
            int to = matrix[i][2];

            //图中没节点，建，否则不必重复搞
            if (!graph.nodes.containsKey(from)) graph.nodes.put(from, new Node(from));
            if (!graph.nodes.containsKey(to)) graph.nodes.put(to, new Node(to));

            Node fromNode = graph.nodes.get(from);
            Node toNode = graph.nodes.get(to);//有就拿出来

            Edge edge = new Edge(weight, fromNode, toNode);//建边
            graph.edges.add(edge);

            fromNode.out++;
            toNode.in++;
            fromNode.nexts.add(toNode);
            fromNode.edges.add(edge);//除了入度说终点，其余都是说原点
        }

        return graph;
    }

public static void test(){
        int[][] matrix = {
                {1,1,2},
                {2,2,3},
                {3,3,5},
                {4,2,5},
                {5,1,3},
                {5,1,4}
        };
        Graph graph = generatGrap(matrix);
        System.out.println("bfs:");
        bfs(graph.nodes.get(1));//第一个节点开始遍历打印
        System.out.println("\n复习bfs:");
        bfsReview(graph.nodes.get(1));//第一个节点开始遍历打印


        System.out.println("\ndfs：");
        dfs(graph.nodes.get(1));//第一个节点开始遍历打印
        System.out.println("\n复习dfs：");
        dfsReview(graph.nodes.get(1));//第一个节点开始遍历打印

    }

bfs:
1 2 3 4 5 
复习bfs:
1 2 3 4 5 
dfs：
1 2 3 5 4 
复习dfs：
1 2 3 5 4 

前面那图的bfs也自己复习一下，非常非常简单的。

---

总结

提示：重要经验：

1）图的深度优先遍历dfs，思想的核心与二叉树的深度优先遍历有区别，主要是控制一条道走到黑，通过再次压入cur和压未被遍历过的邻居之后立马break来控制非常非常强大。
2）图的宽度优先遍历bfs用队列实现，图的深度优先遍历dfs用栈来实现，如果将来有人为你，如何用栈实现bfs，如何用队列实现dfs，它考你的不是真的bfs和dfs哦！而是考你如何用队列实现栈，如何用栈实现队列，再用你自己实现的队列去做bfs，用你自己实现的栈去实现dfs，可不就是【如何用栈实现bfs，如何用队列实现dfs】的本意吗？
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。