【学习笔记】机器学习基础--逻辑回归
系列文章目录
【第一章原理】【学习笔记】机器学习基础--线性回归_一无是处le的博客-CSDN博客
【第一章代码解释】 【线性回归】原生numpy实现波士顿房价预测_一无是处le的博客-CSDN博客
【第三章】传统机器学习【先不写】
【第四章】聚类算法【先不写】
【第五章原理】【学习笔记】深度学习基础----DNN_一无是处le的博客-CSDN博客
【第五章代码实现】【学习笔记】手写神经网络之word2vec_一无是处le的博客-CSDN博客
目录
系列文章目录
前言
一、【引入逻辑回归】
二、逻辑回归的介绍
定义与公式
三、激活函数
1.【引入激活函数】
2.sigmoid函数的定义和公式
四、损失函数
1.【引入损失函数】
2.KL距离
3.损失函数公式推导
五、梯度下降
--------------------------------------分割线---------------------------------------
六、补充/注意事项
1.为什么MSE不适用与逻辑回归？
2.多分类问题
3.如何解决线性不可分问题？
4.优化问题【重点】
5.分类阈值划分问题
6.样本不均衡问题
7.模型评估
8.同模型不同权重(系数)的影响
9.sigmoid函数推导（为什么要用sigmoid函数）
10.KL距离推导（为什么要用KL距离作为损失函数）
总结
前言
【学习笔记】机器学习基础--逻辑回归学习笔记，由浅入深理解逻辑回归，以下都是我自己个人的理解，如有错误欢迎指出啦！(●ˇ∀ˇ●)。本篇博客1.2w+字，写的很细，因为逻辑回归可以说是机器学习最本质的东西，后面的深度学习都是基于逻辑回归的，因此我将本篇化为重点，用大量笔墨描述。
一、【引入逻辑回归】
从我的上一篇博客中，我们已经知道了机器学习的一些基本流程，本篇博客会继续完善一些优化类的方法和一个新的机器学习方向----分类。而分类问题，我们入门需要学习的就是逻辑回归。而逻辑回归，我们可以看作是线性回归的延续，只是应用的方向不同（线性回归知道一个点来预测另一个点【拟合】，而逻辑回归是知道完整的坐标来计算点的相对位置【分类】），其中的很多思想都与线性回归是一样的，如果有些不懂的线性回归知识或者我没有提到的，可以去参考一下我的上篇博客----线性回归原理。
分类问题也分为二分类和多分类，为了更直观的表现和证明，我们这里通篇采用二分类（
之所以不写多分类，一个是因为需要写的东西太多，太复杂，二是因为二分类问题可以拓展成为多分类，而且工程中也大多是这样做的）。
二、逻辑回归的介绍
定义与公式
逻辑回归是一种常用的分类算法，它用于将输入特征与二元输出变量之间的关系建模。在逻辑回归中，输出变量是二元的，即只能取0或1两个值，因此逻辑回归可以被看作是一种二元分类算法。
逻辑回归的基本公式如下：
其中，p(y=1|x)表示在给定输入x的情况下输出y=1的概率，e是自然对数的底数，d是线性函数的值：
d = w^T x + b
其中，w和b分别是模型的权重向量和偏置项（bias），x是输入特征向量，w^T表示向量w的转置。
对于二元输出变量，我们通常将其表示为y=1或y=0。因此，当d大于0时，p(y=1|x)的值就更接近于1，当d小于0时，p(y=1|x)的值就更接近于0。在模型学习的过程中，我们可以使用最大似然估计等方法来优化模型的参数，以最大化正确分类（或最小化损失函数）。
上面是GPT给的标准答案，从上面我们可以看出，其公式就是我们上一篇博客讲的线性回归的公式，只不过这里多加了一个激活函数sigmoid函数，用来给每个结果加权，最终概率最大的那个结果作为最终输出，如下图：
这就可以看作是逻辑回归的基本原理了。但是现在我们并不知道什么是sigmoid函数和为什么要用这个函数，下面我会一一将这些道来。
三、激活函数
1.【引入激活函数】
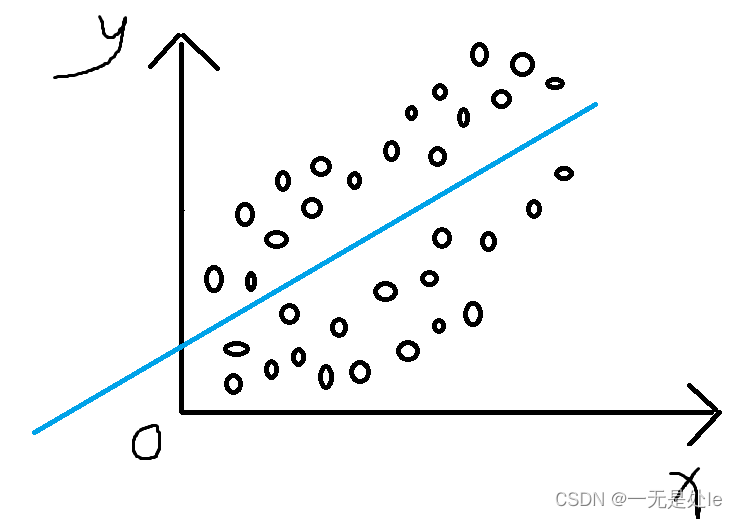
我们如果需要实现一个二分类问题，可以如何实现，我能想到的最简单的二分类如下：
就是使用最简单的线性回归找出一条直线 
，我这里给定义y>0为一类，y<=0为一类，这就是最简单的二分类。
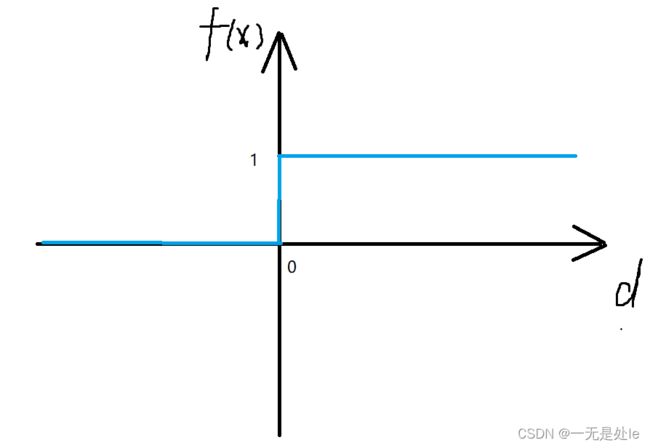
现在我们要对这个函数的结果进行激活，也就是要输出结果，那么这个二分类最终的结果输出函数可以表示为
，分类曲线如下：
如图所示，这就是我们一下子就能想到的最简单的二分类曲线，但是这样的曲线存在什么问题呢？曲线太硬了，输出结果非0即1，只能带来分类信息而不能带来程度量信息，而少量的信息会达不到我们最终理想的效果。举个例子，假设我们现在要做一个图片分类，区分图片中的斑马和一般的马，假如一般的马的身上因为某些原因出现了一些斑点，那么哪怕d的结果是0.01，也会被认为是斑马，因此这样的分类曲线会在实际工程中造成很大的误差，也难以应用。因此，我们需要寻找一个相对平滑过渡的曲线，能代表不同权重的平滑曲线，这样我们之后调整特征权重也会变得简单，信息量增大，在实际中应用分类的结果也会越好，因此，就有数学家提出了一个比较好的分类曲线----sigmoid函数。
2.sigmoid函数的定义和公式
sigmoid函数（又称为Logistic函数）是逻辑回归模型中常用的激活函数，它将任何实数压缩到[0,1]的区间上，并且其输出值可以被解释为对应于输入的概率值。
sigmoid函数的基本公式如下：
其中，x是一个实数，e是自然对数的底数。当x越大，f(x)越接近于1；当x越小，f(x)越接近于0。sigmoid函数具有平滑并且连续的性质，在训练神经网络等模型时，sigmoid函数能够帮助梯度下降算法更快速地收敛。
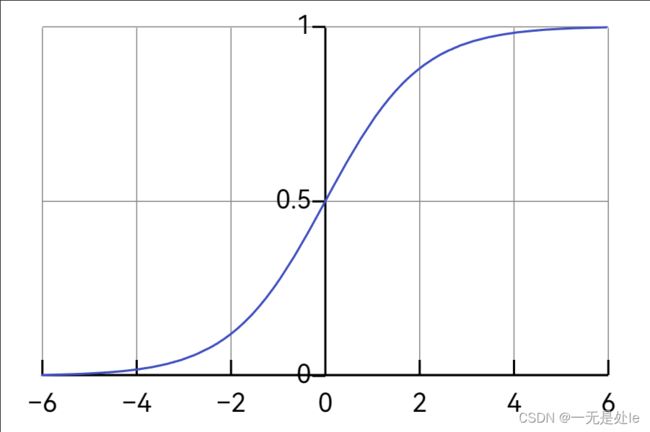
sigmoid函数的图像如下：
这样的曲线就符合了我们的要求。
四、损失函数
1.【引入损失函数】
由分类曲线的定义我们可以知道，在离分类线越远的点，其分类正确的概率也就越大（越接近1或0），离分类线越近的点，其分类正确的概率越小（接近0.5），也就是说，我们的目标是需要不断调整w来使得最终的概率更接近目标值【即
越小越好】，因此我们可以使用这一点来作为损失函数。（
其实这个跟线性回归中的MSE也有很大的相似点，本质思想其实类似）那我们能否使用线性回归的损失函数（作为欧氏距离，看似可行）呢？答案是不能的，至于为什么，我后面会写道。因此我们需要使用一种新的距离来度量预测值和真实值----KL距离（想了解的可以自己去学习，这里只用来推导损失函数）。
2.KL距离
【看看就好】
KL（Kullback-Leibler）距离，也称为相对熵，是衡量两个概率分布之间差异的一种度量方式。假设有两个离散概率分布 P、Q，它们分别由概率质量函数 p(x) 和 q(x) 给出，KL距离表示为 D_KL(P||Q)，定义为 P 和 Q 的交叉熵 H(P,Q) 减去 P 的熵 H(P)：
D_KL(P||Q) = H(P, Q) - H(P)
其中，熵 H(P) 用来衡量随机变量的不确定性，公式为：
H(P) = -∑_x p(x) * log p(x)
交叉熵 H(P,Q) 表示当我们使用错误的模型 Q 来近似真实的概率分布 P 时所需要额外增加的平均编码长度，公式为：
H(P,Q) = -∑_x p(x) * log q(x)
由于 KL 距离是一种度量方式，所以它满足以下性质：
- 非负性：D_KL(P||Q) >= 0，且仅在 P = Q 时等于0；
- 非对称性：D_KL(P||Q) ≠ D_KL(Q||P)；
- 稳定性：KL 距离具有模型不变性，即 KL 距离在模型缩放、平移或变换后仍保持不 变。
这是GPT给出的标准答案，看着很乱不好理解，换一种方式表达他的公式为：
他们的差异体现在log上，如果两个概率相同的话，kl距离为0（log1=0），即预测值和真实值完全相同，完美分类。
但是要注意：KL距离虽然可以看似距离，但是它又不具备距离的一些性质，例如对称性。我们知道欧氏距离是具有对称性的，A到B的距离和B到A的距离是一样的，但是KL距离就不能这样看待，因为如果将p和q互换的话，他们的计算结果就不同（除非两个完全一样）。
变种：当分布为连续的点（也就是曲线的情况下），我们则需要将累加符号替换成积分号。
提出问题1：p(x)为真实值，q(x)为预测值，当 时，下图中q1和q2哪个最终的KL值小？
我们先将公式化简为：
，我们从公式中可以看出，
这第一部分的值是固定的（px是真实值）也就是说我们只需要看 
这一部分，我们想要KL值小就需要这一部分尽可能的大，同时需要满足px和qx尽可能的接近， 那么毫无疑问，我们需要遵循抓大放小原则，需要尽可能保证大的px权重值的情况下qx大，因此这个情况下，我们认为q1的效果会更好。
提出问题2：同样的情况下如果将px和qx交换位置，结果如何？
同样的我们先将公式化简：
，同样的 
这一部分的值是固定的（q曲线的位置不同只会影响分类效果，但是其大小不会改变），也就是我们同样只需要看 
这一部分，这种情况就不能用抓大放小了，因为q的位置是不确定的，我们只能看p，这种情况下由于log的影响，px越小的情况下其值越接近负无穷，因此我们想要这部分大的话就需要抵消负无穷带来的影响，因此我们需要qx尽可能的小并且同时需要满足px和qx尽可能的接近，因此这个问题的回答是q1的效果更好。
这两个问题也回答了KL距离不具有对称性的性质。
3.损失函数公式推导
我们上面提到KL距离能很好的作为分类情况下的度量函数，那么是否意味着我们可以直接使用
这个公式看似复杂，实际上只是两个相同的部分罢了，第一部分负责px=1，第二部分负责px=0。那么我们将这个公式展开我们就会发现，这两部分当中都有一小部分存在log1，也就是说这部分没用，我们再将他化简平均，并换用更为直观的表达得到：
(这里f表示预测值，y表示真实值)
而这个函数，就可以作为逻辑回归的损失函数，而这个损失函数，也被称为交叉熵损失或者对数似然损失，这是分类学习中通常使用的损失函数。
![f(x)=\sum_{i=1}^{n}\left \{ p(x_{i})*log\frac{p(x_{i})}{q(x_{i})}+\left [ 1-p(x_{i}) \right ]*log\frac{(1-p(x_{i}))}{1-(q(x_{i}))} \right \}](http://img.e-com-net.com/image/info8/ea6c75ecfe6342daa4bcedcc2d1fce27.png){kind=small}
补充：写到这里的时候我就想到，给KL距离增加一块让他能处理px=0的情况，但是同样的，这里没有考虑qx=0的情况，如果出现了哪怕一个，计算机都无法计算这种无穷之，会直接溢出报异常，但是细想之后实际情况下是不会出现这种情况的，因为我们用的激活函数是sigmoid函数，不存在为0或者为1的情况，这也可以作为我们为什么不使用开头那种”硬“的激活函数的理由。
五、梯度下降
这里就不赘述梯度下降的原理，如有需要可以看我上一篇博客--(1条消息) 【学习笔记】机器学习基础--线性回归_一无是处le的博客-CSDN博客这里我们就直接对损失函数进行微分，我们先将所有需要求解的函数罗列出来：
那么我们直接对cost进行微分:
【微分的链式法则】
则
（
注意在python中log默认为ln，因此这里求导才会直接得到 1/fi 而非1/fi*lnfi）化简得：
则梯度
带入计算即可。
![\frac{\partial cost}{\partial w}=\frac{-1}{n}\sum_{i=1}^{n}\left [ y_{i}(1-f_{i})-(1-y_{i})f_{i} \right ]x](http://img.e-com-net.com/image/info8/766f9413112c43e5b726d692a61b0326.png){kind=small}
--------------------------------------分割线---------------------------------------
至此，我们基本已经对逻辑回归有了一定程度的理解，因此，下面继续分享一些逻辑回归的性质
六、补充/注意事项
1.为什么MSE不适用与逻辑回归？
按道理，这个是能看作欧氏距离，也可以作为预测值与真实值之间的损失，那么为什么逻辑回归的分类问题中不用MSE作为损失函数呢？
我们先试着把MSE带入到逻辑回归中，求导得：
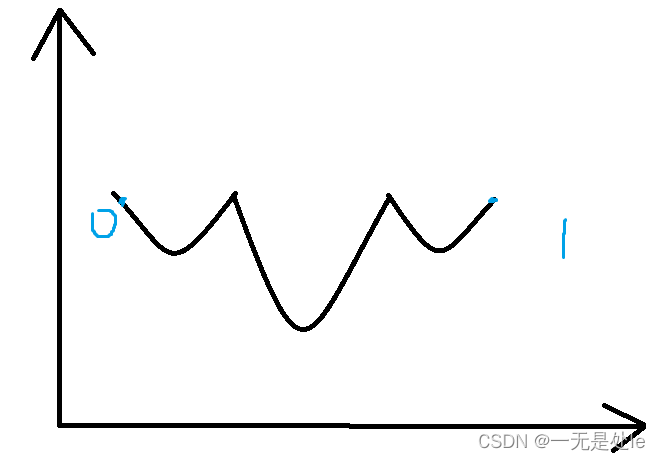
那么问题就很明显了，这个导数有一个很严重的问题，因为其中的w开始是一个随机数，如果这个数很大或者很小，那么无论你x取什么值 fi 都是趋近于1或0，那么整个导数就会趋近于0，w也几乎不会发生太大的变化，仅凭这一个问题就直接否定了MSE作为逻辑回归的损失函数。用理论证明的话就是这个损失函数的曲线如下：
这个损失函数曲线不是一个凸函数，因此如果当w取到很大或者很小的时候，梯度下降是无法寻找到最优解。
这时候有人可能会问：如果多找几个初始值，或者用特殊的方法让初始值在一些特定的区域，不就行了。其实，这些方法可能有些用处，但是在真正的工程上，大多时候都是用不到的，因为现在作图之所以只有两个极小值点点是因为维度低，但是在工程上我们一般遇到的都是高维的数据，可能成百上千维，这个时候的极小值点可能有成千上万个（局部极小值点 和 维数的平方 成正比），这个时候再去做初始值问题就失去了意义。
2.多分类问题
我们这里都是基于二分类写的，那么我们如果要进行多分类的话需要怎么做呢？有两种方法，一个是直接构建n个二分类模型【OVR--一对多】（一类为分类中的正类，其他所有类为负类，
类似于决策树的结构，我个人理解，结果取概率最大的那一正类，如果概率都很小则不属于任何一类），另一种方法是对多分类直接全部放入，两两组合【OVO--一对一】，这需要C(n, 2) 个分类器，分别计算每一个类别的概率，取正类，结果取出现次数最多的那一个正类。这两种方法是目前使用最多的使用逻辑回归解决多分类问题的方法，他们也有优劣，第一种方法使用最广泛，模型简单，效率相对较好，但是容易造成训练集样本数量的不平衡（Unbalance），尤其在类别较多的情况下，经常容易出现正类样本的数量远远不及负类样本的数量，这样就会造成分类器的偏向性。第二种方法优点也很明显，它在一定程度上规避了数据集 unbalance 的情况，性能相对稳定，并且需要训练的模型数虽然增多，但是每次训练时训练集的数量都降低很多，其训练效率会提高。
详细了解参考：[机器学习-原理与实践]逻辑回归(LogisticRegression)多分类(OvR, OvO, MvM）_ovo逻辑回归_茫茫人海一粒沙的博客-CSDN博客
https://blog.csdn.net/keeppractice/article/details/107088538?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522168921283516800188586540%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=168921283516800188586540&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-1-107088538-null-null.142%5Ev88%5Econtrol_2,239%5Ev2%5Einsert_chatgpt&utm_term=%E9%80%BB%E8%BE%91%E5%9B%9E%E5%BD%92ovr%E5%AE%9E%E7%8E%B0&spm=1018.2226.3001.4187
3.如何解决线性不可分问题？
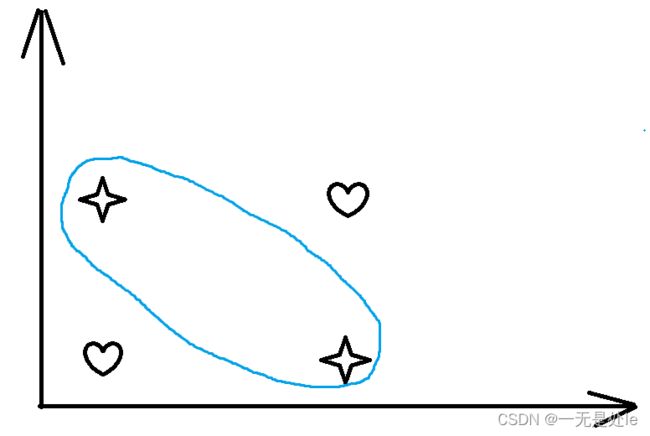
在现实生活中，我们往往会遇到的都不是一些简单的问题，通常是一些奇奇怪怪，难以解释的问题，例如线性不可分问题，该如何解决，如下图：
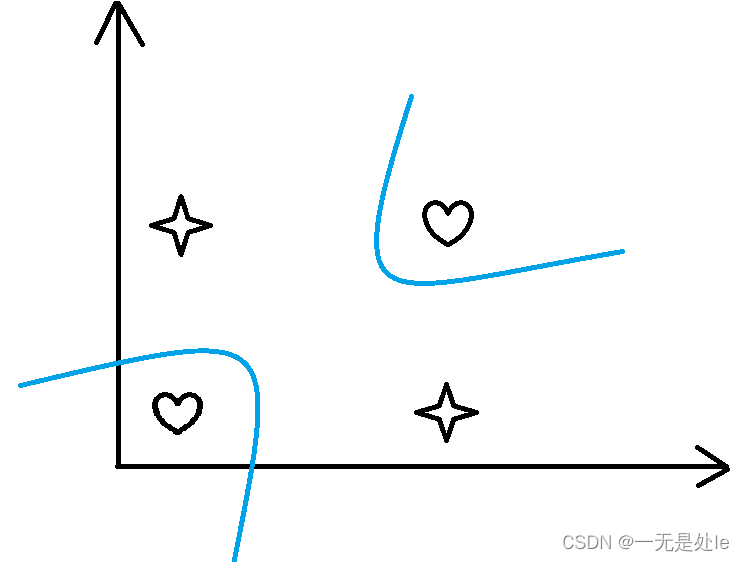
就是这么一个常见的问题（线性不可分），我们该如何对他进行分类？有人可能会想到，这用一条曲线就可以将两类分开，即多项式回归，如下图：
这样就可以完美的分开两类，但是这样必要需要引入更多的特征，那么这些特征从哪里来？
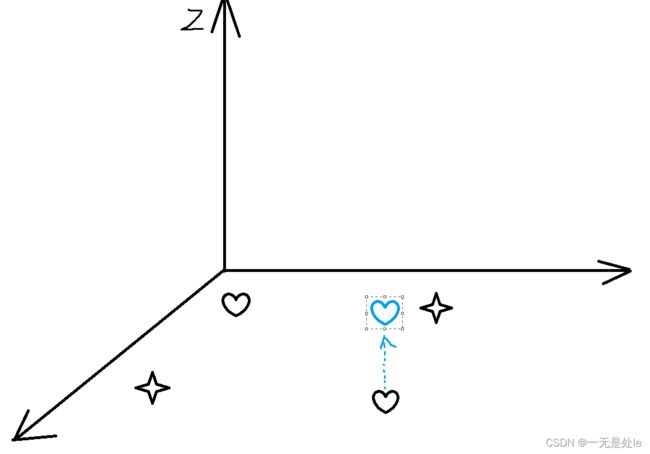
毫无疑问的，在二维坐标中我们是无法使用线性对一个线性不可分问题进行划分的。因此我们要做的就很明确了，就是需要将这两类中的一类映射到另一个维度，这样就能让线性不可分问题转化为线性可分问题。如下图：
这样就可以使用是平面划分为两类（线性） ，而且我们不需要增加特征，例如这里，原本是两个特征（x1, x2），经过映射之后还是两个特征（x1, x2, x1x2），而这样的分类结果在平面上表示如下（与上面的多项式回归本质是一样的）：
4.优化问题【重点】
不管是线性回归还是逻辑回归亦或是其他的模型，在工程上进行大数据训练的时候，哪怕使用性能再强的计算器可能都要训练很久，因此，我们需要通过一定的优化来加快训练速度。
①.数据优化
在实际的工程上，我们要求做的分类不可能是一个一个的类，大多数情况下都是一段一段的分类，因此，我们可以将数据分段化。例如广告推荐，需要针对不同年龄段的人进行不同的推广，如果按照正常的分为100类，不仅x的维度很高，要进行大量的运算，并且对于实际工程效果并没有多大的提升，因此对数据分段，根据实际情况分成相应的段数，让x变稀疏（形如[0, 0, 0, 1, 0, 0, 0....]这种矩阵虽然看似维度不变，实际很多维度不参与计算），这样能大大的加速训练过程。
②.数据预处理
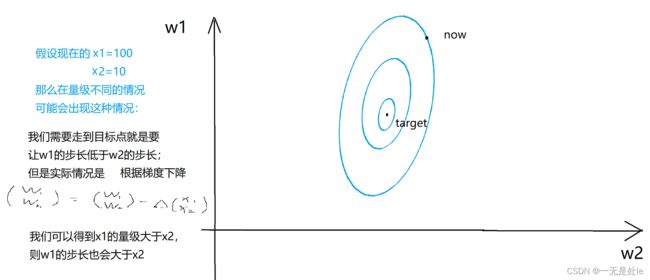
我们都知道，数据预处理是特征工程中十分重要的一个步骤，而其中最为重要的应该就是数据的标准化，因为在工程上，我们收集到的数据往往都是没有经过处理，这样的数据可能量级都不一样，这样的数据如果直接拿来使用会出现什么样的问题呢？我们看下图：
(图中的线为等高线，这里用来比较两个超参数，想了解可以自行搜索其用处，▲表示省略的微分)
图中这种冲突的情况就是输入数据量级不同带来的负面影响，这就意味着我们的模型很难（即使可以也要经过很长的时间）通过训练得到正确的答案。这就是为什么我们需要对数据进行预处理（一般都是数据标准化，有需要可以增加其他步骤），这里我们仅需要对数据进行标准化即可。
标准化的公式最简单可以使用 
进行，这样数据都会拟合到（0，1）区间，但是这个公式有一个很大的问题就是容易受到脏数据的影响，如果数据中出现了一个脏数据，所有的数据都会被污染，无法使用，例如出现了一个很大的数据，那么所有的数据经过这个标准化都会化为错误的数据，因此我们需要改进。
现在使用的标准化公式一般为 
其中 
表示均值，
表示方差。正态分布
详细参考：(2条消息) 机器学习——特征工程——数据的标准化（Z-Score,Maxmin,MaxAbs,RobustScaler,Normalizer）_robustscaler 标准化原理_xia ge tou lia的博客-CSDN博客https://blog.csdn.net/huangguohui_123/article/details/105813207?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522168941110516800226552330%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=168941110516800226552330&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-105813207-null-null.142%5Ev88%5Econtrol_2,239%5Ev2%5Einsert_chatgpt&utm_term=%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E6%95%B0%E6%8D%AE%E6%A0%87%E5%87%86%E5%8C%96&spm=1018.2226.3001.4187
③.模型优化【正则化】【重点】
当我们的模型构建好后，评估好之后，最终的需求就是需要让模型在测试集上也能有在训练集上的效果（越接近越好，一般不会出现超过训练集的情况）。那么我们的最终需求可以总结为：训练集上效果好，模型在训练集和测试集上差异小。
我们先抛开分类效果不谈，概率p=0.5的时候差异最小（此时w=0，模型完全是乱蒙），因此我们可以得出w越小，模型在训练集和测试集上的差异越小，因此得出公式：
![cost=\frac{-1}{n}\sum_{i=1}^{n}\left [y_{i}log(f_{i})+(1-y_{i})log(1-f_{i}) \right ]+\lambda ||w||](http://img.e-com-net.com/image/info8/d4b0bd3b0bd84b4a8331c4ebdc7eeb3c.png){kind=small}
在这个公式当中，![\frac{-1}{n}\sum_{i=1}^{n}\left [y_{i}log(f_{i})+(1-y_{i})log(1-f_{i}) \right ]](http://img.e-com-net.com/image/info8/eab114c348cf441584c4a0f802d72860.png){kind=small}
这一块用来调节分类器的性能，即让模型在训练集上效果好，
这一块用来衡量w的算子，即让模型在训练集和测试集上差异小，两部分相互牵制，
用来调节上面两块的比例，需要性能还是稳定。这部分的算子就是模型的正则项。这部分是逻辑回归中不可或缺的部分，因为当 为0的时候，模型只考虑训练集上的性能的情况下，模型中的w会不断变大，让函数变“硬”以达到降低损失（可以先看下面第9点），这样就会让w无限放大最后溢出，就算没溢出最终在训练集上的效果很好，但是在测试集上的效果就会很差，典型的过拟合，这样的模型不符合我们的要求。
因此我们总结一下正则项的作用：
1.从机器角度考虑：抑制w在正确分类的情况下，按比例无限增大
2.减少测试集和训练集的差异
3.破坏模型在训练集上的效果
正则项的衡量方式：
1. = 
L1正则
2. = 
L2正则
L1正则和L2正则的区别：
L1正则是直接将对整体损失函数降低贡献小（不重要）或者冗余的特征给去掉（w为0）【绝对，但能用于降维】
L2正则则是将各个特征都减小，对整体损失函数降低贡献小（不重要）或者冗余的特征的权重尽量减小（w接近于0）【更为严谨，官方库默认使用】
这两种正则项的区别其实跟上一章中的损失函数取 
和 
的区别类似，先看下图：
如图所示，我们可以发现，L1正则项对于w的改变无论什么时候对损失函数的贡献都是一样的，但是L2正则项则不同，随着w的降低，其对于损失函数的贡献就会逐渐降低。因此对于L1来说，w会一直减小直到0，而对于L2正则项来说，当w降低到一定的值之后（接近0）其对损失函数的贡献远远小于改变其他特征的w带来的贡献小，因此计算机就会转移注意力取改变其他w。
还有一个很重要的区别就是L1正则项不是处处可微的，而L2正则项处处可微，这也能在一定程度上说明上面说到的L1会使w变为0，而L2只会不断减小到接近于0。
详细理解参考：机器学习中正则化项L1和L2的直观理解_l1正则化_阿拉丁吃米粉的博客-CSDN博客https://blog.csdn.net/jinping_shi/article/details/52433975?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522168938487916800184178189%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=168938487916800184178189&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~baidu_landing_v2~default-8-52433975-null-null.142%5Ev88%5Econtrol_2,239%5Ev2%5Einsert_chatgpt&utm_term=l1%E6%AD%A3%E5%88%99%E5%8C%96%E5%92%8Cl2%E6%AD%A3%E5%88%99%E5%8C%96&spm=1018.2226.3001.4187
5.分类阈值划分问题
在实际工程上，我们不可能说像推导激活函数一样，>=0.5的为一类，<0.5的为一类，因为任何模型预测都是存在错误率的，大多数情况下我们都是需要根据需求手动调整分类的阈值。举一个例子，例如病人癌症预测问题，医院需要尽可能的不错过一个癌症患者（宁多判，不少判），如果这时候阈值设置为0.5那么就会错过很多的癌症患者（阈值设置的越低，正确率越低，后面会讲到），因此在这种情况下，医院可能会要求阈值设置在0.99或者更高，就是这个原因。
6.样本不均衡问题
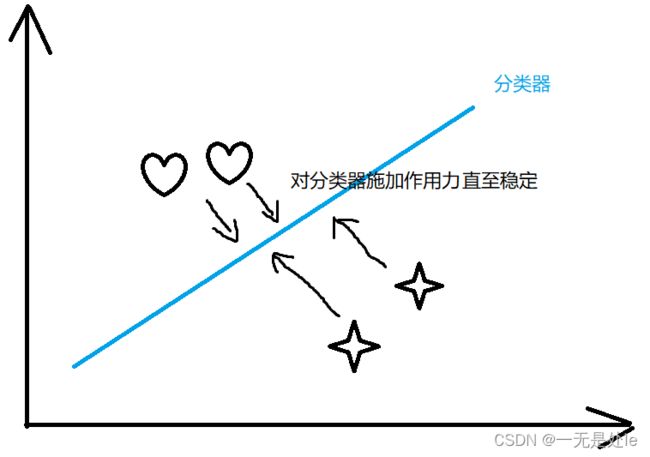
逻辑回归在训练模型，调整w的时候，其过程可以看作是每一个点都对分类器产生作用，远离分类器，如下图所示：
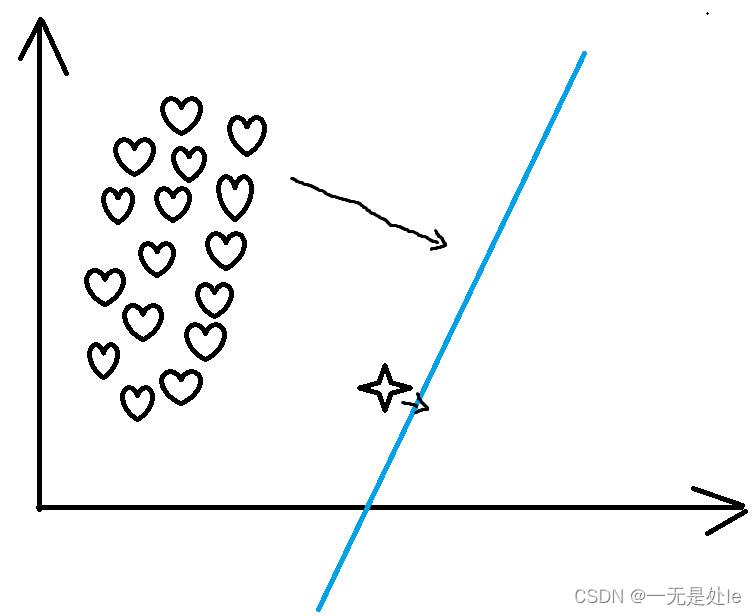
那么就有一个很明显的问题，那就是当两类的样本数量不均衡的情况下会发生什么情况？例如一类样本有9999个，另一类只有1个，出现的情况可能为如下：
按照这种情况分类，那么分类器的正确率能高达99.99%，但是没有实际的意义，这就是上面所说的样本不平衡问题（unbalanced）。那我们要解决这个问题肯定需要平衡样本，要么减少大样本的数量（下采样），要么增加小样本的数量（上采样），在实际过程中，我们一般多用上采样，因为在现实中，标注的样本较少，并且样本数减少的话对于预测效果可能会有一定的影响。那么如何进行上采样呢？实际情况下也不允许获取更多的样本的情况下，我们多使用现有的数据进行随机的重复，达到平衡样本的效果。这些数据都是真实的，只是用来平衡样本，因此不会对模型效果产生影响。
7.模型评估
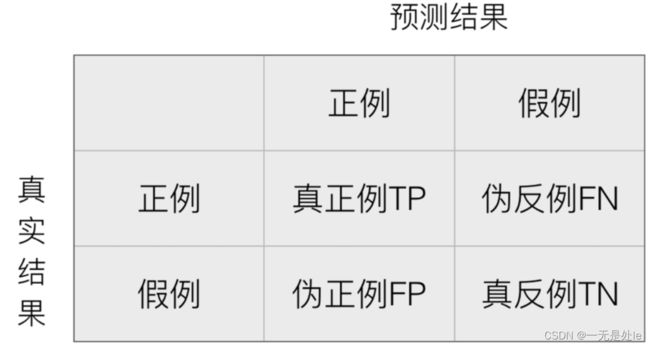
在实际工程中，我们往往会对训练好的模型进行评估，来判断其各种性能。首先我们得引入混淆矩阵，这是所有指标的评判的基础。
在分类任务下，预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合，构成混淆矩阵(适用于多分类)
这里再给出几个评估模型的指标（都是硬知识，需要记住）：
1.正确率：预测结果为所有样本中正确的比例。【范围有限且容易受到样本不均衡的影响】
计算公式为：
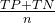
2.精确率：预测结果为正例样本中真实为正例的比例。【忽略了FN且容易受到阈值和不平衡数据集的影响】
计算公式为：
，如下图：
3.召回率：真实为正例的样本中预测结果为正例的比例（查得全，对正样本的区分能力）。【忽略了FP，与精确率成负相关】
计算公式为：
，如下图：
综合来看，上面提到的每一个评估指标如果单个拿出来看都是不能很好的评估模型的好坏，如果综合起来也会出现一些问题且不直观，因此我们需要寻找另一个更好的评估指标----AUC指标【能真正的评估模型的分类能力】。
这里先给出AUC指标的基底，
- TPR = TP / (TP + FN)【所有真实类别为1的样本中，预测类别为1的比例】
- FPR = FP / (FP + TN)【所有真实类别为0的样本中，预测类别为1的比例】
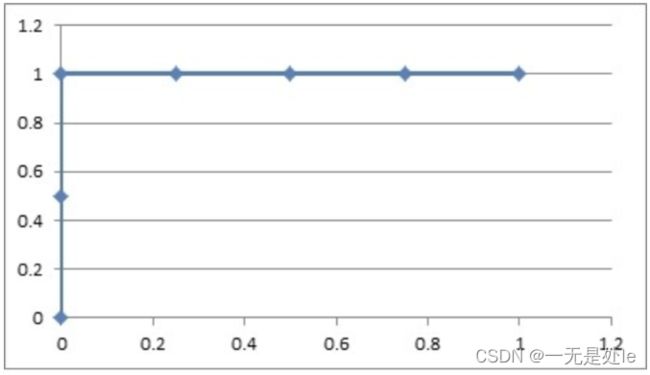
这里再给出AUC的图像ROC曲线
这么看图可能看不出什么东西，我们对他进行一定的推导：
假设有6次展示记录，有两次被点击了，得到一个展示序列（1:1,2:0,3:1,4:0,5:0,6:0），前面的表示序号，后面的表示点击（1）或没有点击（0）。
例1：如果概率的序列是（1:0.9,2:0.7,3:0.8,4:0.6,5:0.5,6:0.4），那么我们可以得到点击与否和其对应的概率的序列如下图（概率由大到小排列）：
那么我们由此可以通过计算TPR和FPR画出ROC曲线如下：
这个时候我们从得到的序列表就可以看到，我们可以通过划分阈值完美的分开两类，正样本的概率总在负样本之上，所以分对的概率为1，AUC=1。再看那个ROC曲线，它的积分是什么？也是1，ROC曲线的积分(曲线所围成的面积)与AUC相等。
例2：概率的序列是（1:0.9,2:0.8,3:0.7,4:0.6,5:0.5,6:0.4） ，那么我们可以得到点击与否和其对应的概率的序列如下图（概率由大到小排列）：
那么我们由此可以通过计算TPR和FPR画出ROC曲线如下：
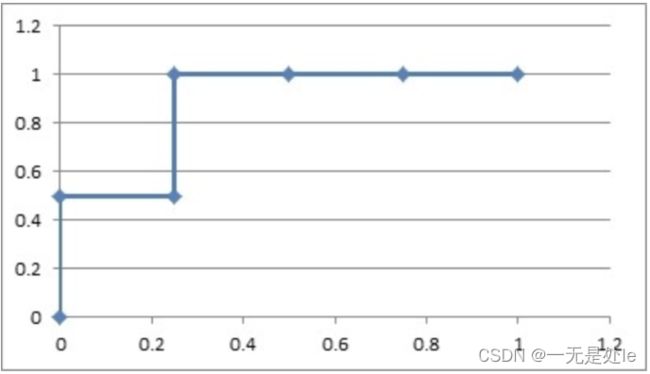这个时候我们就没法像上一个例子一样通过划分阈值完美的分开两类，如果取到了样本2和3，那就分错了，其他情况都分对了；所以分对的概率是0.875，AUC=0.875。再看那个ROC曲线，它的积分也是0.875，ROC曲线的积分与AUC相等。
例3：如果概率的序列是（1:0.4,2:0.6,3:0.5,4:0.7,5:0.8,6:0.9），那么我们可以得到点击与否和其对应的概率的序列如下图（概率由大到小排列）：
那么我们由此可以通过计算TPR和FPR画出ROC曲线如下：
这种情况下无论怎么取，都是分错的，所以分对的概率是0，AUC=0.0。再看ROC曲线，它的积分也是0.0，ROC曲线的积分与AUC相等。事实上，实际工程上是不可能出现这种情况的（不会出现正确率低于50%的情况），出现这种情况只能说明权值w取错了，只需要手动取反即可得到一个很好的分类器，之后会讲到。
经过上面的三个例子，其实我们已经对AUC和其对应的ROC曲线有了一定的了解，我们从上面的例子知道总共6个点，2个正样本，4个负样本，取一个正样本和一个负样本的情况总共有8种。任意正样本的得分大于负样本的得分的数量 / 总量 （曲线围成的面积）就是对应的AUC指标，这种指标因为考虑了所有的样本，因此可以避免阈值和不均衡样本带来的影响。
8.同模型不同权重(系数)的影响
对于同样的模型，例如x1+x2=0 这个分类模型，同样的，取
或者
即
只要a不为0，取任何数这个模型都是等价的，那么这些模型有什么区别呢？是否有好坏之分？答案是肯定的。
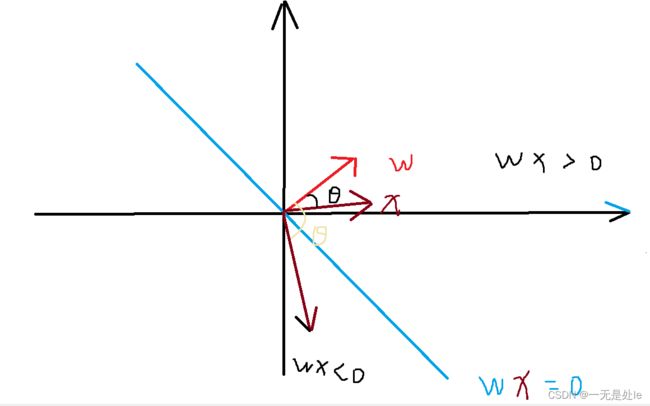
如上图所示，将分类器的权重w和自变量x看作向量，则w为分类线段的法向量，wx则为为经过归一化的内积，则x方向为w指向的方向（内积大于0）时为正类的方向，反之（内积小于0）则为负类方向。使用代数证明如下：
那么我们知道上面的性质之后，则可以知道，只要让权重w取反，就能直接改变分类器，例如一个模型的分类正确率只有30%，则仅需要w取反就可以得到70%的正确率，因此这就是上面为什么说不会存在低于50%正确率的分类器。
那么对于权重w放大会有什么样的影响呢？
9.sigmoid函数推导（为什么要用sigmoid函数）
推导过程如下：
10.KL距离推导（为什么要用KL距离作为损失函数）
推导过程如下：
总结
这是我自己对于机器学习学习笔记系列的第二章，逻辑回归，也可以看作是第一章（线性回归）的拓展，这里我只列出了我学习之后对于逻辑回归的自己的理解（要点），而代码可以自己根据理解，不使用别人封装好的库，自己来实现逻辑回归的各种公式，自己模拟实现一遍使用逻辑回归的机器学习项目。这样对于理解逻辑回归有着很大的帮助。还是那句话，这些都是我个人学习过后的理解，如有错误的地方欢迎指出。