leetcode算法之分治-归并

1.排序数组

排序数组

//分治-归并
class Solution {
    int tmp[50010];
public:
    vector<int> sortArray(vector<int>& nums) {
        mergeSort(nums,0,nums.size()-1);
        return nums;
    }

    void mergeSort(vector<int>& nums,int left,int right)
    {
        if(left>=right) return;
        //1.选择中间点划分区间
        int mid = (left+right)>>1;
        //[left,mid][mid+1,right]
        //2.将左右两区间排序
        mergeSort(nums,left,mid);
        mergeSort(nums,mid+1,right);
        //3.合并两个有序数组
        int cur1 = left,cur2 = mid+1,i=0;
        while(cur1<=mid && cur2<=right)
        {
            tmp[i++] = nums[cur1]>=nums[cur2]?nums[cur2++]:nums[cur1++];
        }
        while(cur1<=mid) tmp[i++] = nums[cur1++];
        while(cur2<=right) tmp[i++] = nums[cur2++];
        //还原
        for(int j=left;j<=right;j++)
        {
            nums[j] = tmp[j-left];
        }
    }
};

2.数组中的逆序对

数组中的逆序对

class Solution {
    int tmp[50010];
public:
    int reversePairs(vector<int>& nums) {
        return mergeSort(nums,0,nums.size()-1);
    }

    int mergeSort(vector<int>& nums,int left,int right)
    {
        if(left>=right) return 0;
        int ret = 0;
        //1.选择中间元素划分区间
        int mid = (left+right)>>1;
        //[left,mid][mid+1,right]
        //2.计算左右区间的逆序对的个数
        ret += mergeSort(nums,left,mid);
        ret += mergeSort(nums,mid+1,right);
        //3.计算一左一右逆序对的个数+合并两个有序数组
        int cur1 = left,cur2 = mid+1,i=0;
        while(cur1<=mid&& cur2<=right)//升序
        {
            if(nums[cur1]<=nums[cur2]) tmp[i++] = nums[cur1++];
            else
            {
                ret += mid-cur1+1;
                tmp[i++] = nums[cur2++];
            }
        }
        while(cur1<=mid) tmp[i++] = nums[cur1++];
        while(cur2<=right) tmp[i++] = nums[cur2++];
        //还原
        for(int j=left;j<=right;j++)
        {
            nums[j] = tmp[j-left];
        }

        return ret;
    }
};

3.计算右侧小于当前元素的个数

计算右侧小于当前元素的个数

class Solution {
    vector<int> ret;
    vector<int> index;//记录nums当前元素的原始下标

    int tmpNums[500010];
    int tmpIndex[500010];
public:
    vector<int> countSmaller(vector<int>& nums) {
        //计算当前元素之后，有多少个比我小(降序)
        int n = nums.size();
        ret.resize(n);
        index.resize(n);
        //初始化index数组
        for(int i=0;i<n;i++)
        {
            index[i] = i;
        }
        mergeSort(nums,0,n-1);
        return ret;
    }

    void mergeSort(vector<int>& nums,int left,int right)
    {
        if(left>=right) return;
        //1.选择中间元素划分区间
        int mid = (left+right)>>1;
        //[left,mid][mid+1,right]
        //2.将左右区间进行排序
        mergeSort(nums,left,mid);
        mergeSort(nums,mid+1,right);
        //3.处理一左一右的情况
        int cur1 = left,cur2 = mid+1,i=0;
        while(cur1<=mid&& cur2<=right)//降序
        {
            if(nums[cur1]<=nums[cur2])
            {
                tmpNums[i] = nums[cur2];
                tmpIndex[i++] = index[cur2++];
            }
            else
            {
                ret[index[cur1]] += right-cur2+1;
                tmpNums[i] = nums[cur1];
                tmpIndex[i++] = index[cur1++];
            }
        }
        while(cur1<=mid) 
        {
            tmpNums[i] = nums[cur1];
            tmpIndex[i++] = index[cur1++];
        }
        while(cur2<=right)
        {
            tmpNums[i] = nums[cur2];
            tmpIndex[i++] = index[cur2++];
        }
        //还原
        for(int j=left;j<=right;j++)
        {
            nums[j] = tmpNums[j-left];
            index[j] = tmpIndex[j-left];
        }
    }
};

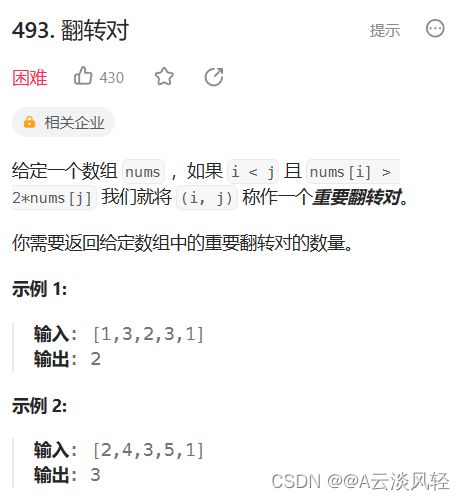
4.翻转对

翻转对

//计算当前元素之前，有多少元素的一半比我大--升序
class Solution {
    int tmp[50010];
public:
    int reversePairs(vector<int>& nums) {
      return mergeSort(nums,0,nums.size()-1);  
    }

    int mergeSort(vector<int>& nums,int left,int right)
    {
        if(left>=right) return 0;
        int ret = 0;
        //1.选择中间元素划分区间
        int mid = (left+right)>>1;
        //[left,mid][mid+1,right]
        //2.计算左右区间翻转对的个数
        ret += mergeSort(nums,left,mid);
        ret += mergeSort(nums,mid+1,right);
        //3.先计算翻转对的个数
        int cur1 = left,cur2 = mid+1,i=0;
        while(cur2<=right)//升序的情况
        {
            while(cur1<=mid && nums[cur1]/2.0<=nums[cur2]) cur1++;
            if(cur1 > mid) 
                break;
            ret += mid-cur1+1;
            cur2++;
        }
        //4.合并两个有序数组
        cur1 = left,cur2 = mid+1;
        while(cur1<=mid && cur2<=right)//升序
        {
            tmp[i++] = nums[cur1]<=nums[cur2]?nums[cur1++]:nums[cur2++];
        }
        while(cur1<=mid) tmp[i++] = nums[cur1++];
        while(cur2<=right) tmp[i++] = nums[cur2++];
        //还原
        for(int j=left;j<=right;j++)
        {
            nums[j] = tmp[j-left];
        }
        return ret;
    }
};

//计算当前元素后面，有多少元素的两倍比我小--降序
class Solution {
    int tmp[50010];
public:
    int reversePairs(vector<int>& nums) {
      return mergeSort(nums,0,nums.size()-1);  
    }

    int mergeSort(vector<int>& nums,int left,int right)
    {
        if(left>=right) return 0;
        int ret = 0;
        //1.选择中间元素划分区间
        int mid = (left+right)>>1;
        //[left,mid][mid+1,right]
        //2.计算左右区间翻转对的个数
        ret += mergeSort(nums,left,mid);
        ret += mergeSort(nums,mid+1,right);
        //3.先计算翻转对的个数
        int cur1 = left,cur2 = mid+1,i=0;
        while(cur1<=mid)//降序的情况
        {
            while(cur2<=right && nums[cur1]/2.0<=nums[cur2]) cur2++;
            if(cur2 > right) 
                break;
            ret +=right-cur2+1;
            cur1++;
        }
        //4.合并两个有序数组
        cur1 = left,cur2 = mid+1;
        while(cur1<=mid && cur2<=right)//降序
        {
            tmp[i++] = nums[cur1]<=nums[cur2]?nums[cur2++]:nums[cur1++];
        }
        while(cur1<=mid) tmp[i++] = nums[cur1++];
        while(cur2<=right) tmp[i++] = nums[cur2++];
        //还原
        for(int j=left;j<=right;j++)
        {
            nums[j] = tmp[j-left];
        }
        return ret;
    }
};