『算法笔记』- 03 - C++ 实现：双指针算法 & 位运算 & 离散化 & 区间合并

---

At first：一个初学算法的萌新，如果文中有误，还请指正
️专栏介绍：本专栏目前基于AcWing算法基础课进行笔记的记录，包括及课上大佬讲的一些算法的模板还有自己的一些心得和理解
️个人博客地址：https://blog.csdn.net/m0_73352841?spm=1010.2135.3001.5343

一、双指针算法

双指针算法是用的比较多的一种算法，其实在归并排序中，把两个区间合并的部分就应用到了双指针算法

No.1

---

双指针算法有很多种，像上面提到的这种就是一种，即在两个序列里面一个指针指向其中一个序列，另外一个指针指向另外一个序列。这是第一类，即指向两个序列

第二类是指向一个序列（更多的一种情况）。比如快速排列中，一个指针指向开头，另一个指针指向结尾，两者共同维护这一个区间

No.2

---

一般的大致写法

for (i = 0, j = 0; i < n; i ++ ) 
//整个先扫描一遍

{
	while (j < i && check(i, j )) j ++;
	//每次i更新完后更新j
	//第一个条件是j的范围，要在合法的范围内
	//第二个条件是满足某一种性质
	
	//每道题目的具体逻辑
}

核心思想：
如果是二重循环，整个的复杂度是O(n^2)

for (int i = 0; i < n; i ++ )
	for (int j = 0; j < n; j ++)

如果用双指针算法就是O(n)的复杂度。如果用两个指针扫描一个序列的话，看上去像是二重循环，但是每一个指针在所有序列里面总共用的次数是不超过n的，那两个指针总共移动的次数就是不超过2n的

所以双指针算法的核心思想就是把这样的暴力做法可以优化到O(n)。就是我们应用了某些性质，可以使得本来需要O(n^2)枚举所有情况的，变成只需要枚举O(n)个情况了

1.1 例题

No.1

题目描述
输入一个字符串，字符串开头没有空格，字符串由若干个单元组成，每个单元由若干个字符组成，每个单元之间有一个空格

请你在每行按顺序输出字符串中的每一个单元，直至输出完字符串中的所有单元

输入样例：

abc def ghi

输出样例：

abc
def
ghi

代码实现

#include 
#include 

using namespace std;

int main()
{
	char str[1000];

	gets_s(str);

	int n = strlen(str);

	for (int i = 0; i < n; i++)
	//第一个指针从0开始，一直枚举到结束为止
	//不用strlen函数第二个条件可以写成str[i]

	{
		int j = i;
		while (j < n && str[j] != ' ') j++;
		//每次循环的时候都保证指向的是单词的第一个位置
		//然后找到单词的最后一个位置
		//当循环结束的时候，j指向的是两单词之间的空格

		//这道问题的具体逻辑
		for (int k = i; k < j; k++) cout << str[k];
		

		cout << endl;

		i = j;
		//跳至下一个单词的开头

	}

	return 0;
}

No.2

题目描述
给定一个长度为n的整数序列，请找出最长的不包含重复数字的连续子序列，输出它的长度

输入格式
第一行包含整数n

第二行包含n个整数（均在0~100000范围内），表示整数序列

输出格式
共一行，包含一个整数，表示最长的不包含重复数字的连续子序列的长度

数据范围
1 <= n <= 100000

输入样例

5
1 2 2 3 5

输出样例

3

代码实现

#include 

using namespace std;

const int N = 100010;

int n;
int a[N], s[N];
//a[N]是原数组
//s[N]数组存的是当前每一个数出现的次数

int main()
{
	cin >> n;
	for (int i = 0; i < n; i ++ ) cin >> a[i];
	//读入数字

	int res = 0;
	//用res表示结果

	for (int i = 0, j = 0; i < n; i ++ )
	{
		s[a[i]] ++ ;
		//记录每次加入数出现的次数

		while (s[a[i]] > 1)
		//条件里不用写j <= i，因为当j大于i,区间没有数的时候就满足要求了。区间里一个数都没有，所以一定不会有重复的数了
		//如果新加入的数重复了，那重复的数一定是a[i]

		{
			//将指针j移到重复的那个数的边界处，即i的位置
			s[a[j]] -- ;
			j ++ ;
		}
		//结束之后i和j之间就没有重复元素了

		res = max(res, i - j + 1);
		//两个数之间的个数，在包括边界的情况下需要加1
		//比如1、2、3的个数是3-1+1
	}

	cout << res << endl;

	return 0;
}

---

1.2 图示

这里主要展示下第二个题指针移动的过程，如下图呈现

指针i，j的整个移动过程

---

二、位运算

这里主要说两种最常用的操作

No.1
一个整数n，它的二进制表示里面，第k位数是几

n=15=(1111)₂，个位是第0位，十位是第1位，以此类推

基本思路：

1、先把第k位移到最后一位，用位移，右移运算n >> k，把n的第k位数字移到个位

2、看个位是几。比方说想看下x的个位是几直接x&1就可以了，就可以把个位数取出来

把上面两步结合到一起就可以得到我们的公式：n >> k & 1。这个就是比较常用的看下n的第k位是几

实现一下

#include 

using namespace std;

int main()
{
	int n = 10;

	for (int k = 3; k >= 0; k--) cout << (n >> k & 1) ;

	return 0;
}

//输出结果为1010

---

第一次n >> k的过程

---

No.2
第二个操作，lowbit操作（同时也是树状数组的一个基本操作）。lowbit(x)返回x的最后一位1

e.g.
x=1010 lowbit(x)=10
x=101000 lowbit(x)=1000

lowbit(x)实现的时候其实就是x&(-x)，那么它为什么可以返回x的最后一位1呢？

在C++中，一个整数的负数是原数的补码（取反加1）所以-x的二进制表示是和~x+1（取反加1）的二进制表示是一样的即：x & -x = x & ( ~x + 1)

过程展示

---

lowbit(x)最基本的作用是求一下x里面1的个数

思想是每一次把它的最后一个1减掉，当x等于0的时候，里面就没有1了，减了多少次，就说明里有多少个1

2.1 例题

题目描述
给定一个长度位n的数列，请你求出数列中每个数的二进制表示中1的个数

输入格式
第一行包含整数n

第二行包含n个整数，表示整个数列

输出格式
共一行，包含n个整数，其中第i个数表示数列中的第i个数的二进制表示中1的个数

数据范围
1 <= n <= 100000，
0 <= 数列中元素的值 <= 10⁹

输入样例：

5
1 2 3 4 5

输出样例：

1 1 2 1 2

代码实现

#include 

using namespace std;

int lowbit(int x)
{
	return x & -x;
}

int main()
{
	int n;
	cin >> n;
	while (n--)
	{
		int x;
		cin >> x;

		//统计x中1的个数
		int res = 0;
		while (x) x -= lowbit(x), res ++ ;
		//当x不是0的时候，每一次就把x的最后一位1减去
		//减去多少次就说明x里面有多少个1

		cout << res << ' ';
	}

	return 0;
}

---

2.2 补充

关于原码、反码和补码

---

验证

#include 

using namespace std;

int lowbit(int x)
{
	return x & -x;
}

int main()
{
	int n = 10;
	//10的二进制表示就是1010
	
	//看下-n，转换成无符号整数
	unsigned int x = -n;
	for (int i = 31; i >= 0; i--) cout << (x >> i & 1);

	return 0;
}

//11111111111111111111111111110110，结果就是1010取反0101再加1，0110

---

为什么计算机里的负数不用反码来表示而用补码来表示？在计算机里底层实现中是没有减法的，因此就要用加法做减法

e.g.

---

三、离散化

这里特指整数、有序的离散化

假设我们有一些数值，这个数值的范围可能比较大，在0~10⁹的区间中。个数10⁵

有些题目可能需要以这些值为下标来做，那总不可能开一个10⁹的数组

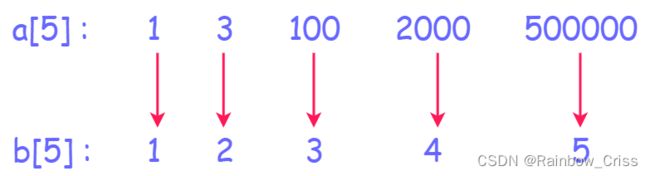
那我们可以这样来做。因为总共有10⁵ 个，把这个序列映射到从0开始连续的自然数

这个过程被称为离散化

---

问题
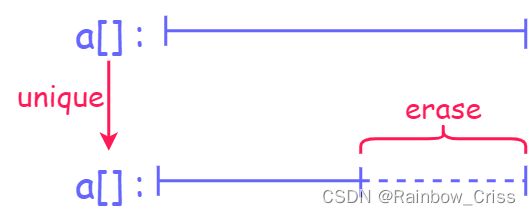
Q1、a数组中可能有重复元素，如何去重？
A1、去重的话，推荐用库函数来写：

vector<int> alls;//存储所有待离散化的值
sort(alls.begin(), alls.end());//将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());//去掉重复元素

---

unique函数将这个数组当中所有的元素去重，并且返回去重后数组的尾端点

---

Q2：如何算出a数组中每个值离散化后的值？
A2：因为a是有序（单调）的，小的一定在前面，大的一定在后面，小的一定更小，大的一定更大，那就可以用二分的方式来找

//二分求出x对应的离散化的值
int find(int x)//找到第一个大于等于x的位置
{
	while (l < r)
	{
		int mid = 1 + r >> 1;
		if (alls[mid] >= x) r = mid;
		else l = mid + 1;
	}
	return + 1;//加1从1开始映射（1、2...n），不加1从0开始映射
}

---

3.1 例题

题目描述
假定有一个无限长的数轴，数轴上每个坐标上的数都是0

现在，我们首先进行n次操作，每次操作将某一位置x上的数加c

接下来，进行m次询问，每个询问包含两个整数l和r，你需要求出区间[l, r]之间的所有数的和

输入格式
第一行包含两个整数n和m

接下来n行，每行包含两个整数x和c

再接下里m行，每行包含两个整数l和r

输出格式
共m行，每行输出一个询问中所求的区间内数字和

数据范围
-10⁹ <= x <= 10⁹，
1 <= n，m <= 10⁵，
-10⁹ <= l <= r <= 10⁹，
-10000 <= c <= 10000

输入样例：

3 3
1 2
3 6
7 5
1 3
4 6
7 8

输出样例：

8
0
5

代码实现

#include 
#include 
#include 

using namespace std;

typedef pair<int, int> PII;
//操作数

const int N = 300010;
//n操作中有一个单位，m操作中有两个单位，那就是3 * 10^5

int n, m;
int a[N], s[N];
//a[N]为存数数组
//s[N]为前缀和数组

vector<int> alls;
//存的所有要离散化的值 

vector<PII> add, query;
//操作

//求离散化后的结果
int find(int x)
{
	int l = 0, r = alls.size() - 1;
	while (l < r)
	{
		int mid = l + r >> 1;
		if (alls[mid] >= x) r = mid;
		else l = mid + 1;
	}

	return r + 1;//因为要用到前缀和所以从1开始
}

int main()
{
	cin >> n >> m;

	//读入操作
	for (int i = 0; i < n; i++)
	{
		int x, c;
		cin >> x >> c;

		add.push_back({ x, c });

		alls.push_back(x);
	}
	
	//读入操作
	for (int i = 0; i < m; i++)
	{
		int l, r;
		cin >> l >> r;
		query.push_back({ l, r });

		//把左右区间加入要离散化的数组里去
		alls.push_back(l);
		alls.push_back(r);
	}
	

	//去重
	sort(alls.begin(), alls.end());
	alls.erase(unique(alls.begin(), alls.end()), alls.end());

	//处理插入
	for (auto item : add)
	{
		int x = find(item.first);
		a[x] += item.second;//在离散化后的位置上加上要加的数
	}

	//预处理前缀和
	for (int i = 1; i <= alls.size(); i++) s[i] = s[i - 1] + a[i];
	//因为是映射到从1到alls.size()所以是小于等于

	//处理询问
	for (auto item : query)
	{
		int l = find(item.first), r = find(item.second);
		cout << s[r] - s[l - 1] << endl;
	}

	return 0;
}

---

3.2 解析

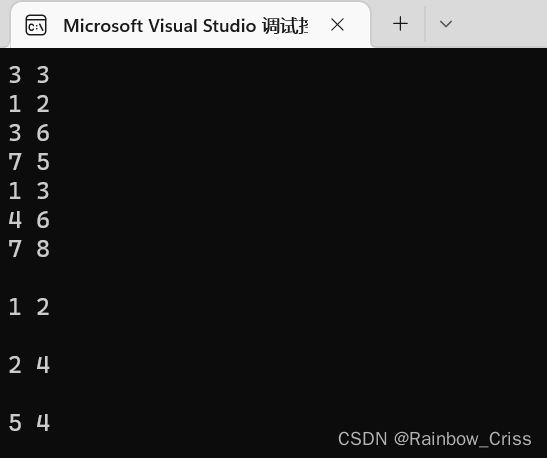
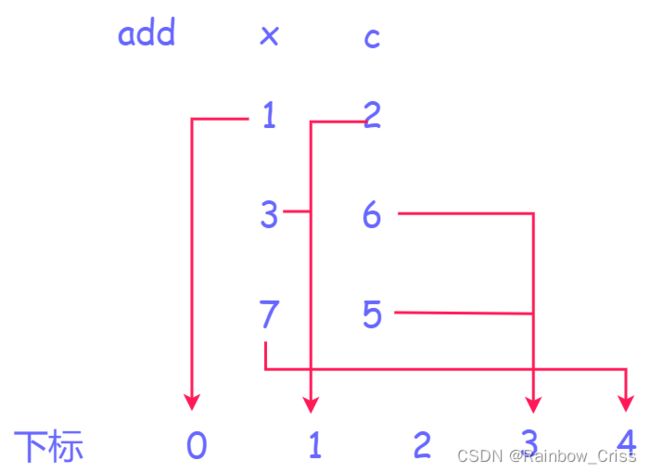
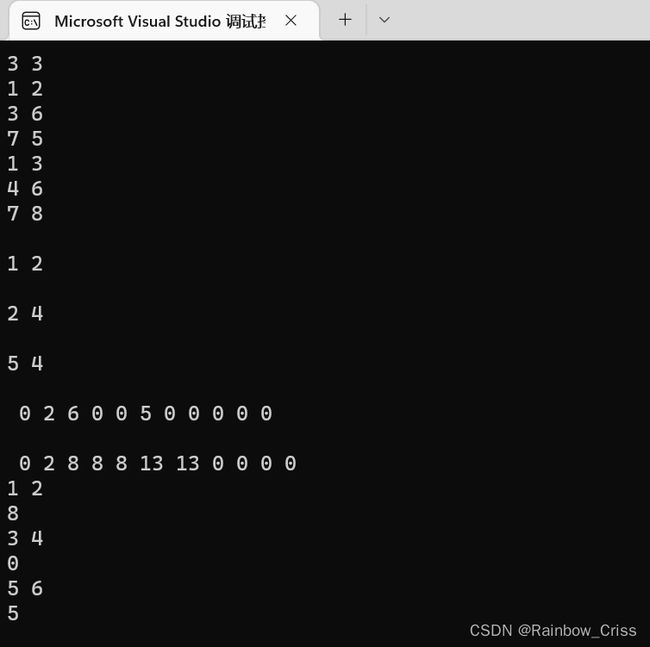
其实一开始让我迷惑的一点是，当我去打印出a数组（即离散化后的值）中的值的时候，其排列顺序并不是设想中的1->1位置，3->2位置7->3位置而是

0 2 6 0 0 5

然后我就试图去查看每一组输入x、c的位置（由于vector语法还没咋学，只能用这种笨方法qwq）然后发现其内部顺序是这样的（下面三组数是由二分找到的数，每组是该组的first和second，位置由于返回的是位置加1，所以其实际地址还需减1）

---

图示是这样的

---

可能后面再学学就知道它内部到底是咋回事了（捂脸哭.jpg）。然后是关于输入的区间l、r也是经过离散化处理的（如下图倒数第2、4、6行。输出a数组中数值的下一行是前缀和s数组中的值。8、0、5是答案）

一开始输入询问的三组区间是1、3；4、6；7、8，后来也是经过离散化处理了

---

所以对例题中代码的理解要由一个观念的转变，一开始我也在里面绕了好久

就是我一开始还拿最初的数据比如在7位置上加5对应到离散化后a数组中去比较，我说不对啊，这怎么对不上。就是这种低级的错误，因为这已经是离散化后的数据，一开始访问的区间也离散化了，就不能这样想（那会儿真是想晕了才这么蠢QAQ）

另一个是的信服这个离散化的过程，就是缩小范围，把原来的空位置抹去，我这样通过代码的转换数据一定是能得出结果的

---

附上添加测试的完整代码

#include 
#include 
#include 

using namespace std;

typedef pair<int, int> PII;

const int N = 300010;

int n, m;
int a[N], s[N];

vector<int> alls;//用来保存真实的下标和想象的下标的映射关系
vector<PII> add, query; //原来保存操作输入的值

int find(int x) {  //二分查找
    int  l = 0, r = alls.size() - 1;
    while (l < r) {
        int mid = l + r >> 1;
        if (alls[mid] >= x)
            r = mid;
        else
            l = mid + 1;
    }
    return r + 1; //  因为要求前缀和，故下标从1开始方便，不用额外的再处理边界。
}
int main() {
    cin >> n >> m;
    for (int i = 0; i < n; ++i) {
        int x, c;
        cin >> x >> c;
        add.push_back({ x, c });

        alls.push_back(x);//先把下标放入向量中 统一离散化 
    }
    for (int i = 0; i < m; ++i) {
        int l, r;
        cin >> l >> r;
        query.push_back({ l, r });

        alls.push_back(l);
        alls.push_back(r);
    }
    sort(alls.begin(), alls.end());  //排序
    alls.erase(unique(alls.begin(), alls.end()), alls.end());//去除重复元素

    

    for (auto item : add) 
    { 
        int x = find(item.first);
        printf("\n%d %d\n", find(item.first), find(item.second));

        a[x] += item.second; 
    }


    cout << endl;

    for (int i = 0; i <= 10; i++) cout << " " << a[i];

    cout << endl;


    //for(auto a:b)中b为一个容器，效果是利用a遍历并获得b容器中的每一个值，
    //但是a无法影响到b容器中的元素。
    for (int i = 1; i <= alls.size(); ++i)
    {
        s[i] = s[i - 1] + a[i];//前缀和
    }

    cout << endl;

    for (int i = 0; i <= 10; i++) cout << " " << s[i];

    cout << endl;


    for (auto item : query) {

        
        int l = find(item.first), r = find(item.second);

        printf("%d %d\n", find(item.first), find(item.second));
        cout << s[r] - s[l - 1] << endl;
    }//每个元素都对应一组{first, first}键值对（pair），
    //键值对中的第一个成员称为first，第二个成员称为second.

    


    return 0;
}

---

3.3 补充

代码实现unique函数

//unique函数的实现也是双指针算法
//unique函数返回的是一个vector的迭代器
vector<int>::iterator unique(vector<int> &a)//a数组
{
	//第一个指针遍历所有的数，第二个指针是记录下存到了第几个不同的数，同时保持条件j <= i
	int j = 0;
	for (int i = 0; i < a.size(); i++)
		if (!i || a[i] != a[i - 1])
			a[j++] = a[i];

	//a[0]至a[j - 1] 所有a中不重复的数

	return a.begin() + j;
}

---

带入题中

#include 
#include 
#include 

using namespace std;

typedef pair<int, int> PII;
//操作数

const int N = 300010;
//n操作中有一个单位，m操作中有两个单位，那就是3 * 10^5

int n, m;
int a[N], s[N];
//a[N]为存数数组
//s[N]为前缀和数组

vector<int> alls;
//存的所有要离散化的值 

vector<PII> add, query;
//操作

//求离散化后的结果
int find(int x)
{
	int l = 0, r = alls.size() - 1;
	while (l < r)
	{
		int mid = l + r >> 1;
		if (alls[mid] >= x) r = mid;
		else l = mid + 1;
	}

	return r + 1;//因为要用到前缀和所以从1开始
}

//unique函数的实现

//unique函数的实现也是双指针算法
//unique函数返回的是一个vector的迭代器
vector<int>::iterator unique(vector<int>& a)//a数组
{
	//第一个指针遍历所有的数，第二个指针是记录下存到了第几个不同的数，同时保持条件j <= i
	int j = 0;
	for (int i = 0; i < a.size(); i++)
		if (!i || a[i] != a[i - 1])
			a[j++] = a[i];

	//a[0]至a[j - 1] 所有a中不重复的数

	return a.begin() + j;
}

int main()
{
	cin >> n >> m;

	//读入操作
	for (int i = 0; i < n; i++)
	{
		int x, c;
		cin >> x >> c;

		add.push_back({ x, c });

		alls.push_back(x);
	}

	//读入操作
	for (int i = 0; i < m; i++)
	{
		int l, r;
		cin >> l >> r;
		query.push_back({ l, r });

		//把左右区间加入要离散化的数组里去
		alls.push_back(l);
		alls.push_back(r);
	}


	//去重
	sort(alls.begin(), alls.end());
	alls.erase(unique(alls), alls.end());

	//处理插入
	for (auto item : add)
	{
		int x = find(item.first);
		a[x] += item.second;//在离散化后的位置上加上要加的数
	}

	//预处理前缀和
	for (int i = 1; i <= alls.size(); i++) s[i] = s[i - 1] + a[i];
	//因为是映射到从1到alls.size()所以是小于等于

	//处理询问
	for (auto item : query)
	{
		int l = find(item.first), r = find(item.second);
		cout << s[r] - s[l - 1] << endl;
	}

	return 0;
}

---

---

四、区间合并

区间合并顾名思义，就是当两个区间有交集的时候就合并成同一个区间。当然这里有一些边界问题，我们可以特殊规定两个区间如果只有端点相交的话也算它是可以合并的

蓝色表示合并前的区间，绿色表示合并后的区间

---

解题过程

1、按照区间的左端点排序

2、扫描整个区间，扫描的过程中把所有可能有交集的区间合并

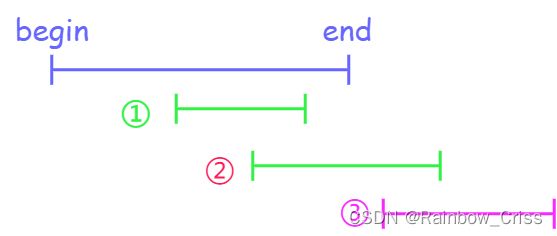
每次维护当前的一个区间，当扫描到第二个区间，第一个区间和第二个区间的关系有如下几种情况

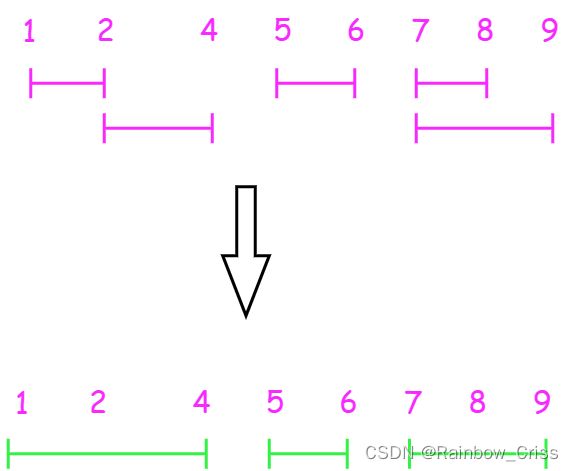
第一种情况，区间不变；第二种情况，区间延长；第三种情况，两个区间没有交集，第一个区间（蓝色）就可以放到答案中了，然后将原区间的begin和end更新到新区间（粉色）

e.g.

---

4.1 例题

题目描述
给定n个区间[ l_i, r_i ]，要求合并所有交集的区间

注意如果在端点处相交，也算有交集

输出合并完成后的区间个数

例如：[1, 3]和[2, 6]可以合并为一个区间[1, 6]

输入格式
第一行包含整数n

接下来n行，每行包含两个整数l和r

输出格式
共一行，包含一个整数，表示合并区间完成后的区间个数

数据范围
1 <= n <= 100000，
-10⁹ <= l_i <= r_i <= 10⁹

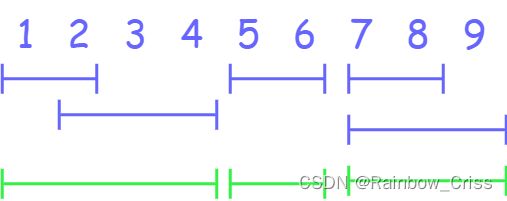
输入样例：

5
1 2
2 4
5 6
7 8
7 9

输出样例：

3

代码实现

#include 
#include 
#include 

using namespace std;

typedef pair<int, int> PII;

const int N = 100010;

int n;
//n个区间

vector<PII> segs;
//first存左端点，second存右端点

void merge(vector<PII>& segs)
{
	vector<PII> res;//存合并后的结果

	sort(segs.begin(), segs.end());//对所有区间排序

	int st = -2e9, ed = -2e9;
	//最开始还没有遍历区间，可以给一个边界值（负无穷到正无穷）
	//给的范围是10^9，给他个二倍
	
	for (auto seg : segs)
		if (ed < seg.first)//我们维护的区间严格在我们枚举的这个区间的左边
		{
			if (st != -2e9) res.push_back({st, ed});//判断一下不是初始的区间，然后放到答案里去
			st = seg.first, ed = seg.second;
		}

		//否则说明当前的区间和我们维护的区间是有交集的，那就把右端点更新成较长的
		else ed = max(ed, seg.second);
		
	//把最后的区间加入答案中去
	//防止是空的
	if (st != -2e9) res.push_back({st, ed});
}

int main()
{
	cin >> n;//区间个数

	for (int i = 0; i < n; i++)
	{
		int l, r;
		cin >> l >> r;//读入左右端点
		segs.push_back({l, r});
	}

	merge(segs);//区间合并

	cout << segs.size() << endl;

	return 0;
}

4.2 图示

过程

---

Ending