TGRS2023/遥感/目标检测：CoF-Net: A Progressive Coarse-to-Fine Framework for Object Detection

1.概述

本文提出了一种新颖的由粗到精的遥感图像目标检测框架( CoF-Net )。CoF - Net主要由两个并行分支组成，即由粗到精的特征自适应( CoF-FA )和由粗到精的样本分配( CoF-SA )，分别旨在逐步增强特征表示和选择更强的训练样本。具体来说，CoF - FA将原始的粗特征平滑地细化为具有判别性空谱细节和语义关系的多光谱非局部精细特征。同时，CoF - SA通过在训练过程中逐步引入几何和分类约束进行样本分配，动态地从粗到细考虑样本。

提出的CoF - FA以由粗到精的方式设计用于多光谱非局部特征自适应。CoF - FA在频域中显著地丰富了空谱特征细节，提高了细粒度对齐的隐式语义判别能力。

所提出的CoF - SA引入几何和分类感知约束，在训练过程中逐步动态分配样本，避免监督干扰。与CoF - FA相比，CoF - SA对遥感图像中密集和杂乱物体的准确和鲁棒定位具有重要贡献。

2.方法

2.1.整体架构

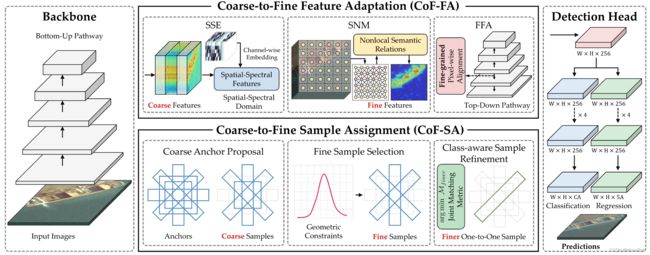
提出的CoF - Net概述。它由一个主链、一个探测头和两个关键的并行分支CoF - FA和CoF - SA组成。

所提出的CoF - Net的整体流程如图2所示。CoF - Net建立在RetinaNet [ 69 ]的基础上，是一个具有全卷积层的单阶段框架[ 78 ]，可以在少量参数的情况下实现快速推理，用于实际场景中的多尺度地理空间目标检测。

CoF - Net主要由4个部分组成：

1 ) ResNet作为CNN主干进行粗特征提取；

2 )基于FPN结构的CoF-FA ，用于增强粗略和错位特征，以自适应地生成细粒度的非局部特征，同时包含光谱和空间信息；

3 ) CoF - SA通过引入几何先验和分类约束作为选择标准，在训练过程中动态生成和提名更精细、高质量的样本，而不是简单地使用大量粗定位；

4 )检测头，由两个紧凑且并行的子网络组成，用于分类和回归以产生最终的检测结果。

通过提出的由粗到精的策略，深度特征和训练样本都得到了精化，从而提高了对遥感图像中复杂干扰的可靠性和鲁棒性，从而提升了单阶段框架的检测性能。此外，为了适应CoF - Net检测遥感图像中的旋转物体，遵循[ 1 ]，[ 21 ]，[ 32 ]和[ 50 ]，我们使用五个参数( x , y , w , h , θ)进行任意方向的矩形表示，其中θ∈[ -π / 2,0 )表示物体与x轴的锐角。此外,对于那些只涉及水平对象的数据集,如DIOR数据集和NWPU VHR - 10数据集[ 6 ]，参数θ简单地固定为任意值而不更新，形成典型的四参数表示( x , y , w , h) [ 69 ]，分别表示中心坐标、宽度和高度。

2.2.由粗到精的光谱特征自适应

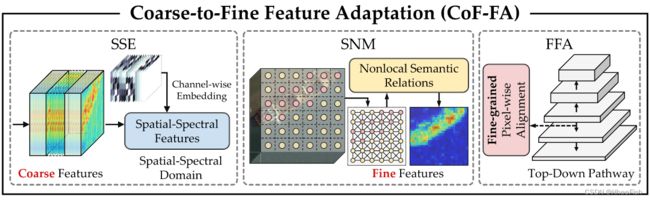
针对存在背景干扰的前景目标，为了提取更具鲁棒性和判别性的具有全局语义关系的特征，基于所提出的由粗到精的方法，提出了谱非局部特征自适应。我们的方法考虑了遥感图像中的光谱特性，并将深度特征适应于空间和频率域。如图2所示，CoF - FA由空谱嵌入( SSE )、光谱非局部调制( SNM )和细粒度特征对齐( FFA )三个模块组成，这将在本节详细阐述

2.2.1.空间-光谱嵌入Spatial–Spectral Embedding

将原始图片I输入ResNet基线会得到多尺度特征图F，但受限于CNN的感受野，提取的特征在遥感图像中易受形变和干扰。粗粒度可以由两个原因造成，仅使用空间域表示和全局语义不足。

前者激励SSE模块将光谱信息引入到空间特征中，可以增强特征的判别性和多样性。应用离散余弦变换( DCT ) [ 80 ]将粗空间特征变换到频域形成频谱特征，然后将频谱特征压缩并嵌入到粗空间特征中。一般地，给定输入的粗空间特征F(为了简洁, i被移除)，F的DCT可以写成如下形式：

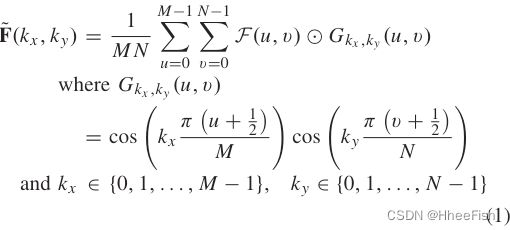
$\tilde{F}(k_x,k_y)$是F的谱表示,$G_{k_x,k_y}(u,v)$ 是二维DCT的基函数。M和N分别表示F的高度和宽度，⊙表示沿通道维度的逐元的乘法。

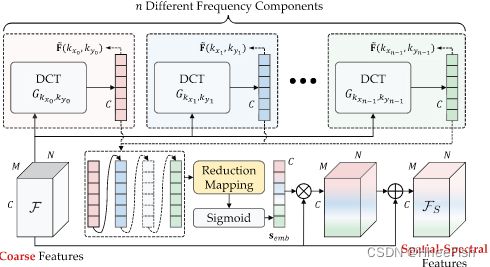
图3 .所提出的SSE模块的示意图，其中原始的粗略特征通过以通道方式嵌入多个频率成分提升为空谱特征。

为了提高目标边界响应和可区分性，在原始粗特征中嵌入多光谱信息，采用不同$k_x和k_y$ 值的基函数$G_{k_x,k_y}(\cdot )$。如图3所示，基于通道嵌入[ 56 ]，生成n个不同的频率成分，从低频到高频，并融合成原始的粗特征。具体来说，给定n个不同的DCT基$G_{k_x,k_y}$ ，由( 1 )首先推导出n个不同的光谱表示’ $\tilde{F}(k_x,k_y)$，然后计算多光谱嵌入向量：

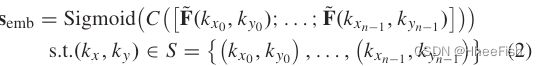
C( [ ; ])是基于一维卷积的逐通道特征级联后可学习的降维映射函数，S表示基数为| S | = n的特定组合( kx , ky)的超集。

为了进一步明确SSE模块的操作及其相对于其他方法的优势，假设( kx , ky) = ( 0、0 )且1是全1向量。那么，$G_{0,0}$= 11表示最低频率基，即零频率，我们有

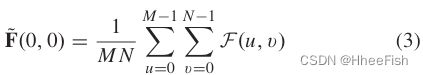
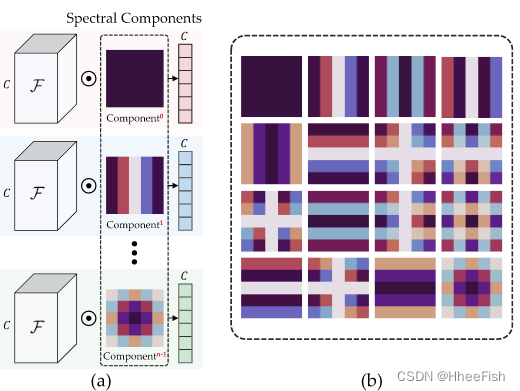
图4 . ( a )基于粗特征和不同的光谱分量，通过逐元的乘法生成多个光谱向量。( b )从低频到高频的16种不同频谱成分的可视化。

这实际上可以看作是F的全局平均池化操作，常用于[ 56 ]，[ 57 ]。然而( 3 )中只使用了零频或直流分量。该描述符潜在地消除或削弱了边界信息，仅保留了粗略的全局分布。为了弥补这一问题，如图所示。3和4 ( a )中，我们的方法利用了更多的频谱成分进行多次频率嵌入。基于相应的基频函数生成不同的光谱，如图4 ( b )所示，其中余弦基相互正交。因此，当通道多光谱嵌入向量$s_{emb}\in R^C$ 时，SSE模块的输出特征公式如下：

式中：λ∈( 0 , 1)，控制了两项的相对重要性，∂表示张量积。这样，在不增加额外计算量的情况下，所有关于物体边界的细节和关键频率信息都被聚合到空谱特征中。

2.2.2.光谱非局部调制Spectral Nonlocal Modulation

SSE模块将粗特征从空间域转换到空谱域。然而，如前所述，还存在另一个挑战，即非局部依赖关系的不足。之前的方法[ 35 ]、[ 60 ]、[ 61 ]应用简单的注意力机制来增强特征的区分度，但由于使用的卷积核的局部感受野，其性能有限。局部注意力通常是次优的，特别是对于在遥感图像中检测旋转和尺度变化的地理空间对象，因为在特征空间中建模远程依赖关系已被证明对许多计算机视觉任务至关重要[ 63 ].因此，我们引入SNM模块，通过融合短程和长程视觉依赖关系来进一步细化空谱特征，灵活构建非局部语义关系。不同于以往的空间非局部块不可避免地聚集背景噪声[ 63 ]，提出的SNM从光谱角度进行了发展和理论分析。更重要的是，在[ 66 ]和[ 81 ]的基础上，亲和矩阵被设计为对称的，以增强其稳定性，从而抑制背景噪声并提高前景区域的响应。

为了清晰起见，正则非局部算子可以统一为矩阵形式，如下文所示：

$X_F\in R^{MN\times C}$ 为F和$W_{\theta ,\phi ,g}\in R^{C\times C}$ 的空间折叠输入特征矩阵，定义为变换权重矩阵。

图5 . SNM模块的详细结构，该模块通过引入非局部上下文依赖来增强空间-光谱特征，并且仍然保留光谱特性。

具体来说，在图5中，提出的SNM模块将空谱特征$F_S\in R^{M\times N\times C}$ 作为输入，输入到3个1 × 1的卷积块中进行通道缩减和特征变换，生成3个折叠输出$X_{S;\Theta ,\Phi ,g}\in R^{MN\times C_s}$ 。然后，$X_{S;\Theta }$和 $X_{S;\Phi }$用 来生成symmetric affinity matrix对称亲和矩阵A，而$X_{S;g}$保持光谱结构上下文用于后续调制。在提出的SNM模块中，( 5 )可以实现并改写如下：

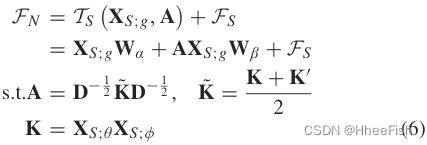
其中$T_S$ 表示光谱非局部调制器，$W_{\alpha }，W_{\beta }\in R^{C^s\times C}$ 是用于特征恢复的变换矩阵。式( 6 )计算了对称和归一化的相似度矩阵A，其中K和K’分别为成对像素相似度矩阵及其转置，D为$\tilde{K}$ 的对角度矩阵。因此，通过SNM模块，可以在相似度矩阵A中稳定地保留光谱特性，而在输出$F_N$ 中可以有效地调制非局部语义以增强其区分度 。

2.2.3.细粒度特征对齐Fine-Grained Feature Alignment

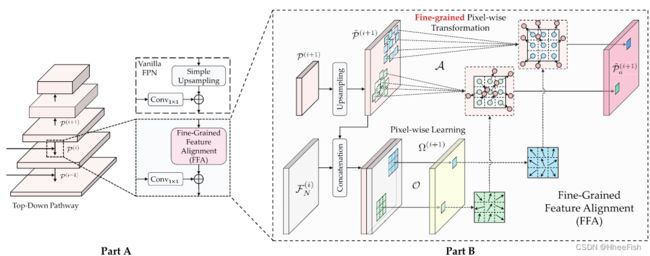
图6 .提出的FFA模块的示意图。A部分展示了基于FFA和Vanilla FPN架构的区别，而B部分描述了在细粒度像素级别对齐粗特征和细特征的详细过程

在提出SSE和SNM的基础上，有效缓解了上述由粗粒度带来的影响特征鲁棒性和区分度的两个关键问题。通过提出的渐进式特征自适应策略，来自主干的粗略特征在空间-光谱细节和语义方面都变得更精细，适合潜在的像素级操作，如对齐。在图6中，遵循典型的自底向上自顶向下构建层次特征金字塔的方案[ 36 ]，将高层特征上采样，与自顶向下路径中对应的低层特征进行聚合。然而，如果简单地采用Vanilla FPN作为颈部，可能会出现改进的精细特征和粗上采样特征之间的特征错位问题[ 82 ]。特征错位或混叠主要是由双线性插值等累积粗略和非学习的上采样操作造成的，而没有准确的对应关系，这反过来破坏了从所提出的SSE和SNM模块中生成的精化特征。为了解决这个问题，FFA模块被设计来自适应地学习一个细粒度的逐像素变换。从概念上讲，假设层次特征在自顶向下的路径上聚合后记为$P^{(i)}\in R^{M_i\times N_i\times C_i}$ ，如图6所示，一般由其更高层的特征产生，$P^{(i+1)}\in R^{(M_i/2)\times (N_i/2)\times {\hat{C}}_{i1}}$ 通过上采样产生，即$P^{(i)}=U(P^{(i+1)})+F^{(i)}$ ，其中U (·)表示常规的上采样操作。相比之下，针对其错位问题，在特征融合之前，FFA模块参考鲁棒精细特征$F_N^{(i)}$ ((2)中的输出) 中精确的空间分布和语义 ，自适应地调整和对齐$P^{(i)}$ 。FFA中用于特征对齐的操作可以表示如下：

其中${\tilde{P}}_a^{(i+1)}$ 表示对齐的上采样特征，η∈( 0 , 1)为归一化系数。具体地，如图6所示，在可学习的像素偏移${\Omega }^{(i+1)}$ 下，我们有

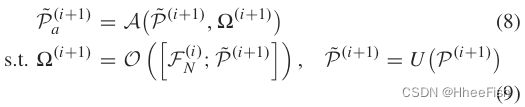
A ( · )和O ( · )分别表示基于偏移量的细粒度对齐函数和逐像素差分学习函数，由可变形卷积实现[ 83 ]，[ 84 ]，[ ;]表示级联操作以产生细$F_N^{(i)}$ 和粗’${\tilde{P}}^{(i+1)}$ 之间的空间差异。

因此，在提出的三个模块中，原始的粗特征$F^{(i)}$ 被逐步细化并适应于检测头的最终细特征$P^{(i)}$ 。这些特征对于具有复杂背景干扰和尺度变化的遥感目标检测具有更强的判别性和鲁棒性。

2.3.由粗到细的样本分配策略

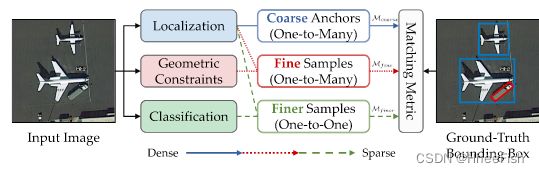
图7 .提出了CoF - SA策略的概念，该策略在粗-细-精方案中逐步分配更精确的样本用于训练。Mcoarse、Mfine和Mfiner分别表示3个渐进式匹配指标。

虽然CoF - FA阶段以由粗到精的方式成功构建了特征自适应，但对于粗训练样本，平行于粗特征表示，仍有一个问题需要解决，如图所示。1和2 .为此，本节对所提出的CoF - SA策略进行说明，简称CoF - SA，该策略在不同训练阶段动态选择更高质量的样本，以提高模型在复杂场景下的学习能力。如图7所示，遵循"粗-精-细"方案和相应的匹配度量，训练样本数量由密集变为稀疏，但监督更加精确。该过程详见算法1。CoF - SA可以分为3个顺序训练阶段，即粗略的锚点提议、通过几何约束进行精细的样本选择和更精细的对类别敏感样本精化。

2.3.1.粗锚点建议

对于大多数基于锚点的目标检测器，稠密锚点是预定义的，被确定为正负训练样本。CoF - SA在训练阶段开始时生成类别无关的粗锚点，例如在第一个Ncoarse历元中，当框架通常不能产生可靠的分类结果并且需要大量的预置锚点作为学习候选时。具体来说，基于CoF - FA中由粗到精的层次特征P ( i )，在每个层次上预先定义了多个锚点，其初始区域和尺度固定。然后，在初步训练阶段，从所有初始区域中粗略地收集正锚，并以一对多的方式分配给每个目标，只考虑位置匹配距离。给定目标的边界框t∈T*和候选锚点$a\in S_a$ ，匹配度量可以计算如下：

在实际应用中，位置距离$D_{loc}(\cdot )$ 定义为目标与所有锚点之间的交并比( IoU )，它仅基于空间位置和包围盒交集，没有考虑类别知识。

进一步，基于整个锚点集Sa和一个阈值${\epsilon }_{co}$ ，可以确定正样本如下：

式中：$a_{co}$ 表示从Sa中选取的锚。因此，所有的正样本，如( 10 )和( 11 )，在没有任何语义约束的情况下，如对象类别，在训练过程中被利用。这是一种粗略且不鲁棒的样本分配策略，只考虑遥感图像中密集的、小的地理空间对象。这样，大量的锚点存活下来，特别适合初始不成熟的训练阶段。

2.3.2.基于几何约束的精细样本选择

现有的大多数遥感目标检测器[ 14 ]、[ 30 ]、[ 85 ]都是简单地在整个训练过程采用类似的粗样本分配策略。然而，这样的静态样本分配方法是次优的。一方面，随着训练的进行，对大量训练样本进行拼接并不能提高检测精度，反而会导致无效的冗余计算。合理的做法是动态减少正样本的数量，使训练集中于具有临界区分度的竞争样本候选。另一方面，从经验上限制样本数量，如通过提高阈值ε co，并不能提升检测性能。这实际上暗示了第III - C1节介绍的类别无关IoU指导的样本分配策略的瓶颈和不足。如图所示。1和12，在训练后期，仍有大量不精确的锚点被视为正值，这可能会对密集排列的地理空间对象的检测精度产生不利影响。

对于自然场景中常见的非刚性物体，如猫、狗等，由于拍摄角度、姿态、物体形变等不同，同一类别中实例的几何特征往往不同。这导致基于IoU的度量方法在通用目标检测中占据了样本分配的主导地位，而这在遥感目标检测中是简单采用的。与俯视图中的一般视觉对象不同，地理空间目标往往是自上而下视角捕获的刚性对象，其几何属性可以作为强先验知识进行探索，但在以往的检测器中被忽略。AR对旋转和尺度变化相对不敏感，是地理空间对象最具代表性和鲁棒性的几何属性，通常符合特定的统计分布。图8给出了选取的2个Io U相同但AR不同的锚，其中AR定义为长边与短边的比值。相比于蓝色锚点，红色锚点与所考虑目标的固有AR更相似，从而捕获更具判别性的特征区域。利用AR作为几何约束可以有效减少正例的数量，使其更加精确。更重要的是，由于地理空间对象的刚性，AR通常随类别而变化，而不是随方位而变化，这明确表示了统计先验知识。因此，我们很自然地在训练阶段的中期引入这种几何约束进行精细的样本选择，以选择更精确的样本。具体来说，考虑到遥感中不同地物类别的AR相似，且在中间训练时分类性能有限，因此无需明确每个样本的具体类别。或者，根据正类的先验AR分布不同，可以将正类分为若干簇。如图9所示，有5个不同的聚类，其AR分别服从各自的统计分布。在图9中，将可能的AR切割成离散的区间，形成直方图，然后对直方图进行归一化，形成每个簇的分布。给定锚-目标对( a , t)和簇c的离散化AR KaTeX parse error: Expected 'EOF', got '}' at position 15: \tilde{AR}_a,t}̲∈Nc ，由图9 ( b )可以简单推导出先验概率$p_{a,t}^{(c)}$。然后，将几何约束定义为如下形式的交叉熵代价：

这样，经过一定周期的粗样本训练后，( 10 )和( 11 )中的样本选择标准将更新为

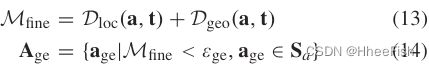
其中$M_{fine}$ 和$a_{ge}$ 分别表示更新后的匹配度量和同时受IoU和几何先验知识约束的精细样本。理论上，在( 13 )中，这样的几何约束作为先验正则项加入到样本分配度量中，有效地细化了训练样本，避免了在空间和语义不准确的样本上进行训练的困难。

2.3.3.细粒度类别感知样本精化

如上所述，在整个训练过程中，样本分配以一种渐进的粗-细-细的方式动态地分为三个阶段。为了弥合从粗粒度到细粒度的鸿沟，第二阶段利用几何先验约束来细化粗粒度样本。然而，仍有两个显著的问题亟待解决。首先，( 12 )中基于聚类的概率仅仅为样本选择提供了粗粒度的类别指导，而样本与目标之间的类别距离仍然未被发现。第二，在第一阶段和第二阶段，都需要为每个目标计算冗余和稠密的前景样本，但是在后续的训练中将这些重复的候选样本平铺为一对多的赋值是无效的。针对这两个问题，提出了一种更精细的对类别敏感一对一赋值规则，为每个潜在的候选样本选择最合适的样本。具体来说，( 13 )中的匹配度量更新为

其中，$D_{cls}(\cdot )$ 表示对类别敏感距离，用于更精细的样本赋值。在这项工作中，它被自然地定义为样本a的预测类别和t的真实类别之间的分类代价。在后面的训练阶段，网络的判别性相比之前的训练阶段有了显著的提高，使得分类更加鲁棒可靠。这揭示了为什么我们在( 12 )中采用" cluster “，而在这里采用更精细的” class "。更重要的是，一旦计算出对类别敏感匹配度量指标$M_{finer}$ ，通过搜索距离最小的正样本，可以采用更精细的一对一赋值规则：

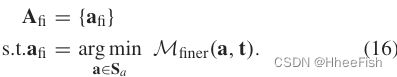
这样，只有稀疏和更细的样本被分配，而它们的近邻候选被消除。由于CoFSA以由粗到精的方式动态、渐进地引入空间位置和语义类别距离，缓解了匹配度量和损失函数之间的不一致性，从而有利于优化。此外，它在训练过程中关注最具判别性的区域，主要有利于遥感图像中密集排列和杂乱无章的目标检测。