【LGR-136-Div.4】洛谷入门赛 #11 题解

EV1.排名

题目描述

ICPC 比赛中，决定两个队排名的是通过题目数和罚时。

比较两个队排名先后的具体步骤如下：

• 首先比较两个队通过题目数。若不同，则通过数更多者排名更靠前。
• 若两队通过题目数相同，比较两个队罚时。若不同，则罚时更小者排名更靠前。
• 若通过题目数与罚时均相同，则两队排名相同。本题保证不存在这种情况。

现在给出两个队伍的通过数和罚时，你需要判断哪个队伍排名更靠前。

输入格式

输入共两行。

输入的第一行为两个整数 $A_1,P_1$，分别代表第一个队的通过数和罚时。

输入的第二行为两个整数 $A_2,P_2$，分别代表第二个队的通过数与罚时。

输出格式

输出一行一个字符串。

若第一个队排名更靠前，输出 "\n"（包含引号）。

若第二个队排名更靠前，输出 "\t"（包含引号）。

样例 #1

样例输入 #1

2 1000
1 1

样例输出 #1

"\n"

样例 #2

样例输入 #2

3 200
3 100

样例输出 #2

"\t"

提示

数据规模与约定

对于 $100\%$ 的数据，保证 $1\le A_1,A_2\le 15$，$1\le P_1,P_2\le 5000$。

---

思路

很简单的一道签到题，照着题面写一个 check 函数就行。

注意输出引号用 cout<<"\""，输出“\”用 cout<<"\\"。

code

#include 
using namespace std;
bool check(int a1,int b1,int a2,int b2){
	if(a1!=a2)	return a1>a2;
	return b1<b2;
}
int main() {
	int a1,b1,a2,b2;
	cin>>a1>>b1>>a2>>b2;
	if(check(a1,b1,a2,b2))	cout<<"\"\\n"<<"\"";
	else cout<<"\"\\t"<<"\"";
}

---

EV2.冠军

题目描述

某校举行足球比赛，将从 $16$ 强中决出冠军。
以下是 $\frac{1}{8}$ 决赛的对阵图：

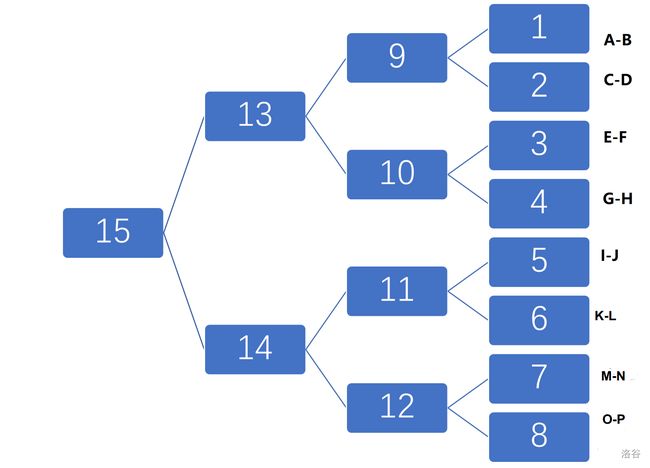
在蓝色方框中的数字代表场序数，队伍依次用字母 $\text{A}\sim \text{P}$ 编号，规定一场比赛字母更靠前的队伍为主场队伍，更靠后的队伍为客场队伍。比分用 p-q 的形式给出，$p$ 为主队的进球数，$q$ 为客队的进球数。进球更多的队伍晋级下一轮比赛。
例如，对于场序 $1$ 和 $2$，若比分分别为 $1-2$，$4-3$，则 B 队 和 C 队将晋级下一轮比赛，他们将在场序 $9$ 碰面，且 B 队为主队。
现在，按照场序顺序给出 $15$ 场比赛的比分，问冠军是哪一队？

输入格式

输入 $15$ 行，第 $i$ 行为场序 $i$ 的比分，保证比赛没有平局。

输出格式

输出一行一个字符，代表冠军队。

样例 #1

样例输入 #1

1-0
1-0
1-0
1-0
1-0
1-0
1-0
1-0
1-0
1-0
1-0
1-0
1-0
1-0
1-0

样例输出 #1

A

提示

数据规模与约定

对于 $30\%$ 的数据，$p,q\in \{0,1\}$；
对于 $100\%$ 的数据，$0\le p,q\le 100$。

提示

你可以通过下面的代码读入本题中两个整数用横线连线的格式。

scanf("%d-%d", &p, &q);

---

思路

依照树形结构打暴力，或者用队列。

这里介绍一下队列做法。

1. 先往队列里压入 A~P 。
2. 每次取出队列前两个数，比较输入的 2 个数的大小。如果 A 大压入前一个数，否则压入后一个数。
3. 直到队列里只剩下一个元素时，输出队首。

code

暴力版：

#include 
using namespace std;
char w[16];
int main(){
	for(int i=1;i<=8;i++){
		int a,b;
		char o;
		cin>>a>>o>>b;
		if(a>b)	w[i]=char('A'+i*2-2);
		else w[i]=char('A'+i*2-1);
	}
	for(int i=9;i<=12;i++){
		int a,b;
		char o;
		cin>>a>>o>>b;
		if(a>b)	w[i]=w[(i-8)*2-1];
		else w[i]=w[(i-8)*2];
	}
	for(int i=13;i<=14;i++){
		int a,b;
		char o;
		cin>>a>>o>>b;
		if(a>b)	w[i]=w[(i-12)*2+7];
		else w[i]=w[(i-12)*2+8];
	}
	int a,b;
	char o;
	cin>>a>>o>>b;
	if(a>b)	w[15]=w[13];
	else w[15]=w[14];
	cout<<w[15]<<endl;
}

队列版：

#include 
using namespace std;
queue<char> q;
int main() {
	for(int i=0;i<16;i++){
		q.push(char('A'+i));
	}
	for(int i=1,a,b;i<=15;i++){
		scanf("%d-%d",&a,&b);
		char win1=q.front();
		q.pop();
		char win2=q.front();
		q.pop();
		if(a>b)	q.push(win1);
		else	q.push(win2);
	}
	printf("%c",q.front());
}

---

EV3.扶苏与 0

题目描述

一扶苏一认为，有一些数字中，有零的影子。

如图，在数字 $2,6,9,0$ 中有一个零的影子，而在数字 $8$ 中有两个零的影子。

给出一个数，求其中零的影子的个数。

输入格式

输入一行一个整数 $X$。

输出格式

输出一行一个整数，为你的答案。

样例 #1

样例输入 #1

123456789

样例输出 #1

5

提示

数据规模与约定

对于 $20\%$ 的数据，$1\le X<10$；
对于 $60\%$ 的数据，$1\le X<10^9$；
对于 $100\%$ 的数据，$1\le X<10^{18}$。

---

思路

提前处理一个数组，表示数字 0~9 中零的个数。

输入字符串，直接查询。

code

#include 
using namespace std;
int ze[10]={1,0,1,0,0,0,1,0,2,1},ans;
int main(){
	string s;
	cin>>s;
	for(int i=0;i<s.length();i++)		ans+=ze[s[i]-'0'];
	cout<<ans;
}

---

EV4. 移植柳树

题目背景

HG 在上学的路上无聊的走着，看着这马路边的一排柳树，他的脑子里突然冒出了个奇怪的问题……

题目描述

假设总共有 $n$ 棵柳树，每一棵间隔都为 $x$。

现在他需要对这些树做一些操作，使得在「这 $n$ 棵树的起点不变」的同时，任意两棵树的间隔都为 $y$（$y>x$）。

他被允许做的操作如下；

1. 移除树木：直接删除某个位置的树木。
2. 移植树木：将一个位置的树木移到另一个位置上。

增加树木（凭空生成一棵树木）是不允许的。如果对「起点不变」这个概念有疑惑，可以参照「样例解释」中的图例。

显然操作是需要体力的，HG 想要让尽可能多的树维持原状。现在 HG 想知道，为了达成「任意两棵树的间隔都为 $y$」这个目标，他最多可以让多少棵树保持在原来的位置。

请你帮帮他吧！

输入格式

输入共一行三个整数 $n,x,y$，依次表示柳树的数量，未调整前每棵的间隔，想要达成的每棵的间隔。

输出格式

输出共一行一个整数，表示为了达成「任意两棵树的间隔都为 $y$」的目标，他最多可以让多少棵树保持在原来的位置。

样例 #1

样例输入 #1

8 2 3

样例输出 #1

3

提示

样例 1 解释

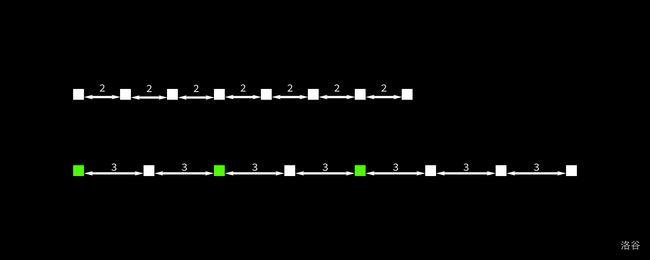
图中的方块代表树。第一行为调整前，第二行为调整后的情况。标出的三个绿色的方块是不需要移动的树，除此之外其他树都需要移动或者删除。

数据规模与约定

对于 $10\%$ 的数据，保证 $n\le 10$，$x=1$，$y=2$。
对于 $20\%$ 的数据，保证 $n\le 10^3$，且 $y$ 是 $x$ 的倍数。
对于 $100\%$ 的数据，保证 $1\le n\le 10^6$，$1\le x<y\le 10^6$。

---

思路

小学数学题

写一个 gcd 求 lcm，用总长除以 lcm，最后加上起点。

code

#include 
using namespace std;
long long gcd(long long x,long long y){
	if(x<y)	swap(x,y);
	if(y==0)	return x;
	return gcd(y,x%y);
}
int main(){
	long long a,b,c;
	cin>>a>>b>>c;
	cout<<((a-1)*b)/(b*c/gcd(b,c))+1;
}

---

HV1.移植柳树 (Hard Version)

本题与 Easy Version 题意完全相同，不同的地方仅在于数据范围和单个测试点内含有的测试组数量。

数据规模与约定

对于 $100\%$ 的数据，保证 $1\le T\le 10^5$，$1\le n\le 10^{18}$，$1\le x<y\le 10^9$。

思路

一样的方法，只不过 long long 炸了，这里我选择用 __int128 来实现。

需要注意的是，__int128 必须使用快读快写的方式读入输出。

#include 
using namespace std;
inline __int128 read(){
	char ch=getchar();
	__int128 t=1,x=0;
	while(!isdigit(ch)){
		if(ch=='-')	t=-1;
		ch=getchar();
	}
	while(isdigit(ch)){
		x=(x<<3)+(x<<1)+(ch^48);
		ch=getchar();
	}
	return x*t;
}
inline void Write(__int128 x){
	if(x>=10)	Write(x/10);
	putchar(x%10+48);
}
inline void write(__int128 x){
	if(x<0){
		putchar('-');
		x=~x+1;
	}
	Write(x);
}
__int128 ggcd(__int128 x,__int128 y){
	if(y==0)	return x;
	return ggcd(y,x%y);
}
int main(){
	__int128 T,a,b,c;
	T=read();
	while(T--){
		a=read(),b=read(),c=read();
		__int128 k=((a-1)*b)/(b*c/ggcd(b,c))+1;
		write(k);
		putchar('\n');
	}
}

---

EV5.你的牌太多了

题目描述

笨蛋扶苏和坏蛋小 F 在打一种很新的牌。

初始时，扶苏和小 F 手中各有 $n$ 张牌。每张牌有一个花色 $f$ 和一个点数 $p$。在本题中，花色是不超过 $m$ 的正整数，点数是不超过 $r$ 的正整数。

打牌共会进行 $n$ 轮，每轮扶苏会从手中选择一张牌打出。小 F 会从当前手牌中，选择与扶苏本轮打出的牌花色相同且点数大于扶苏打出的牌中点数最小的一张打出。如果这样的牌不存在，那么小 F 不会接牌（也就是不会出牌）。

注意，无论小 F 打出什么牌，本轮都立即结束，扶苏不会继续接牌，而是会开启下一轮出牌。

给出扶苏的出牌顺序，请你求出小 F 最终手里剩了几张牌。

输入格式

第一行是三个整数，表示一个人的手牌数 $n$，花色的上界 $m$ 和点数的上界 $r$。
第二行有 $n$ 个整数，第 $i$ 个整数表示扶苏第 $i$ 张牌的花色 $f{1}_i$。
第三行有 $n$ 个整数，第 $i$ 个整数表示扶苏第 $i$ 张牌的点数 $p{1}_i$。
第四行有 $n$ 个整数，第 $i$ 个整数表示小 F 第 $i$ 张牌的花色 $f{2}_i$。
第五行有 $n$ 个整数，第 $i$ 个整数表示小 F 第 $i$ 张牌的点数 $p{2}_i$。
第六行是一个长度为 $n$ 的排列，描述扶苏的出牌情况。第 $i$ 个整数 $p_i$ 表示扶苏第 $i$ 轮出了第 $p_i$ 张牌。

输出格式

输出一行一个整数，表示坏蛋小 F 结束时手里剩余的牌数。

样例 #1

样例输入 #1

3 1 2
1 1 1
1 2 1
1 1 1
2 2 1
2 3 1

样例输出 #1

1

样例 #2

样例输入 #2

3 2 2
1 2 1
1 1 1
1 2 1
2 2 2
1 2 3

样例输出 #2

0

提示

样例 1 解释

小 F 花色为 $1$ 且点数也为 $1$ 的牌管不住任何牌。其余牌都被打出去了。

数据规模与约定

• 对于 $10\%$ 的数据，$r=1$；
• 对于 $20\%$ 的数据，$n=1$；
• 对于 $50\%$ 的数据，$m=1$；
• 对于 $100\%$ 的数据，$1\le n,m,r\le 100$，$1\le f{1}_i,f{2}_i\le m$，$1\le p{1}_i,p{2}_i\le r$。$1\le p_i\le n$，$p$ 是长度为 $n$ 的排列。

---

思路

依照题意模拟即可。

code

#include 
using namespace std;
int n,m,r,p1[105],f1[105],p2[105],f2[105];
int main(){
	cin>>n>>m>>r;
	int cnt=n;
	for(int i=1;i<=n;i++)	cin>>p1[i];
	for(int i=1;i<=n;i++)	cin>>f1[i];
	for(int i=1;i<=n;i++)	cin>>p2[i];
	for(int i=1;i<=n;i++)	cin>>f2[i];
	f2[102]=0x3f3f3f3f;
	for(int i=1;i<=n;i++){
		int now,out=102;
		cin>>now;
		for(int j=1;j<=n;j++){
			if(p2[j]==p1[now]&&f2[j]>f1[now]&&f2[j]<f2[out]){
				out=j;
			}
		}//找到将要出的牌
		if(out!=102){
			cnt--;
			p2[out]=f2[out]=0;
		}//找到了
	}
	cout<<cnt;
}

---

EV6.洛谷评测机模拟器

题目背景

现在假装你是洛谷评测机。这一天，洛谷同时进行了 PION 自测、SCP 自测、ION 自测等等比赛。成千上万的评测落到了你的身上！

题目描述

现在已经知道你有 $n$ 个相同性能的评测节点，它们被分别标号为 $1,2,\cdots ,n$。一个评测节点在同一时间只能处理一个评测任务。

在某一时刻，$m$ 个评测任务同时涌入了你。我们将这些任务分别标号为 $1,2,\cdots ,m$。这些评测任务需要的评测时间分别为 $t_1,t_2,\cdots ,t_m$。每个评测任务需要且仅需要一个评测节点来运行，因此你会按照如下方式按照 $1\sim m$ 的顺序依次将这些评测任务分配到评测节点上：

对于某个耗时 $t_i$ 的评测任务，你需要找到目前累积评测时间最小的评测节点将任务放入。如果有多个评测节点累积评测时间相同且最小，则找一个标号最小的节点将任务放入。

「累积评测时间」定义：假设对于某个评测节点，其被分配了 $a_1,a_2,\cdots ,a_k$ 共 $k$ 个任务。那么这个评测节点的「累积评测时间」就是 $t_{a_1}+t_{a_2}+\cdots +t_{a_k}$。显然的，如果某个评测节点从未被分配过这 $m$ 个任务中的任何一个，那么这个评测节点的「累积评测时间」是 $0$。

现在，你需要统计出，你的这 $n$ 个评测节点分别接受了哪一些评测任务。

输入格式

输入共两行。

第一行为两个整数 $n,m$，代表评测节点数量和评测任务数量。
第二行为 $m$ 个整数 $t_1,t_2,\cdots ,t_m$，依次代表这 $m$ 个评测任务的所需时间。

输出格式

输出共 $n$ 行，每行若干个整数，两两之间以一个空格隔开。

对于第 $i$ 行，输出第 $i$ 个评测节点接受的评测任务编号从小到大排序后的结果。如果第 $i$ 个评测节点没有被分配任务，那么输出一行一个 $0$。

样例 #1

样例输入 #1

5 10
13 50 90 38 60 64 60 77 6 24

样例输出 #1

1 6
2 8
3
4 7
5 9 10

样例 #2

样例输入 #2

12 7
85 99 82 90 14 11 15

样例输出 #2

1
2
3
4
5
6
7
0
0
0
0
0

提示

数据规模与约定

对于 $100\%$ 的数据，保证 $1\le n,m\le 5\times 10^3$，$0\le t_i\le 10^9$。

测试点编号	$n\le$	$m\le$	特殊性质
$1\sim 2$	$10$	$10$	无
$3\sim 4$	$5\times 10^3$	$5\times 10^3$	$t_i=0$
$5\sim 6$	$5\times 10^3$	$5\times 10^3$	$t_i=1$
$7\sim 10$	$5\times 10^3$	$5\times 10^3$	无

---

思路

依照题意找最小值模拟，使用 vector 存储答案序列。

code

#include 
using namespace std;
long long t[5005];
vector<int> in[5005];
int main(){
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int k;
		cin>>k;
		int join=min_element(t+1,t+n+1)-t;//找最小
		t[join]+=k;
		in[join].push_back(i);
	}
	for(int i=1;i<=n;i++){
		if(in[i].size()==0)	cout<<"0";
		for(int j=0;j<in[i].size();j++){
			cout<<in[i][j]<<" ";
		}
		cout<<"\n";
	}
}

时间复杂度 $O(nm)$，对于 Easy Version 完全可以接受。

---

HV2.洛谷评测机模拟器 (Hard Version)

本题与 Easy Version 题意完全相同，不同的地方在于数据范围。

数据规模与约定

对于 $100\%$ 的数据，保证 $1\le n,m\le 5\times 10^5$，$0\le t_i\le 10^9$。

思路

很显然，$O(nm)$ 的做法在这个数据范围之下 TLE 了。

接着，我们分析一下题目。

提取出几个关键词：取最小值，维护最小值。

很明显，这就是优先队列的作用，接着，我们就可以写出优化后的算法。

code

#include 
using namespace std;
struct xi{
	long long t,num;//对应目前处理时间和编号
	friend bool operator<(xi a,xi b){
		if(a.t!=b.t)	return a.t>b.t;
		return a.num>b.num;
	}
};
priority_queue<xi> q;
vector<int> in[500005];
int main(){
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)	q.push({0,i});//初始化
	for(int i=1;i<=m;i++){
		int k;
		cin>>k;
		xi now=q.top();
		q.pop();
		now.t+=k;
		in[now.num].push_back(i);
		q.push(now);
	}
	for(int i=1;i<=n;i++){
		if(in[i].size()==0)	cout<<"0";
		for(int j=0;j<in[i].size();j++){
			cout<<in[i][j]<<" ";
		}
		cout<<"\n";
	}
}

时间复杂度 $O(m\log n)$。

---

EV7.扶苏与 1

题目背景

扶苏在 ICPC2022 EC Final 的比赛里，开局不到五分钟，就读假了一道题，把一道数位 DP 开成了简单签到，狠狠地演了队友一把。

为了不让读假了的题被浪费，所以这道题出现在了这里。

题目描述

扶苏给了你一个数字 $x$，你需要给她一个数字 $y$，使得在列竖式计算 $x+y$ 时，能恰好产生 $k$ 个进位。

你给出的 $y$ 的长度不能超过 $10^4$。

进位的含义是：在进行竖式加法运算时，如果位于同一列上的数字之和（加上低位向上可能存在的进位）比 $9$ 大，则在结果的这一列上只保留这个和的个位数字，同时称这一位向它的高位产生了一个进位。

下图是一个竖式加法的例子，结果中标红的两位都向上产生了进位。

输入格式

本题单测试点内有多组测试数据。

第一行为一个整数 $T$，代表测试数据组数。
接下来 $T$ 组数据，每组数据只有两行，每行一个整数。
第一行的整数表示 $x$。
第二行的整数表示 $k$。

输出格式

本题采用 special judge 进行判题。

对每组数据，输出一行一个整数，表示你给出的 $y$。

如果有多个满足要求的 $y$，你可以输出任何一个。但是必须保证如下三条限制：

• $y$ 是正整数。
• $y$ 不含前导 $0$。
• $y$ 的长度不超过 $10^4$。

特别的，如果这样的 $y$ 不存在，请你输出一行一个 $\text{-1}$。

样例 #1

样例输入 #1

5
1
1
14
1
514
2
1234
1
123456
6

样例输出 #1

9
8
516
7
877777

提示

数据规模与约定

• 对 $30\%$ 的数据，保证 $x<10$，$k=1$。
• 对 $70\%$ 的数据，保证 $x<10^6$。
• 对 $100\%$ 的数据，保证 $0\le x<10^{(10^3)}$，$1\le T\le 5000$，$1\le k\le 1+{\log }_{10}\max (1,x)$。输入的 $x$ 不含前导 $0$。

提示

输入的 $x$ 可能会很大。如果说 $x<10^t$，则输入 $x$ 的长度不会超过 $t$。数据规模中式子 $k \leq 1 + \log_{10}\max(1,x) $ 的含义是：$k$ 不会超过 $x$ 的长度。

---

思路

考试时因为数据太水一发过了。

对于构造进位，原数的第一位加上 $9$ 肯定能进位（除非原数为 $0$，这也是唯一无解的情况）

接着，原数第一位前一位（也就是 $0$）加上 $9$ 和第一位的进位，肯定能进位。

如果要构造 $k$ 次进位，我们只需要输出 $k$ 个 $9$，并将原数后面的位数补齐就行了。

构造出的数长度为 $k+x_{len}-1$（x为原数），不超过 $10^4$，符合要求。

code

#include 
using namespace std;
int main(){
	int T;
	cin>>T;
	while(T--){
		string s;
		int k;
		cin>>s>>k;
		if(s=="0"){
		    cout<<-1<<endl;
		    continue;
		}
		for(int i=1;i<=k;i++)	cout<<"9";
		for(int i=1;i<s.length();i++)	cout<<"0";
		cout<<endl;
	}
}

---

HV3. 扶苏与 1 (Hard Version)

题目背景

本题与 Easy Version 的区别是：$x$ 的范围不同，$y$ 的长度限制不同。

请注意 Easy Version 和 Hard Version 不是严格的包含关系。

扶苏在 ICPC2022 EC Final 的比赛里，开局不到五分钟，就读假了一道题，把一道数位 DP 开成了简单签到，狠狠地演了队友一把。

为了不让读假了的题被浪费，所以这道题出现在了这里。

题目描述

扶苏给了你一个数字 $x$，你需要给她一个数字 $y$，使得在列竖式计算 $x+y$ 时，能恰好产生 $k$ 个进位。

你给出的 $y$ 的长度不能超过 $x$ 的长度。（注意，这条要求与 Easy Version 不同）

进位的含义是：在进行竖式加法运算时，如果位于同一列上的数字之和（加上低位向上可能存在的进位）比 $9$ 大，则在结果的这一列上只保留这个和的个位数字，同时称这一位向它的高位产生了一个进位。

下图是一个竖式加法的例子，结果中标红的两位都向上产生了进位。

输入格式

本题单测试点内有多组测试数据。
第一行为一个整数 $T$，代表测试数据组数。
接下来 $T$ 组数据，每组数据只有两行，每行一个整数。
第一行的整数表示 $x$。
第二行的整数表示 $k$。

输出格式

本题采用 special judge 进行判题。

对每组数据，输出一行一个整数，表示你给出的 $y$。

如果有多个满足要求的 $y$，你可以输出任何一个。但是必须保证如下三条限制：

• $y$ 是正整数。
• $y$ 不含前导 $0$。
• $y$ 的长度不超过 $x$ 的长度。

特别的，如果这样的 $y$ 不存在，请你输出一行一个 $\text{-1}$。

样例 #1

样例输入 #1

5
1
1
14
1
514
2
1234
1
123456
6

样例输出 #1

9
8
516
7
877777

提示

数据规模与约定

对全部的测试点，保证 $0\le x<10^{(10^4)}$，$1\le T\le 5000$，$1\le k\le 1+{\log }_{10}\max (1,x)$。输入的 $x$ 不含前导 $0$。

提示

输入的 $x$ 可能会很大。如果说 $x<10^t$，则输入 $x$ 的长度不会超过 $t$。数据规模中式子 $k \leq 1 + \log_{10}\max(1,x) $ 的含义是：$k$ 不会超过 $x$ 的长度。

---

正文

ps：一道好题（自己认为）。

pps：还是第一次遇到入门赛有构造题。

好，回归主题。

题目大意

给定一个数 $a$，构造一个位数不超过 $a$ 且两者相加刚好有 $k$ 次进位的数，不存在输出 $-1$。

解题思路

首先，思考长度问题，要想能够更好的满足条件，最大进位个数越大越好，即构造字符串的长度越长越好，所以直接将构造字符串的长度定义为原字符串的长度，岂不美哉？

还是继续延续 Easy Version 的思想，从前往后扫一遍（或许从后往前也行？），能进位就进位，因为长度不会超过原字符串，很明显，这种思想的最大进位个数就是原数中的非零位。

很容易，我们就可以写出以下的错误代码：

#include 
using namespace std;
int main(){
	int T;
	cin>>T;
	while(T--){
		string s,y="";
		int k;
		cin>>s>>k;
		for(int i=0;i<s.length();i++){
			if(k!=0){
				y+=char(10-(s[i]-48)+48);	//只要进位就行，所以构造 10-s[i]。
				k--;
			}else{
				y+='0';
			}
		}
		if(!k)	cout<<y<<endl;
		else cout<<-1<<endl;
	}
}

很明显，这个代码是不能通过这道题的。

因为当遇到 $0$ 时，我们会判定其不能够进位，实际上 $0$ 却是可以进位的。

我们看到以下情况（点代表进位）：

 ... .
 300205
+199805
-------
 500010

哪怕原数只有三个非零数，却仍然有四次进位，说明我们当遇到 $0$ 时，还可以将这一位加上 $9$，并在后面构造进位，在理想状态下，这种方法最大进位次数是原数的位数。

但是，在末尾的连续零，是无法通过这种方式进位的（比如 $1023000$ 最多只能进位四次），所以还是会有无解的情况发生。

据此我们可以写出如下代码：

#include 
using namespace std;
int main(){
	int T;
	cin>>T;
	while(T--){
		string s,y="";
		int k;
		cin>>s>>k;
		for(int i=0;i<s.length();i++){
			if(s[i]=='0'){
				bool flag=1;
				for(int j=i+1;j<s.length();j++){//找非零数构造连续进位
					if(s[j]!='0'){
						if(j-i+1<=k){//判断进位个数是否超过。
							flag=0;
							k-=(j-i+1);
							for(int l=i;l<j;l++)	y+='9';
							y+=char(10-(s[j]-48)+48);
							i=j;
						}
						break;//找到非零数，连续零段结束。
					}
				}
				if(flag)	y+='0';//没找到非零数或连续零段太长。
			}else if(k!=0){
				y+=char(10-(s[i]-48)+48);			
				k--;
			}else{
				y+='0';
			}
		}
		if(k)	cout<<"-1"<<endl;
		else cout<<y<<endl;
	}
}

代码总体还有可以优化或有瑕疵的部分，希望大家多多指正。

---

EV8.写大作业

题目描述

扶苏为了写计算理论大作业已经 $36$ 小时没有合眼了。

为了能快点睡觉，扶苏找到了 $n$ 份文献，第 $i$ 份文献是一个字符串 $s_i$，她打算把这些文献组合起来。

具体来说，一共有两种操作：

• 1 x y：把文献 $s_x$ 整体拼接到 $s_y$ 的后面，然后删除 $s_x$。
• 2 x y：查询 $s_x$ 和 $s_y$ 是否相似。

我们保证在 1 x y 操作出现后，字符串 $s_x$ 不会出现在接下来的任何操作中。这就是说，操作 $1$ 至多有 $n-1$ 次。

相似的定义是：对两个字符串 $s_x$ 和 $s_y$，如果存在一种重新排列 $s_x$ 的方法，使得重排后的 $s_x$ 和 $s_y$ 相等，则称 $s_x$ 和 $s_y$ 相似。

例如，假设 $s_1=\text{ab},s_2=\text{cd},s_3=\text{abcd}$，则执行 1 1 2 后，$s_1$ 被删除，$s_2=\text{cdab},s_3=\text{abcd}$；继续执行 2 2 3 后，因为可以把 $s_2$ 重排为 $\text{abcd}$，所以 $s_2$ 和 $s_3$ 相似。

注意，操作 $2$ 不会对字符串做出实际修改。

输入格式

第一行是两个整数，分别表示文献的数量 $n$ 和操作的数量 $q$。
接下来 $n$ 行，每行一个字符串，第 $i$ 行的字符串表示 $s_i$。
接下来 $q$ 行，每行三个整数 $op,x,y$，其含义见『题目描述』。

输出格式

对个操作 $2$，输出一行一个字符串。如果 $s_x$ 和 $s_y$ 相似，则输出 $\text{Yes}$，否则输出 $\text{No}$。

样例 #1

样例输入 #1

4 4
ab
cd
abcd
abcc
1 1 2
2 2 3
2 3 4
2 2 4

样例输出 #1

Yes
No
No

提示

数据规模与约定

• 对 $30\%$ 的数据，保证 $n=2$，$q=1$。
• 对 $60\%$ 的数据，保证 $n\le 6$，$q\le 6$，$|s_i|\le 6$。
• 对 $100\%$ 的数据，保证 $2\le n\le 10^5$，$1\le q\le 10^6$，$1\le o\le 2$，$1\le x,y\le n$，且输入字符串的总长度不超过 $10^6$，输入字符串仅含小写英文字母，且不是空串。

---

思路

可以注意到字母的总数 $\le 26$，直接装桶记录每一个字符出现的个数。

合并时直接相加，判断时只需要看是否有元素不相等就行了。

code

#include 
using namespace std;
int t[100005][27];
void ion(int a,int b){
	for(int i=1;i<=26;i++)	t[b][i]+=t[a][i];
}//合并
bool check(int a,int b){
	for(int i=1;i<=26;i++){
		if(t[a][i]!=t[b][i])	return 0;
	}
	return 1;
}//判断
int main(){
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		string s;
		cin>>s;
		for(int j=0;j<s.length();j++){
			t[i][s[j]-'a'+1]++;//装桶
		}
	}
	for(int i=1;i<=m;i++){
		int opt,a,b;
		cin>>opt>>a>>b;
		if(opt==1){
			ion(a,b);
		}else{
			if(check(a,b))	cout<<"Yes\n";
			else cout<<"No\n";
		}
	}
}

---

HV4.写大作业 (Hard Version)

本题与 Easy Version 的区别在于：输入的是数列而不是字符串，输入输出格式不同，数据规模不同。

题目描述

扶苏为了写计算理论大作业已经 $36$ 小时没有合眼了。

为了能快点睡觉，扶苏找到了 $n$ 份文献，第 $i$ 份文献是一数列 $a_i$，她打算把这些文献组合起来。

具体来说，一共有两种操作：

• 1 x y：把文献 $a_x$ 整体拼接到 $a_y$ 的后面，然后删除 $a_x$。
• 2 x y：查询 $a_x$ 和 $a_y$ 是否相似。

我们保证在 1 x y 操作出现后，数列 $a_x$ 不会出现在接下来的任何操作中。这就是说，操作 $1$ 至多有 $n-1$ 次。

相似的定义是：对两个数列 $a_x$ 和 $a_y$，如果存在一种重新排列 $a_x$ 的方法，使得重排后的 $a_x$ 和 $a_y$ 相等，则称 $a_x$ 和 $a_y$ 相似。

例如，假设 $a_1=1,2$, $a_2=3,4$，$a_3=1,2,3,4$，则执行 1 1 2 后，$a_1$ 被删除，$a_2=3,4,1,2$，$s_3=1,2,3,4$；继续执行 2 2 3 后，因为可以把 $a_2$ 重排为 $1,2,3,4$，所以 $a_2$ 和 $a_3$ 相似。

注意，操作 $2$ 不会对数列做出实际修改。

输入格式

第一行是两个整数，分别表示文献的数量 $n$ 和操作的数量 $q$。
接下来 $n$ 行，每行描述一个数列。第 $i$ 行描述 $a_i$：
每行第一个数是 $m_i$，表示数列 $a_i$ 的长度，接下来有 $m_i$ 个数，描述数列 $a_i$。
接下来 $q$ 行，每行三个整数 $op,x,y$，其含义见『题目描述』。

输出格式

为了避免输出过大，请你输出一行一个整数，表示所有答案为两数列相似的询问的操作编号的按位异或和。

操作的编号从 $1$ 开始，两种操作均会令编号增加 $1$。你可以参考样例解释来理解输出格式。

样例 #1

样例输入 #1

4 5
2 1 2
2 3 4
4 1 2 3 4
4 1 2 3 3
1 1 2
2 2 3
2 3 4
2 2 4
2 3 2

样例输出 #1

7

提示

样例解释

共有五次操作，它们的编号和回答情况如下：

编号	操作	回答
$1$	1 1 2	不是查询操作
$2$	2 2 3	相似
$3$	2 3 4	不相似
$4$	2 2 4	不相似
$5$	2 2 3	相似

可以看到，回答为两数列相似的询问的操作编号为 $2$ 和 $5$。它们的按位异或和是 $7$。故输出为 $7$。

数据规模与约定

对全部的测试点，保证 $1\le n\le 10^5$，$1\le q\le 5\times 10^6$，$1\le m_i\le 10^5$，${\Sigma }_{i=1}^n{m}_i\le 5\times 10^5$。数列里的元素都是不超过 $10^9$ 的非负整数。

数据保证数列元素的生成方式是：对一个数列，限定一个该数列元素大小的上界 $k$，然后在 $[0,k]$ 内均匀随机地生成 $m_i$ 个整数作为数列 $a_i$。注意，$k$ 不一定是 $10^9$。

思路

操作 $1$ 至多有 $n-1$ 次，这是一个有用的信息，为我们后面的操作打下的基础。

这么多的查询操作次数，很容易让人想到——记忆化。

对于每一次修改操作，清空关于被修改串的所有记忆化信息。

对于每一次查询操作，如果两个串长度不等，返回 0，然后查询记忆化信息。如果没有记忆化信息，就直接比对，并更新记忆化信息。

很明显，这样的方法在极端数据下回 TLE，但是总体时间仍然在可接受的范围内。

还有另一种方法——随机 Hash。对于每一个出现过的元素赋一个随机值，将一个串内所有元素随机值的和相加。这样就可以做到在 $O(1)$的时间内合并和查询。

code

记忆化：（550ms）

#include
#define int long long
using namespace std;
inline int read(){
	char ch=getchar();
	int t=1,x=0;
	while(!isdigit(ch)){
		if(ch=='-')	t=-1;
		ch=getchar();
	}
	while(isdigit(ch)){
		x=(x<<3)+(x<<1)+(ch^48);
		ch=getchar();
	}
	return x*t;
}
inline void Write(int x){
	if(x>=10)	Write(x/10);
	putchar(x%10+48);
}
inline void write(int x){
	if(x<0){
		putchar('-');
		x=~x+1;
	}
	Write(x);
}
vector<int> t[100005];
set<int> f[100005],f2[100005];//两个记忆化，一个记录相等，一个记录不相等。
int n,m,ans;
void ion(int a,int b){
	for(int i=0;i<t[a].size();i++)	t[b].push_back(t[a][i]);//合并
	sort(t[b].begin(),t[b].end());//方便比对，先排序
	f[b].clear();
	f2[b].clear();//清空记忆化信息。
}
bool check(int a,int b){
    if(t[a].size()!=t[b].size())    return 0;
	if(f[a].count(b))   return 1;
	if(f2[a].count(b))  return 0;
	for(int i=0;i<t[a].size();i++)
		if(t[a][i]!=t[b][i]){
			f2[a].insert(b);
			return 0;
		}
	f[a].insert(b);//保存记忆化信息。
	return 1;
}
signed main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++){
		int k=read();
		for(int j=1;j<=k;j++){
			t[i].push_back(read());
		}
		sort(t[i].begin(),t[i].end());
	}
	for(int i=1;i<=m;i++){
		int opt=read(),a=read(),b=read();
		if(opt==1){
			ion(a,b);
		}else{
			if(check(a,b))	ans^=i;
		}
	}
	write(ans);
}

随机 Hash：（300ms）

#include
using namespace std;
inline int read(){
	char ch=getchar();
	int x=0;
	while(!isdigit(ch)) ch=getchar();
	while(isdigit(ch)){
		x=(x<<3)+(x<<1)+(ch^48);
		ch=getchar();
	}
	return x;
}
inline void Write(int x){
	if(x>=10)	Write(x/10);
	putchar(x%10+48);
}
inline void write(int x){
	if(x<0){
		putchar('-');
		x=~x+1;
	}
	Write(x);
}
long long v[100001];
map<int,int> m;
int main(){
	srand(time(0));
	int n=read(),q=read(),ans=0;
	for(int i=1;i<=n;i++){
		int in=read();
		for(int j=1;j<=in;j++){
			int x=read();
			if(!(m.count(x)))	m[x]=rand()*rand();
			v[i]+=m[x];
		}
	}
	for(int i=1;i<=q;i++){
		int opt=read(),x=read(),y=read();
		if(opt==1)	v[y]+=v[x],v[x]=0;
		else{
			if(v[y]==v[x])	ans^=i;
		}
	}
	write(ans);
} 

时间复杂度 $O(q+\Sigma m_i\times \log k)$（k 为值域）

---

EV9.Matrix

题目背景

Matrix 是电影《黑客帝国》的英文名称，同样也是英文名词「矩阵」。

这是一道 hack 题。在此类型的题目中，你将得到一个问题和一个解决对应问题的代码，但是给出的代码不能对于某些输入给出正确的输出。不能给出正确的输出的情况包括：

1. 输出错误的结果。
2. 运行超时。
3. 产生一些运行时未定义行为。目前技术可检测的未定义行为仅包括数组越界。

对于这一问题，你需要提交一份符合要求的输入数据，使得给定的代码不能给出正确的输出。你可以直接使用『提交答案』功能，也可以提交一份以任何语言写成的数据生成器。

---

提示：如果你使用提交答案功能，请在提交其他题目时记得将语言改回你所使用的语言。

题目描述

以下给出这道题目的叙述：

假设你处在一个 $N\times N$ 的矩阵中。矩阵左上角坐标为 $(1,1)$，右下角坐标为 $(N,N)$。矩阵中的每个位置 $(i,j)$ 都有两个权值 $a_{i,j}$，$b_{i,j}$。

我们定义两点 $(x_1,y_1)$，$(x_2,y_2)$ 之间的「距离」为曼哈顿距离，即「距离」$ = |x _ 1 - x _ 2| + |y _ 1 - y _ 2|$。

我们定义你获胜，当且仅当你处在一个位置 $(x_0,y_0)$，满足这个位置与 $(N,N)$ 间的「距离」小于等于 $2$。

初始时你处在矩阵的左上角$(1,1)$，且你手头有无限个金币。在矩阵中的每个坐标处，你可以无限次地进行如下两种操作：（假设目前你所在的坐标是 $(i,j)$）

• 花费 $a_{i,j}$ 个金币，向右移动一格（列坐标 $j$ 增加 $1$）。
• 花费 $b_{i,j}$ 个金币，向下移动一格（行坐标 $i$ 增加 $1$）。

现在你想要知道，为了获胜，你至少需要花费多少金币。

输入格式

输入共 $2N+1$ 行。

第一行为一个整数 $N$，代表矩阵的大小。
第二行至第 $N+1$ 行，每行 $N$ 个整数，其中第 $i+1$ 行第 $j$ 个整数代表 $a_{i,j}$。
第 $N+2$ 行至第 $2N+1$ 行，每行 $N$ 个整数，其中第 $N+i+1$ 行第 $j$ 个整数代表 $b_{i,j}$。

输出格式

输出一行一个整数，代表为了获胜需要花费的最小硬币数量。

样例 #1

样例输入 #1

4
1 9 2 6
4 2 8 3
2 3 2 4
2 2 3 8
9 2 8 7
1 4 6 6
2 6 5 1
8 7 3 7

样例输出 #1

10

提示

样例组与实际输入的说明

如果你直接采用『提交答案』的方式，请将输入数据命名为 1.in，并打成 zip 压缩包进行提交；

如果你采用提交数据生成器的方式，你的生成器应当输出对应的输入数据。

显然，你的程序不应该读入『输入格式』里提到的任何内容（而应该构造它们），也不应该输出『样例输出』里提到的任何内容（而是只输出你构造的输入数据）。你不应该使用样例测试你的程序，这只是对这一问题的样例说明。

数据规模要求

你给出的数据必须满足如下要求：

1. 完全符合『输入格式』的规定，不能有多余的输入，但是可以有行末空格和文末回车。
2. 数据中所有的数字都应为整数。
3. $1\le N\le 2\times 10^3$，$1\le a_i,b_i\le 100$。

目标代码

你需要 hack 如下的代码：

#include 
using namespace std;

int a[2005][2005], b[2005][2005];
int f[2005][2005], n;

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
            scanf("%d", &a[i][j]);
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
            scanf("%d", &b[i][j]);
    for (int i = 0; i <= n; ++i)
        for (int j = 0; j <= n; ++j)
            f[i][j] = 1000000000;
    f[1][1] = 0;
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j) {
            if (i == 1 && j == 1)
				continue;
			f[i][j] = min(f[i][j], f[i - 1][j] + b[i - 1][j]);
			f[i][j] = min(f[i][j], f[i][j - 1] + a[i][j - 1]);
        }
    int ans = 1000000000;
    ans = min(ans, f[n - 2][n]);
    ans = min(ans, f[n][n - 2]);
    ans = min(ans, f[n - 1][n - 1]);
    printf("%d\n", ans);
    return 0;
}

目标代码的编译选项为 -std=c++14 -fno-asm -O2。编译器为洛谷提供的 g++。你可以在『在线 IDE』中选择 C++14 语言来获得完全相同的编译环境。

判分说明

本题共一个测试点，对应唯一一个问题，hack 成功则对应测试点返回 accepted。

数据判定

你给出的数据必须完全符合『数据规模要求』，否则将得到 Unaccepted 的结果。

超时判定

程序每执行若干条指令，我们会检测一遍程序的运行时间。我们保证两次检测之间的指令条数是一个输入规模无关的量，也即每执行 $O(1)$ 条指令会进行一次检测。且两次检测之间的指令条数不会太多，一般不超过 $100$ 条 C++ 语句。

如果程序的运行时间超过 $500\text{ms}$，则判定为程序运行超时，返回 accepted 结果。

结果错误判定

如果程序在规定的时间内结束且给出了一个输出，我们会比较这个输出和完全正确的输出，如果二者不同，则判定为 hack 成功，返回 accepted 结果。

未定义行为判定

我们会在每次显式的调用数组元素前判断数组下标是否超过数组范围，如果超过，则判定为 hack 成功，返回 accepted 结果。

这就是说，如果你希望通过未定义行为进行 hack，只能对显式的调用数组元素的行为进行 hack。

样例程序

如果你使用『提交答案』功能，请务必保证打开压缩包后能且仅能直接看到一个 .in 文件。这就是说，文件结构必须是：

ans.zip
 |---1.in

这一个文件不应该被额外的文件夹包含，即文件结构不能是：

ans.zip
 |---ans(folder)
      |---1.in

关于评测信息的说明

如果 hack 成功，对应测试点的信息为 accepted。如果返回其他信息，说明程序本身有误。

例如，如果返回 TLE，不代表成功的将对应程序 hack 至超时，而是表示数据生成器本身运行超时，测试点不得分。

特别的，返回 UKE 结果可能是数据不合法（有多余内容、缺少内容或数据范围不符合要求）。

---

思路

注意看这三行代码。

ans = min(ans, f[n - 2][n]);
ans = min(ans, f[n][n - 2]);
ans = min(ans, f[n - 1][n - 1]);

注意看数据范围。
$1\le N\le 2\times 10^3$
很明显，我们应该知道要怎么做了。

code

#include 
using namespace std;
int main() {
	cout<<"1\n114514\n1919810";
}

显然的，当 $n=1$ 时数组调用越界了（虽然我在小熊猫和 Dev 和洛谷 IDE 上都运行出了结果）