C++实现树 - 02 二叉树
数据结构与算法专栏 —— C++实现
写在前面:
这一讲我们来看看二叉树的实现,还不清楚树的结构的小伙伴建议先看看上面一讲关于树的定义。
二叉树的定义
二叉树是每个结点最多有两个子树的树结构。也就是说二叉树不允许存在度大于2的树。它有五种最基本的形态:二叉树可以是空集。根可以有空的左自树或者右子树;或者左右子树都是空。其中只有左子树或者右子树的叫做斜树。

二叉树的主要性质
| 性质 | 结论 |
|---|---|
| 性质一 | 在二叉树的 i 层上至多有 2 ^ ( i - 1 ) 个结点( i >= 1 ) |
| 性质二 | 深度为 k 的二叉树至多有 2 ^ ( k ) - 1 个结点( i >= 1 ) |
| 性质三 | 在⼀棵⼆叉树中,除了叶子结点(度为0)之外,就剩下度为 2(n2) 和 1(n1) 的结点了。则树的结点总数为 T = n0 + n1 + n2 ;在二叉树中结点总数为 T ,⽽连线数为 T-1 。所以有: n0 + n1 + n2 - 1 = 2*n2 + n1 ;最后得到 n0 = n2 + 1 |
| 性质四 | 具有 n 个结点的完全二叉树的深度为 [log2n] + 1 向下取整 |
| 性质五 | 如果有⼀棵有 n 个结点的完全⼆叉树(其深度为 [log2n] + 1,向下取整)的结点按层次序编号(从第 1 层到第 [log2n] + 1 ,向下取整层,每层从左到右),则对任⼀结点 i(1 <= i <= n)有。①如果 i = 1,则结点 i 是⼆叉树的根,⽆双亲;如果 i > 1,则其双亲是结点 [i / 2],向下取整。②如果 2i > n 则结点 i ⽆左孩⼦,否则其左孩⼦是结点 2i 。③如果 2i + 1 > n 则结点⽆右孩⼦,否则其右孩⼦是结点 2i + 1 |
满二叉树
满二叉树要求所有的分支结点都存在左右子树,并且所有的叶结点都在同一层上,若满二叉树的层数为 n ,则结点数量为 2n-1 个结点,子叶只能出现在最后⼀层,内部结点的度都为 2 ,如图所示。

完全二叉树
完全二叉树与满二叉树略有不同,它的生成必须遵循从上到下,从左到右,因此我们也可以为树中的结点进行编号。通俗点来讲,就是当结点的度为 0 时或为 2 时都无关紧要,但是当结点的度为 1 时,它只能拥有左子树。

顺序存储结构
所以我们可以利用完全二叉树的特性,快速访问到对应的结点。例如编号为 k 的结点,它左孩子的编号为 2k ,右孩子的编号为 2k + 1 ,例如下图所示:

对于这种特点,我们可以用数组来顺序存储完全二叉树中的元素,通过下标可以直接访问结点的左右孩子:



这看起来访问时似乎非常方便,但是当树成斜树的时候就会出现空间资源的浪费,因为所有结点一条连下来,每个结点的左右指针中都有指向空的。
链式存储结构
结构体定义
链式存储的定义也十分的简洁,结点就保存一个数据和两个指针即左右指针。唯一有些不便的是,这样子的结构如果想要从孩子结点访问父结点需要从头遍历,当然可以在定义时多加一个指向父结点的指针。但是我们这里只讲左右指针的代码实现,方便大家理解一些。

//树的结点的结构体定义
struct tree_node {
int data;
tree_node* left_child;
tree_node* right_child;
};
初始化根结点
//初始化根结点
void init_root(int key)
{
root = new tree_node;
root->data = key;
root->left_child = root->right_child = NULL;
}
插入结点
//查找结点的位置,将temp临时指针指向要查找的结点
void find_node(int parent, tree_node* node)
{
if (node->data == parent)
{
temp = node;
return;
}
else
{
if (node->left_child != NULL)
{
find_node(parent, node->left_child);
}
if (node->right_child != NULL)
{
find_node(parent, node->right_child);
}
}
}
//插入孩子(选择一个结点插入)
void insert_child(int key, int parent)
{
find_node(parent, root); //找到要插入结点的位置,temp指向该查找结点
//如果插入结点的左指针为空,先插入到左指针中
if (temp->left_child == NULL)
{
tree_node* new_node = new tree_node;
new_node->data = key;
temp->left_child = new_node;
new_node->left_child = new_node->right_child = NULL;
}
//如果左指针已经有结点了,判断右指针是否为空
else if (temp->right_child == NULL)
{
tree_node* new_node = new tree_node;
new_node->data = key;
temp->right_child = new_node;
new_node->left_child = new_node->right_child = NULL;
}
else
{
cout << "所属父节点孩子数已满" << endl;
}
}
结点的遍历
遍历分为 4 种情况,分别是前序、中序、后序和层序遍历。要注意的是前三种遍历其实非常类似,但是第一次接触的时候需要一段时间去理解,如果花了很多时间才弄明白其实是非常正常的,这和之前写代码的思维有所不同,这里涉及到了递归思想。
其实前三种遍历的区别就在于根结点的位置,前序就优先输出根结点,中序就第二个输出根结点,后序就第三个输出根结点,下面看具体讲解。
前序遍历
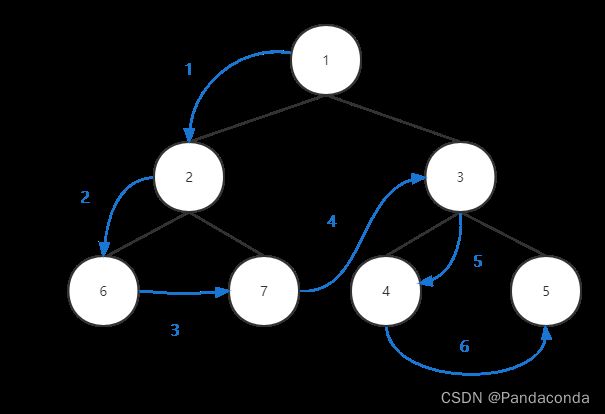
我们可以将整个树分为三个部分,分别是左子树、根结点和右子树,在写这三种遍历时我们只用取看这三个部分的位置。前序遍历顾名思义就是将根结点放到最先输出,然后再输出左子树,最后输出右子树。
(1)可以看到结果,先输出的是 1 ,其次是 1 的左右子树的值(这里我划分了颜色方便大家理解)。
(2)而 1 的左右子树又可以具体去划分,先看 1 的左子树,左子树的根结点是 2 ,所以先输出 2 这个根结点,然后再输出它的左右子树,但是此时它的左右子树只有一个值了,所以就分别输出 6 和 7 。
(3)最后再来看看 1 的右子树,3 是根结点所以就先输出,然后输出它的左右子树 4 和 5 。
总结一下,前序遍历我们先去输出它的根结点,然后再通过递归去遍历它的左子树,然后输出左子树的根结点再通过递归去遍历左子树的左子树,一直往下直到没有左子树了。最后再从最后的左子树回溯,分别去递归遍历右子树。

//前序遍历
void show_tree(tree_node *node) {
if (node == NULL)
return;
cout << node->data << " ";
show_tree(node->left_child);
show_tree(node->right_child);
}
中序遍历
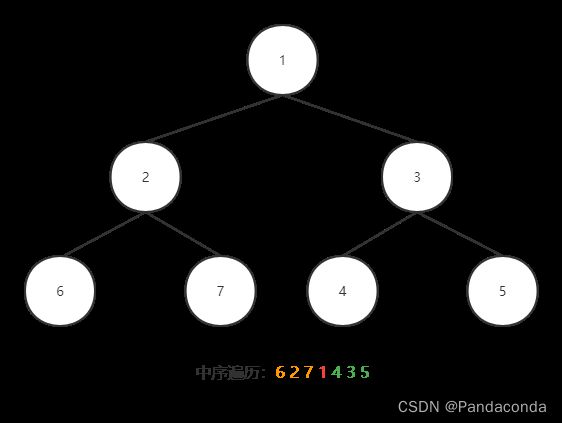
中序遍历和前序的区别是先输出根结点的左子树,再输出根结点,最后输出右子树。

//中序遍历
void show_tree(tree_node *node) {
if (node == NULL)
return;
show_tree(node->left_child);
cout << node->data << " ";
show_tree(node->right_child);
}
后序遍历
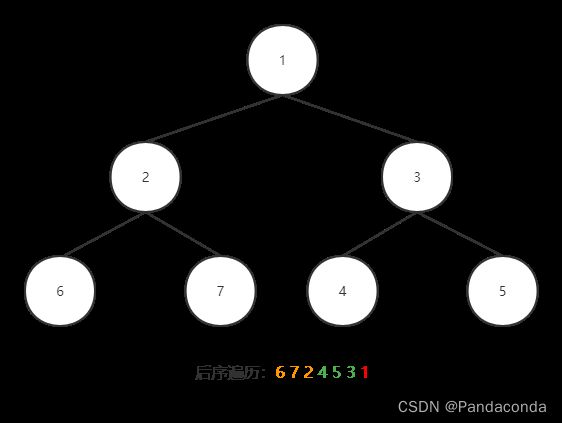
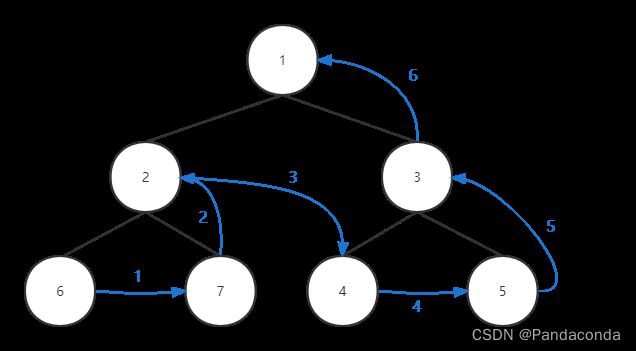
后序遍历跟前面的区别是先输出左子树,再输出右子树,最后输出根结点。其实这三种方法看下来,不光是只用改变根结点的位置,代码上也十分的简洁,三种方法代码的区别就是打印根结点的位置不同。
//后序遍历
void show_tree(tree_node *node) {
if (node == NULL)
return;
show_tree(node->left_child);
show_tree(node->right_child);
cout << node->data << " ";
}
层序遍历
层序遍历要比上面三种方法好理解一些,就是按照完全二叉树的编号顺序从上到下,从左到右遍历整棵树。
另外,由于之前我们已经对队列进行代码实现了,所以为了方便大家理解并且简化代码,我们这里就调用 STL 中的 queue 进行操作,下面实现的方法是我们比较常用的迭代法。

/*
queue.empty():判断队列是否为空,为空返回1,不为空返回0
queue.front():返回队列的首元素
queue.push():将元素推入队列的尾部
queue.pop():删除队列的尾元素
*/
//顺序遍历二叉树(从上至下,从左至右)
void show_orderly() {
queue<tree_node *> node_queue;
node_queue.push(root); //先将根结点推入队列
//只要队列不为空,就继续遍历
while (!node_queue.empty()) {
temp = node_queue.front(); //将队列的头结点取出
node_queue.pop();
cout << temp->data << " "; //输出头结点的值
//将头结点的左右子树推入队列(如果为空,则不推入)
if (temp->left_child != NULL)
node_queue.push(temp->left_child);
if (temp->right_child != NULL)
node_queue.push(temp->right_child);
}
cout << endl;
}
【扩展 - 递归法】
下面的展现方式为核心代码模式,其中用到了 STL 中的 vector 进行操作。
class Solution {
public:
void order(TreeNode* cur, vector<vector<int>>& result, int depth)
{
if (cur == nullptr) return;
if (result.size() == depth) result.push_back(vector<int>());
result[depth].push_back(cur->val);
order(cur->left, result, depth + 1);
order(cur->right, result, depth + 1);
}
vector<vector<int>> show_orderly(TreeNode* root) {
vector<vector<int>> result;
int depth = 0;
order(root, result, depth);
return result;
}
};
全部代码
#include 如果大家有什么问题的话,欢迎在下方评论区进行讨论哦~
【上一讲】树 - 01 树的三种表示法
【下一讲】树 - 03 二叉排序树