机器学习算法——集成学习1（个体与集成）
集成学习（Ensemble Learning）通过构建并结合多个学习器来完成学习任务。
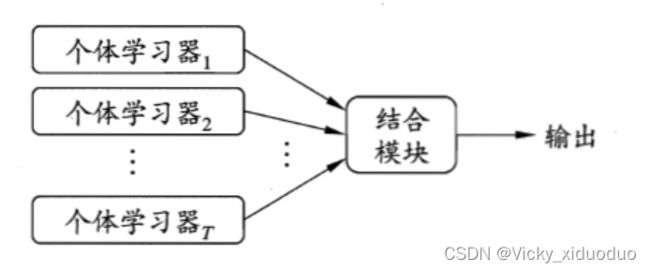
上图为集成学习的一般结构：先产生一组“个体学习器”，再用某种策略将它们结合起来。
个体学习器通常由一个现有的学习算法从训练数据产生。如C4.5决策树算法、BP神经网络等。
集成中只包含同种类型的个体学习器，例如“决策树集成”中全是决策树，“神经网络集成”中全是神经网络，这样的集成是“同质”的。
同质集成中的个体学习也称为“基学习器”，相应的学习算法称为“基学习算法”。
集成中也可以包含不同类型的个体学习器，例如同时包含决策树和神经网络，这样的集成是“异质”的。
异质集成中的个体学习器由不同的学习算法生成，这时就不再有基学习算法；相应的，个体学习器一般不称为基学习器，常称为“组件学习器”或直接称为个体学习器。
集成学习通过将多个学习器进行组合，常可获得比单一学习器显著优越的泛化性能。
那如何获得比单一学习器更好的性能呢？
比如上述这个例子：集成学习通过投票法（voting）产生，即“少数服从多数”。 （hi是分类器）
图（a），每个分类器只有66.6%的精度，但集成学习达到了100%；
图（b），三个分类器没有差别。集成后性能没有提高；
图（c），每个分类器的精度只有33.3%，集成学习的结果变得更糟。
得出：要获得好的集成，个体学习器应“好而不同”。即个体学习器有一定的“准确性”，即学习器不能太坏，并且要有“多样性”，即学习器间要具有差异。
考虑二分类问题
和真实函数f，假定基分类器的错误率为
，即每个基分类器
有：
假定集成通过简单投票法结合T个分类器，若有超过半数的基分类器正确，则集成分类就正确：
假设基分类器的错误率相互独立，则由Hoeffding不等式可知，集成的错误率为：
之后接着进行推导，设X为T个基分类器正确分类的次数，xi为单个分类器分类正确的次数。
则
，所以 
（因为假设上注明：超半数分类正确，不超半数即为分类错误）
由Hoeffding不等式可知：
则将上式变化为：
![p[\frac{1}{T}\sum_{i=1}^{T}x_i - \frac{1}{T}\sum_{i=1}^TE(x_i)\leqslant -\frac{1}{2}(1-2\varepsilon)]](http://img.e-com-net.com/image/info8/61c5b7dccdca4cda8b58cd65d8293f87.png){kind=small}
令m=T, 
，则
上式可以得出，随着集成中个体分类数目T的增大，集成的错误率将指数级下降，最终趋于零。
然而需要注意：上面有一个关键假设：基学习器的误差相互独立。在现实任务中，个体学习分类器是为解决同一个问题训练出来的，它们显然不可能相互独立。而且一般的，准确率很高以后，要增加多样性就要牺牲准确性。
事实上，如何产生并结合“好而不同”的个体学习器，恰是集成学习研究的核心。
根据个体学习器的生成方式，目前的集成学习方法大致分为两类：
一：个体学习器间存在强依赖关系，必须串行生成的序列化方法（代表：Boosting）
二：个体学习器间不存在强依赖关系，可同时生成的并行化方法（代表：Bagging和随机森林）