算法总结Golang版

【刷题】

一、一维数组

数据结构及操作函数

基本全用切片不用数组

1. 切片声明

var n []T
n := make([]T,0)
n := []T{}

2. 常用函数
   添加操作：append

	s1 := make([]int,2,4)
	s1 = append(s1,1)
	s1 = append(s1,1,2)
	
	s2 := make([]int,0,4)
	s2 = append(s2, s1...) /将s1全部追加给说s2
	s2 = append(s2, s1[0:2]...) /注意s1[0:2]仍然是个切片

拷贝操作：copy（必须声明需要拷贝的数组长度）

	dst := make([]int,len(src))
	copy(dst,src)
	copy(dst[1:],src)

删除操作：src[a:b] 【左闭右开)
遍历数组：forr fori

	s := []int{}
	for index, v := range s {}
	for i := 0; i < len(s); i++ {}

sort包操作：

import "sort"   升序

/排序
sort.Ints(x []int)
sort.Float64s(x []float64)
sort.Strings(x []string)

/ 自定义排序
sort.Slice(src,func(i, j int) bool{
	return src[i] > src[j] 逆序
})

/ 二分查找：
1. 返回x在a中的最小下标！
2. 如果x中不存在a，则返回a在x中应该存在的位置
	eg:[1,3] 中查找2则返回1;查找4则返回2（可能返回n）
 index: 0 1
	    
func SearchInts(a []int, x int) int {}
func SearchFloat64s(a []float64, x float64) int {}
func SearchStrings(a []string, x string) int {}

思路

1. 查找：二分法
2. 移动、比较、查找：双指针
3. 从前往后不行 试试 从后往前
4. 移动相关：数组反转
5. 自定义排序（<升序 、 >降序）

要遍历和其他每个元素进行比较：
两数之和：Hash、最长无重复：队列…【因为都含有contains()方法】

需要去重：HashSet和HashMap

---

二、二维数组

数据结构及操作函数（一维[ ]变为[ ][ ]）

声明

var n [][]T
n := make([][]T,0)
n := [][]T{}

特殊算法

DFS求矩阵中相邻1的最大和：

class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        int maxSum = 0;
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                if(grid[i][j] == 1){
                    maxSum = Math.max(maxSum,dfs(grid,i,j));
                }
            }
        }
        return maxSum;
    }
    
    //递归 推荐
    public static int dfs(int[][] grid,int i,int j){
        if(i < 0 || j< 0 || i>=grid.length || j>=grid[0].length || grid[i][j] == 0){
            return 0;
        }
        grid[i][j] = 0;
        return 1+dfs(grid,i+1,j)+dfs(grid,i,j+1)+dfs(grid,i-1,j)+dfs(grid,i,j-1);
    }
    
    // 栈
    public static int sumIndex(int[][] grid,int x,int y){
        if(grid[x][y] == 0) return 0;
        Deque<Integer> stacki = new ArrayDeque<>();
        Deque<Integer> stackj = new ArrayDeque<>();
        stacki.push(x);
        stackj.push(y);
        grid[x][y] = 0;
        int ans = 0;
        while(!stacki.isEmpty()){
            int i = stacki.pop();
            int j = stackj.pop();
            ans++;
            if(i+1 < grid.length && grid[i+1][j] == 1){
                stacki.push(i+1);
                stackj.push(j);
                grid[i+1][j] = 0;
            }
            if(j+1 < grid[0].length && grid[i][j+1] == 1){
                stacki.push(i);
                stackj.push(j+1);
                grid[i][j+1] = 0;
            }
            if(i-1 > -1 && grid[i-1][j] == 1){
                stacki.push(i-1);
                stackj.push(j);
                grid[i-1][j] = 0;
            }
            if(j-1 > -1 && grid[i][j-1] == 1){
                stacki.push(i);
                stackj.push(j-1);
                grid[i][j-1] = 0;
            }
        }
        return ans;
    }
}

三、链表

数据结构及操作函数

算法常常以这种方式出链表：

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */

Go中的链表list：和sync.Map{}一样支持所有数据类型

	l := &list.List{}
	l.Len()
	f := l.Front()
	b := l.Back()

for i := ll.Front(); i != nil; i = i.Next() {
		fmt.Println(i.Value)
	}

思路

1. 在原链表上准备操作就在头节点前添加一个哨兵节点，不然头结点情况要特殊处理！！！
2. 查找：双指针
3. 最复杂也就是：哨兵+双指针
4. 链表合并：给任意一个加一个哨兵节点【注意：哨兵节点要保留住 要以ans.next返回呢】
5. 链表排序使用归并！！！

特殊算法：

1. 快慢指针注意点
   - 使用fast.Next
   - fast先传递

	for fast.Next != nil {
	     fast = fast.Next.Next
	     if fast == nil {
	         break
	     }
	     slow = slow.Next
	 }

2. 算法实现LRU：map + 双向链表

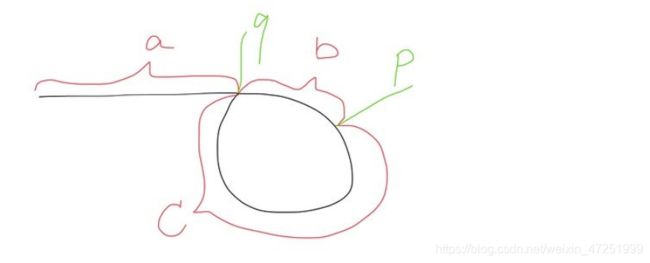
3. 入环点： 其实是道数学问题：2(a+b) = a+b+n(c+b) ==> a=(n-1)(c+b)+c（快指针已经走了n圈）
   

4. 两链相交点： 也是一道数学问题 我走了你走过的路，你走了我走过的路，然后我们就相遇了 （不相遇的时候最终也会想等 只不过相等值为nil）

---

四、字符串

数据结构及操作函数

基本操作

	s := "abcd123你哈"
	len(s) // 字节数
	for i := 0; i < len(s); i++ {
		fmt.Println(s[i]) //字节
	}
	for index, c := range s {
		fmt.Println(index,c) //字符
	}
	
	b := []byte(s) //转换为字节切片
	r := []rune(s) //转换为字符切片

strings包：https://studygolang.com/static/pkgdoc/pkg/strings.htm

strconv包：

	// string ===> int
	atoi, err := strconv.Atoi(s)
	// int ===> string
	itoa := strconv.Itoa(123)

---

五、动态规划 (求最优解)

三步走

• 列出子状态
• 列出父子状态转移方程
• 初始化状态定义数组

思路

一维数组： int dp = array[0];
二维数组： int[] pd = new int[array[0].length+1];
① 只能向右或向下
② 左上角到右下角路径问题

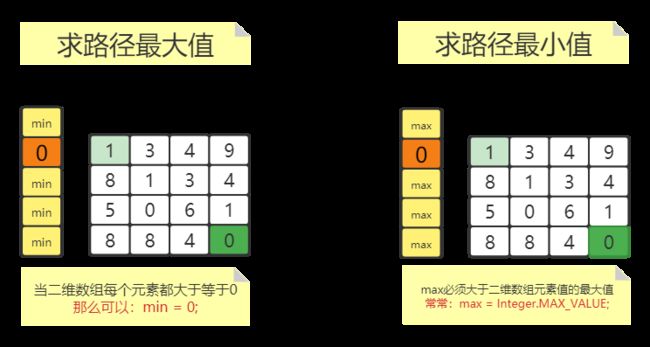
还有一种方法就是不创建新数组，直接修改二维数组中的值。
思路： 先计算出第一行与第一列，然后从（1，1）点开始 Math.min/max......

---

六、回溯算法（求所有可能）

注意⚠️： 返回所有可能的确切值：回溯算法；返回所有可能的数量：动态规划！

三步走

• 判断此选择是否满足条件
• 遍历所有下一步选择
• 选择 - 递归 - 删除选择

---

七、贪心算法（每步都是最优解）

---

八、二叉树（常用递归）

1. Z字形遍历，依旧队列按层遍历 list.add(0,node.val);//每次加到0的位置，就自动逆序了
2. 递归遍历其实就是一种深度遍历思想！（因为递归和栈可以互替）
   DFS（递归 / 栈） 【递归考虑两点：1.root和左右子节点的关系！2.叶子节点时返回结果！】
   BFS（队）
3. 注意叶子结点的终止条件
4. 任意节点间路径问题：
   路径：在二叉树中走一条线 且每个节点只走一遍
   124. 二叉树中最大路径和
   543. 二叉树的直径

func diameterOfBinaryTree(root *TreeNode) int {
    // 全局遍历作为最终结果
    var res int
    // 求数深度函数
    var depth func(*TreeNode) int
    depth = func(node *TreeNode) int {
    	......
    	/ 递归求左右子树的深度
        leftDepth := depth(node.Left)
        rightDepth := depth(node.Right)
        
        ......
        将root + left + right 作为更新最终结果res的一种情况
		......
        / 而只将 root+left 和 root+right作为返回的结果
        return max(leftPath,rightPath)+1
    }
    depth(root)
    return res
}

---

九、分治算法

分治算法能解决的问题，一般需要满足下面这几个条件：

1. 原问题与分解成的小问题具有相同的模式；
2. 原问题分解成的子问题可以独立求解，子问题之间没有相关性；
3. 具有分解终止条件，也就是说，当问题足够小时，可以直接求解；
4. 可以将子问题合并成原问题，而这个合并操作的复杂度不能太高，否则就起不到减小算法总体复杂度的效果了。

回想归并排序的merge函数就可以

实现

分治算法一般都比较适合用递归来实现：

1. 分解：将原问题分解成一系列子问题；（递的过程）
2. 解决：递归地求解各个子问题，若子问题足够小，则直接求解；（终止条件）
3. 合并：将子问题的结果合并成原问题。（归的过程）

代码顺序：终止条件==>递的过程==>归的过程

十、图

方法

DFS（栈 / 递归）

递归：往往递归简单一点 始终记住：重复递归的假设已经存在，只考虑①第一步和第二步怎么写，以及②递归结束标志！！！

栈：一定在入栈(队)后立即标记

	Deque<Integer> stack = new ArrayDeque<>();
	stack.push(start);
	stack.pop();
	stack.peek();//返回但不弹出

BFS（队）
需要多源广度搜索，只需要把最初出的多个源点一起入队（leecode 994）

	Queue<Integer> queue = new LinkedList<>();
	queue.add(start);
	queue.poll();
	queue.peek();//返回但不弹出

相同与区别：DFS节点周围的都入栈，取栈顶元素；BFS节点周围的都入队，出队头元素。

特殊算法

拓扑排序

当出现点与点有向关联：画图 ⇒ 拓扑排序 【map存节点+入度】

func canFinish(numCourses int, prerequisites [][]int) bool {
    / topo[节点]入度
    topo := make(map[int]int,numCourses)
    。。。
    / 入度为0的节点存入stack
    stack := []int{}
    for i:=0;i<numCourses;i++ {
        if topo[i] == 0 {
            stack = append(stack,i)
        }
    }
    count := 0 / 也可以是[]res 返回拓扑过程
    for len(stack) > 0 {
        // 取出入度为0的节点
        zeroIndegree := stack[len(stack)-1]
        stack = stack[:len(stack)-1]
        count++
        // 将0度节点所指向的节点的入度减1
        for _,v := range prerequisites {
            if v[1] == zeroIndegree {
                topo[v[0]]--
                / 注意 ：直接在这里再获取入度为0的点
                if topo[v[0]] == 0 {
                    stack = append(stack,v[0])
                }
            }
        }
    }
    return count == numCourses
}

---

---

常用数据结构与工具包

1. map的声明：map[keyType]valueType)

普通声明

var 变量名 map[keyType]valueType（不会分配数据内存，是nil）

初始化声明

1. 变量名 接受 map[keyType]valueType{k1:v1,k2:v2}
2. 变量名 接受 make(map[keyType]valueType)

添加与获取元素

不存在会返回默认值：

	m := make(map[string]int)

	m["id"] = 2001
	fmt.Println(m["id"])  /2001
	fmt.Println(m["name"])  /0

但其实获取元素时会将是否存在作为第二个元素返回：

	v,ok := m["name"]
	if ok {
		fmt.Println(v)
	}else {
		fmt.Println("不存在")
	}

删除元素

delete(map，键)

遍历map

因为map是没有下标的，所以只能是 forr:（当然，散列表坑定是无序输出）

	mm := map[string]int{"id":1,"name":2001,"age":520}
	
	for k, v := range mm {
		fmt.Println(k,v)
	}

2. math包

import "math"

绝对值：func Abs(x float64) float64
次方值：func Pow(x, y float64) float64 取根号2：fmt.Print(math.Pow(16,0.5))
最大值：func Max(x, y float64) float64
最小值：func Min(x, y float64) float64

平方根：math.Sqrt(32)
立方根：math.Cbrt(27)


向下取整：func Floor(x float64) float64
向上取整：func Ceil(x float64) float64

最大整数：MaxInt64
最小整数：MinInt64

3. ACM模式：fmt.Scan(&n) 只能往读入基本数据类型

import "fmt"

	var n int
	var s string
	num, _ := fmt.Scan(&n, &s)
	if num == 0 {
		fmt.Println("没有元素")
	}else {
		fmt.Println("输入元素：",n,s)
	}

杂记

1. 数据交换：m,n = n,m
2. 注意⚠️： 返回所有可能的确切值：回溯算法；返回所有可能的数量：动态规划！
3. Go支持位运算：mid := (right + left) >> 1
4. 换行声明时会出现,

	tt := &t{
		a:2,
		b:3,
	}

	res := []int{
		3,
	}

5. 10e3 ：10*10³
6. 2³¹：1<<31
7. 奇数：n&1 == 1 ；偶数：n&1 == 0