(转)凸函数
基本介绍
凸函数是一个定义在某个向量空间的凸子集C(区间)上的实值函数f,而且对于凸子集C中任意两个向量
x 1 , x 2 , f ( ( x 1 + x 2 ) / 2 ) ≤ ( f ( x 1 ) + f ( x 2 ) ) 2 x1,x2,f((x1+x2)/2)≤ \frac{(f(x1)+f(x2))}{2} x1,x2,f((x1+x2)/2)≤2(f(x1)+f(x2))
于是容易得出对于任意(0,1)中有理数p,f(px1+(1-p)x2)≤pf(x1)+(1-p)f(x2)。如果f连续,那么p可以改成任意(0,1)中实数。
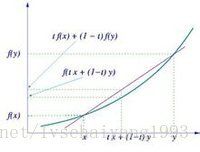
若这里凸集C即某个区间I,那么就是:设f为定义在区间I上的函数,若对I上的任意两点X1,X2和任意的实数λ∈(0,1),总有
f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2),
则f称为I上的凸函数。
判定方法可利用定义法、已知结论法以及函数的二阶导数
对于实数集上的凸函数,一般的判别方法是求它的二阶导数,如果其二阶导数在区间上非负,就称为凸函数。(向下凸)
如果其二阶导数在区间上恒大于0,就称为严格凸函数。
函数性质
性质
定义在某个开区间C内的凸函数f在C内连续,且在除可数个点之外的所有点可微。如果C是闭区间,那么f有可能在C的端点不连续。
一元可微函数在某个区间上是凸的,当且仅当它的导数在该区间上单调不减。
一元连续可微函数在区间上是凸的,当且仅当函数位于所有它的切线的上方:对于区间内的所有x和y,都有f(y) ≥ f(x) + f '(x) (y − x)。特别地,如果f '© = 0,那么c是f(x)的最小值。
一元二阶可微的函数在区间上是凸的,当且仅当它的二阶导数是非负的;这可以用来判断某个函数是不是凸函数。如果它的二阶导数是正数,那么函数就是严格凸的,但反过来不成立。例如,f(x) = x4的二阶导数是f "(x) = 12 x2,当x = 0时为零,但x4是严格凸的。
更一般地,多元二次可微的连续函数在凸集上是凸的,当且仅当它的黑塞矩阵在凸集的内部是正定的。
凸函数的任何极小值也是最小值。严格凸函数最多有一个最小值。
对于凸函数f,水平子集{x | f(x) < a}和{x | f(x) ≤ a}(a ∈ R)是凸集。然而,水平子集是凸集的函数不一定是凸函数;这样的函数称为拟凸函数。
延森不等式对于每一个凸函数f都成立。如果X是一个随机变量,在f的定义域内取值,那么(在这里,E表示数学期望。)
折叠定义及相互关系
定义1 设f(x)在区间I上有定义,f(x)在区间I称为是凸函数当且仅当:∀x1,∀x2∈I,有f[λx1+(1-λ)x2]≤λf(x1)+(1-λ)f(x2)上式中“≤”改成“<”则是严格凸函数的定义.
定义2 设f(x)在区间I上有定义,f(x)在区间I称为是凸函数当且仅当:∀x1,∀x2∈I, 有f[(x1+x2)/2]≤f(x1)/2+f(x2)/2
定义3 设f(x)在区间I上有定义,f(x)在区间I称为是凸函数当且仅当∀x1、x2…xn∈I:有f[(x1+x2+…xn)/n]≤[f(x1)+f(x2)+…f(xn)]/n
定义4 f(x)在区间I上有定义,当且仅当曲线y=f(x)的切线恒保持在曲线以下,则成f(x)为凸函数.若除切点之外,切线严格保持在曲线下方,则称曲线f(x)为严格凸的
引理1 定义2与定义3等价
引理2 若连续,则定义1,2,3等价
相关示例
函数f(x) = x²;处处有,因此f是一个(严格的)凸函数。
绝对值函数f(x) = | x | 是凸函数,虽然它在点x = 0没有导数。
当1 ≤ p时,函数f(x) = | x | p是凸函数。
定义域为[0,1]的函数f,定义为f(0)=f(1)=1,当0函数x3的二阶导数为6x,因此它在x ≥ 0的集合上是凸函数,在x ≤ 0的集合上是凹函数。
每一个在内取值的线性变换都是凸函数,但不是严格凸函数,因为如果f是线性函数,那么f(a + b) = f(a) + f(b)。如果我们把“凸”换为“凹”,那么该命题也成立。
每一个在内取值的仿射变换,也就是说,每一个形如f(x) = aTx + b的函数,既是凸函数又是凹函数。
每一个范数都是凸函数,这是由于三角不等式。
如果f是凸函数,那么当t > 0时,g(x,t) = tf(x / t)是凸函数。
单调递增但非凸的函数包括和g(x) = log(x)。
非单调递增的凸函数包括h(x) = x2和k(x) = − x。
函数f(x) = 1/x2,f(0)=+∞,在区间(0,+∞)内是凸函数,在区间(-∞,0)内也是凸函数,但是在区间(-∞,+∞)内不是凸函数,这是由于x = 0处的奇点。
注:某些教材的凸函数定义与此定义相反,即凸函数与凹函数相反