python实现客户成套订单配送策略混合遗传算法编码
以如下的论文文献为学习对象:2008年发表在《控制工程》的文献《客户成套订单配送策略混合遗传算法研究》
文献研究的学术意义
本文研究的目的是寻求在车队车辆数有限情况下 ,如何合理安排每天的车辆 ,使得总成本最小的方案。另外,若某天车辆不够,在应该租用多少车辆或考虑购置部分车辆来满足未来需求等策略下 ,组合各种策略使得未来一段时间内总成本最小。 目前对这类实际配送问题的研究文献尚不 多,大多数文献只是关于经典的车辆路径问题,因此,研究这类问题有很重要的实际意义。
问题描述
成套订单的配送问题与 VRPTW问题差别只在于将原来的客户需求拆成多点客户需求 ,但 已经不能简单地套用 VRPTW了, 因为在配送过程中可能存在着多辆车经过一个城市的情况 。有人认为将各个卸货点的货物需求集中起来运输就是 VRPTW 了,但若卸货点货物集中起来 的数量超过车辆容量 q,或货物因某些特性不能 放 在 一 起 运 输 ,就不满足VRPTW问题 的条件。纵使不超过 q,但它减少了车辆组合的多样性 。其组合也不一定就是最优。
目标函数
VRPTW问题的目标函数:总运输成本最小;
文献列出数学模型表示的目标函数为双目标函数:使用车辆数量最少以及车辆的总行驶距离最小。由于出动一辆车的固定成本远远大于车辆 的行驶成本 ,所以 ,本文将车辆数最小作为最小总成本的主要 目标 ,而将路程最小作为次要 目标 。
转化成一般的VRPTW问题的策略
本文采取一种增加虚拟卸货节点的方法将成套订 配送问题转化成 VRPTW模型。具体方法很简单,将原来各成套订单的任务按每天的子任务收集在 一起 ,并按卸货点位置合并,合并后每个卸货点有 几个 任务 就将其拆成几个虚拟卸货点 ,拆分前的卸货点与拆分后 的虚拟点两两间距离为 0,而与其他节点的距离不变,这样就可以将成套 订单的配送问题简化为VRPTW 问题 了 。设仓库的编号为 0,客户编号按照增加 了虚拟卸货点之后的卸货点数量来设置 ,即有多少个子任务就有多少个卸货点编号 。
遗传模拟退火算法
详细的步骤请读者参阅文献获取。
模拟退火算法基本原理
模拟退火算法(simulated annealing, SA)算法的思想最早是由Metropolis等提出的。其出发点是基于物理中固体物质的退火与一般的组合优化问题之间的相似性。模拟退火算法是一种通用的优化算法,其物理退火过程由以下三部分组成:
(1)加温过程。其目的是增强粒子的热运行,使其偏离平衡位置。当温度足够高时,固体将熔为液体,从而消除系统原先存在的非均匀状态。
(2)等温过程。对于与周围环境交换热量而温度不变的封闭系统,系统状态的自发变化总是朝自由能减少的进行的,当自由能达到最小时,系统达到平衡状态。
(3)冷却过程。使粒子热运动减弱,系统能量下降,得到晶体结构。
其中,加温过程对应算法的设定初温,等温过程对应算法的Metropolis抽样过程,冷却过程对应控制参数的下降。这里能量的变化就是目标函数,要得到的最优解就是能量最低态。Metropolis准则是SA算法收敛于全局最优解的关键所在,Metropolis准则以一定的概率接受恶化解,这样就使算法跳离局部最优的陷阱。
算例数据
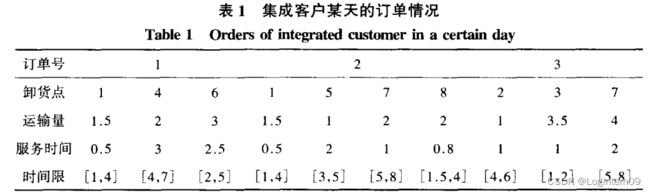
使用遗传模拟退火算法求解如下10个卸货点的VRPTW问题。为了使研究的问题更加有意义,本人将时间限理解为服务点一天的具体可以允许配送的时间。 如果不要求车辆从配送中心出发的时间是统一的并且为0时刻,那么就默认第一个配送节点是一定能赶到的。采取从配送中心出发的时间不为0时刻的策略,默认一定能达到第一个配送点,所以采用最早到达时间推算车辆出发的时间。
假设配送中心营业时间是早上七点至晚上七点。卸货点1-10的时间限制理解如下:卸货点1要求在下午1点至下午4点配送,卸货点1要求的服务时间是半个小时;卸货点2要求在下午4点至下午6点配送,卸货点2要求的服务时间是1个小时,以此类推其他的卸货点的配送及服务时间限制。算法中用到配送及服务时间是下午的情况,例如卸货点1可转成数字表示是[13,16]。
先排除算例无解的场景,即配送中心开门时间都不能实现派车辆运输的场景。取10个卸货点中配送中心距离服务点最大的直线距离长度200公里,再假设车辆的单位行驶速度为40公里/小时,选择服务时间要求最早的1点,计算得出5个小时就可以满足配送任务,那么车辆可以最晚在早上8点前达到;
提前处理算例数据
考虑从配送中心不是0点出发的话,原来文献中的配送时间窗不是很合理,因为都是下午送货比较紧凑很可能没有较多可行解的产生,更改时间窗及服务时间如下数据,其中配送点为0的表示配送中心的服务时间也就是开门关门时间限制:
染色体编码方式
按照客户点的序号(卸货点)设计染色体,一条染色体表示所有卸货点序号的一个排列,车辆路径为从第一个基因往后搜索满足车辆容量和时间窗约束条件的基因,直到不能满足条件为止,满足条件的基因成为一条路线。依次执行此操作,直到最后一个基因。编码方式采用整数编码。
产生初始种群
def set_codeForm(population_size):
population = np.zeros((population_size, demand_node_num), dtype=int)
for i in range(population_size):
while 1:
population[i, :] = random.sample(range(1, demand_node_num+1), demand_node_num)
if get_feasible_route(population[i, :]):
break
else:
continue
return population
计算初始种群中每条染色体的适应度函数
# 目标函数:使用车辆数量最少+车辆的总行驶距离最小。
# 约束条件:车辆载重量限制+硬时间窗限制
# 由于出动一辆车的固定成本远远大于车辆的行驶成本,
# 所以,本文将车辆数最小作为最小总成本的主要目标 ,而将路程最小作为次要目标 。
def main_target_func(chrom):
# 使用车辆数量最少
vehice_num = 0
routes = get_feasible_route(chrom)
for path in routes:
for node in path[1:-1]:
if node == 0:
vehice_num += 1
return vehice_num
def minor_target_func(chrom):
# 车辆的总行驶距离最小
# 适应度函数是总路线长度最小
routes = get_feasible_route(chrom)
total_length = 0
for route in routes:
total_length += get_route_length(route)
target_value = total_length
return target_value
def calculate_fitness(chrom):
target_value = 0.6*main_target_func(chrom) + 0.4*minor_target_func(chrom)
return target_value
按照模拟退火准则生成新种群
每个染色体的领域:邻域结构与中止条件 每个染色体的邻域包括随机使用 2-opt交换和 3-opt交换所产生的所有染色体.中止条件为运行 500代.
参考学习链接如下:
https://baike.baidu.com/item/2-opt
https://blog.csdn.net/sinat_41348401/article/details/126920506
使用matlab实现的3-opt算法
遗传算法的选择策略:轮盘赌选择法
将值最大的染色体直接复制一个进入下一代
Python实现轮盘赌算法
遗传算法的交叉和变异操作
局部收敛进行模拟退火算法的升温操作,否则进行遗传算法的交叉和变异操作。
小结
关联本博主的其他文章:
《遗传算法求解带时间窗的VRP问题(python)》
《【纠错】遗传算法求解VRP计算车辆容量限制的代码有bug》
《如何写代码实现VRP问题中车辆容量限制及时间窗要求(python)》
上面两篇文章都采用遗传算法求解,算得目标函数值478,本博文采用遗传模拟退火算法改进源代码,看看寻优结果。但是没搞出来,文献算法描述细节部分没理解清楚。