分类模型-评估指标(2):ROC曲线、 AUC值(ROC曲线下的面积)【只能用于二分类模型的评价】【不受类别数量不平衡的影响;不受阈值取值的影响】【AUC的计算方式:统计所有正负样本对中的正序对】
评价二值分类器的指标很多,比如precision、recall、F1 score、P-R曲线等。但这些指标或多或少只能反映模型在某一方面的性能。相比而言,ROC曲线则有很多优点,经常作为评估二值分类器最重要的指标之一。
ROC曲线、 AUC值:解决样本不均衡时评价指标的问题。
- 灵敏度(Sensitivity):实际为正样本预测成正样本的概率
S e n s i t i v i t y = T P T P + F N Sensitivity=\cfrac{TP}{TP+FN} Sensitivity=TP+FNTP - 特异度(Specificity):即实际为负样本预测成负样本的概率
R e c a l l = T N F P + T N Recall=\cfrac{TN}{FP+TN} Recall=FP+TNTN - 真正例率(TPR) = 灵敏度 :实际为正样本预测成正样本的概率
T P R = T P T P + F N TPR=\cfrac{TP}{TP+FN} TPR=TP+FNTP - 假正例率(FPR) = 1- 特异度:实际为负样本预测成正样本的概率
F P R = F P F P + T N FPR=\cfrac{FP}{FP+TN} FPR=FP+TNFP - 召回率 = 灵敏度 = 查全率 = 真正率 = T P R = T P T P + F N TPR=\cfrac{TP}{TP+FN} TPR=TP+FNTP,都是指:实际正样本中预测为正样本的概率
- 我们可以看出:
- 真正率和假正率这两个指标跟正负样本的比例是无关的
- 所以当样本比例失衡的情况下,准确率不如真正率、假正率这两个指标好用
一、ROC曲线(Receiver Operating Characteristic Curve)
ROC曲线(Receiver Operating Characteristic Curve)中文名为“受试者工作特征曲线”:
- 横坐标:假阳性率(False Positive Rare), F P R = F P F P + T N = F P N FPR=\cfrac{FP}{FP+TN}=\cfrac{FP}{N} FPR=FP+TNFP=NFP
- FP是N个负样本中被分类器预测为正样本的个数
- N是真实的负样本的数量
- 纵坐标:真阳性率(Ture Positive Rare), T P R = T P T P + F N = T P P TPR=\cfrac{TP}{TP+FN}=\cfrac{TP}{P} TPR=TP+FNTP=PTP
- TP是P个正样本中被分类器预测为正样本的个数
- P是真实的正样本的数量
假设有10位疑似癌症患者,其中有3位很不幸确实患了癌症(P=3),另外7位不是癌症患者(N=7)。医院对这10位疑似患者做了诊断,诊断出3位癌症患者,其中有2位确实是真正的患者(TP=2)。那么真阳性率TPR=TP/P=2/3。对于7位非癌症患者来说,有一位很不幸被误诊为癌症患者(FP=1),那么假阳性率FPR=FP/N=1/7。对于“该医院”这个分类器来说,这组分类结果就对应ROC曲线上的一个点(1/7,2/3)。
既然已经这么多评价标准,为什么还要使用ROC和AUC呢?因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。下图是ROC曲线和Precision-Recall曲线的对比:

在上图中,(a)和(c)为ROC曲线,(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果,(c)和(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果。可以明显的看出,ROC曲线基本保持原貌,而Precision-Recall曲线则变化较大。
二、AUC值
AUC(Area Under Curve)被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。
又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。
使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好,而作为一个数值,对应AUC更大的分类器效果更好。AUC越大,说明分类器越可能把真正的正样本排在前面,分类性能越好。
AUC就是:随机抽出一对样本 ( 正样本 i , 负样本 j ) (\text{正样本}_i,\text{负样本}_j) (正样本i,负样本j),然后用训练得到的分类器来对这两个样本进行预测,预测得到正样本的概率 p r e d i pred_i predi 大于负样本概率 p r e d j pred_j predj 的概率。
三、AUC值的意义
知道了如何计算AUC值,我们当然是要来问一下AUC值的意义了。为什么我们要这么大费周章地搞出这个AUC值?
假设我们有一个分类器,输出是样本输入正例的概率,所有的样本都会有一个相应的概率,这样我们可以得到下面这个图:
- 横轴表示预测为正例的概率;
- 纵轴表示样本数;
所以,蓝色区域表示所有负例样本的概率分布,红色样本表示所有正例样本的概率分布。显然,如果我们希望分类效果最好的话,那么红色区域越接近1越好,蓝色区域越接近0越好。
为了验证你的分类器的效果。你需要选择一个阈值,比这个阈值大的预测为正例,比这个阈值小的预测为负例。如下图:

在这个图中,阈值选择了0.5于是左边的样本都被认为是负例,右边的样本都被认为是正例。可以看到,红色区域与蓝色区域是有重叠的,所以当阈值为0.5的时候,我们可以计算出准确率为90%.
好,现在我们来引入ROC曲线。

图中左上角就是ROC曲线,其中横轴就是前面说的FPR(False Positive Rate),纵轴就是TPR(True Positive Rate)。
然后我们选择不同的阈值时,就可以对应坐标系中一个点。

当阈值为0.8时,对应上图箭头所指的点。

当阈值为0.5时,对应上图箭头所指的点。
这样,不同的阈值对应不同的点。最后所有的点就可以连在一起形成一条曲线,就是ROC曲线。
现在我们来看看,如果蓝色区域与红色的区域发生变化,那么ROC曲线会怎么变呢?

上图中,蓝色区域与红色区域的重叠部分不多,所以可以看到ROC曲线距离左上角很近。

但是,当蓝色区域与红色区域基本重叠时,ROC曲线就和接近y=x这条线了。
综上两个图,如果我们想要用ROC来评估分类器的分类质量,我们就可以通过计算AUC(ROC曲线下的面积)来评估了,这就是AUC的目的。
其实,AUC表示的是正例排在负例前面的概率。

比如上图,第一个坐标系的AUC值表示,所有的正例都排在负例的前面。第二个AUC值,表示有百分之八十的正例排在负例的前面。
我们知道阈值可以取不同,也就是说,分类的结果会受到阈值的影响。如果使用AUC的话,因为阈值变动考虑到了,所以评估的效果更好。
另一个好处是,ROC曲线有一个很好的特性:当测试集中的正负样本分布发生变化了,ROC曲线可以保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。
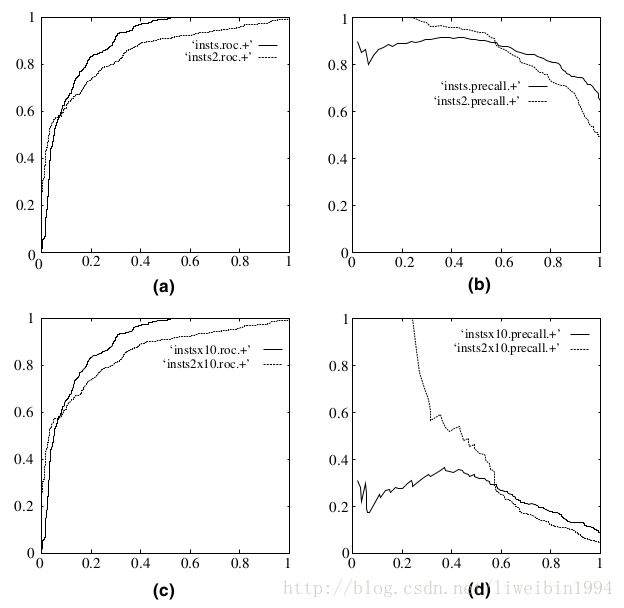
在上图中,(a)和©为ROC曲线,(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果,©和(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果。可以明显的看出,ROC曲线基本保持原貌,而Precision-Recall曲线则变化较大。
四、代码实现AUC
def Cal_AUC(label, pred):
positive = [] # [0, 1, 7]
negetive = [] # [2, 3, 4, 5, 6]
auc_value = 0
for index, l in enumerate(label):
if l == 0:
negetive.append(index)
else:
positive.append(index)
M = len(positive)
N = len(negetive)
# 遍历所有正负样本对【正负样本对的数量 = M*N】
for i in positive:
for j in negetive:
# (0.9, 0.3)、(0.9, 0.1)、(0.9, 0.4)、(0.9, 0.9)、(0.9, 0.66)---->4.5
# (0.8, 0.3)、(0.8, 0.1)、(0.8, 0.4)、(0.8, 0.9)、(0.8, 0.66)---->4
# (0.7, 0.3)、(0.7, 0.1)、(0.7, 0.4)、(0.7, 0.9)、(0.7, 0.66)---->4
pred_i, pred_j = pred[i], pred[j]
if pred_i > pred_j:
auc_value += 1
elif pred_i == pred_j:
auc_value += 0.5
auc = auc_value * 1.0 / (M * N) # 12.5/15=0.8333333333333334
return auc
label = [1, 1, 0, 0, 0, 0, 0, 1]
pred = [0.9, 0.8, 0.3, 0.1, 0.4, 0.9, 0.66, 0.7]
print("my_auc:", Cal_AUC(label, pred))
from sklearn import metrics
auc = metrics.roc_auc_score(label, pred) # 0.8333333333333334
print('sklearn-auc:', auc)
五、ROC曲线相比P-R曲线有什么特点?
在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。
相比P-R曲线,ROC曲线有一个特点,当正负样本的分布发生变化时,ROC曲线的形状能够基本保持不变,而P-R曲线的形状一般会发生较剧烈的变化。
下图是ROC曲线和Precision-Recall曲线的对比:

在上图中,(a)和(c)为ROC曲线,(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果,(c)和(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果。
可以明显的看出,ROC曲线基本保持原貌,而Precision-Recall曲线则变化较大。
这个特点让ROC曲线能够尽量降低不同测试集带来的干扰,更加客观地衡量模型本身的性能。这有什么实际意义呢?在很多实际问题中,正负样本数量往往很不均衡。比如,计算广告领域经常涉及转化率模型,正样本的数量往往是负样本数量的1/1000甚至1/10000。若选择不同的测试集,P-R曲线的变化就会非常大,而ROC曲线则能够更加稳定地反映模型本身的好坏。所以,ROC曲线的适用场景更多,被广泛用于排序、推荐、广告等领域。
但需要注意的是,选择P-R曲线还是ROC曲线是因实际问题而异的,如果研究者希望更多地看到模型在特定数据集上的表现,P-R曲线则能够更直观地反映其性能。
参考资料:
一文彻底搞懂AUC
Understanding AUC - ROC Curve
【小萌五分钟】机器学习 | 模型评估: ROC曲线与AUC值
Lesson 5.ROC-AUC指标详解|机器学习评估指标
单标签分类评价指标(精确率,召回率,F1,AUC值计算,ROC曲线,混淆矩阵)
【机器学习】手撕AUC的计算
AUC详解与python实现

