机器学习（二）——贝叶斯分类器

1. 贝叶斯决策论

核心： 将最小化分类错误率转换为最大化先验概率和类条件概率（似然）的乘积。

1.1 贝叶斯判定准则

（1）期望损失$R(c_i|x)$
假设有N种可能的类别标记，即$\gamma =\{c_1,c_2,\cdots ,c_N\}$。${\lambda }_{ij}$是将真实标记为$c_j$的样本误分类为$c_i$所产生的损失。基于后验概率$P(c_i|x)$可获得将样本x分类为$c_i$所产生的期望损失：
$$R(c_i|x)=\sum _{j=1}^N{\lambda }_{ij}P(c_j|x)$$

（2）最小条件风险的类别标记$h^{\ast }(x)$
根据贝叶斯判定准则：为最小化总体风险，需要每个样本选择使条件风险最小的类别标记。
$$h^{\ast }(x)=\arg \underset{c\in \gamma }{\min }R(c|x)$$

（3）最小化分类错误率的贝叶斯最优分类器

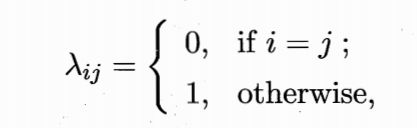
此时条件风险以及最优分类器为：
$$\begin{gathered} R(c|x)=1-P(c|x) \\ {h}^{\ast }(x)=\arg \underset{c\in \gamma }{\max }P(c|x) \end{gathered}$$

因此问题转换为了基于有限的训练样本集尽可能准确地估计后验概率$P(c|x)$。求最小化条件风险即最大化后验概率。
因此可以采用生成式模型，考虑到贝叶斯定理：
$$p(c|x)=\frac{p(x|c)p(c)}{p(x)}$$

其中，$P(c)$是类先验概率；$P(x|c)$是样本相对于类标记c的类条件概率，也称似然（likelihood）。最大化后验概率即最大化先验概率和似然的乘积。

理解：
①利用$\lambda$取值，将条件风险转化为了后验概率$P(c|x)$。
②基于贝叶斯准则，我们将后验概率转化为了如何利用训练数据集估计先验概率$P(c)$和似然$P(x|c)$。
（条件风险 --> 后验概率 --> 先验概率和似然）

• 根据大数定律，当训练集样本包含充足的独立同分布样本时，$P(c)$可通过各类样本出现的概率进行估计。
• 直接使用概率估计$P(x|c)$是不行的，因为现实应用中，很多样本取值在训练集中根本没有出现。因此“未被观察到”不能等效为“出现概率为0”.

1.2 极大似然估计

（1）常用策略
假设$P(x|c)$具有确定的形式并且被参数向量${\theta }_c$唯一确定，我们将$P(x|c)$标记位$P(x|{\theta }_c)$。

极大似然估计（MLE）采用频率主义学派的方法，通过优化似然函数确定参数值。

（2）公式

为了防止连乘操作造成下溢，使用对数似然（log-likelihood）
$$LL({\theta }_c)=\sum _{x\in D_c}\log P(x|{\theta }_c)$$

此时参数${\theta }_c$的极大似然估计为：
$$\widehat{{\theta }_c}=\arg \underset{{\theta }_c}{\max }LL({\theta }_c)$$

（3）优缺点

• 通过参数化的方法使类条件概率估计变得简单
• 准确度严重依赖于假设分布形式是否符合潜在的真实数据分布。

2. 朴素贝叶斯分类器

• 基于1.1的贝叶斯准则，将条件风险转化为了先验概率和似然。
• 又基于1.2极大似然估计获得了通过优化似然函数得到极大似然估计的方法。
• 采用“属性条件独立性假设”：假设每个属性独立地对分类结果发生影响。

（1）贝叶斯分类器
基于属性条件独立性假设和贝叶斯准则，可得：
$$P(c|x)=\frac{P(c)P(x|c)}{P(x)}=\frac{P(c)}{P(x)}\prod _{i=1}^{d}P(x_i|c)$$

为了获得最大化后验概率，根据极大似然估计可得：
$$h_{nb}(x)=\arg \underset{c\in \gamma }{\max }P(c)\prod _{i=1}^{d}P(x_i|c)$$

其中${\prod }_{i=1}^{d}P(x_i|c)$可以通过训练集样本分布获得，先验概率$P(c)$：

• 离散属性：
  
• 连续属性：
  

2.1 拉普拉斯平滑

目的
为了避免其他属性携带的信息被训练集中未出现的属性抹去，在估计概率是通常进行平滑。

举例： 假设可以通过8个属性判断西瓜好坏。假设对于一个样本，其中7个属性都指向该西瓜为好瓜。但最后一个属性不在训练集中出现，统计概率为0.这很可能不符合实际预期。

公式：
令N表示训练集可能类别数（标签数），$N_i$表示第i个属性可能的取指数，则拉普拉斯修正为：
$$\begin{gathered} \hat{P}(c)=\frac{|D_c|+1}{|D|+N} \\ \hat{P}(x_i|c)=\frac{|D_{c,x_i}+1|}{|D_c|+N_i} \end{gathered}$$

2.2 示例

Step1：训练样本
Step2：计算$P(x_i|c)$的概率（未发生平滑）
Step2：考虑拉普拉斯修正后，计算$P(x_i|c)$的概率

Step3：利用极大似然估计求解，并获得属性划分
由于P(好瓜)>P(坏瓜)，因此将样本判定为好瓜。