数据结构之队列【超详解】

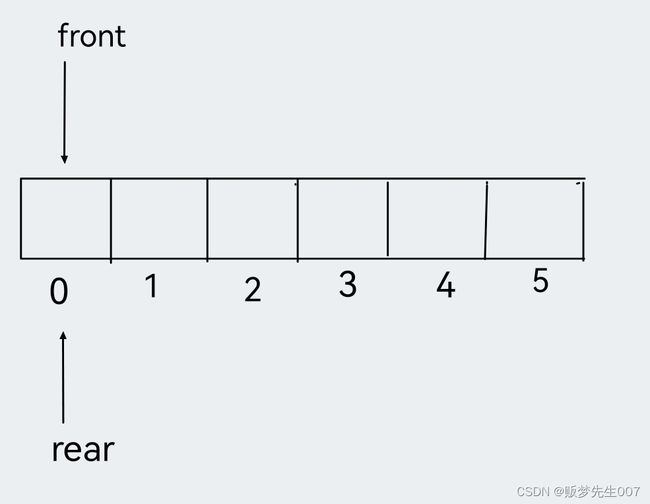
顺序队列的定义

和栈相反，队列是一种先进先出的线性表，它只允许在表的一端进行插入，二在另一端删除元素，允许插入的一端叫队尾，删除元素的一端叫对头

typedef int status;
typedef int qeelemtype;

typedef struct {
	qeelemtype data[MAXSIZE];
	int front;//队头指针
	int rear;//队尾指针
}squeue;

队列初始化

//队列初始化
status initsqueue(squeue *sq){
	sq->front = sq->rear = 0;
	return OK;
} 

队列是否为空

//队列是否为空
status emptysq(squeue *q){
	if(q->front == q->rear)
	return OK;
	else return FALSE;
} 

队尾插入

//队尾插入
status insqueue(squeue *q,qeelemtype e){
	if((q->rear+1)%MAXSIZE ==q->front)
	return ERROR;
	
	q->data[q->rear] = e;
	q->rear = (q->rear+1)%MAXSIZE;
	return OK;
} 

返回队头

//返回对头
status gethead(squeue *q,qeelemtype *e){
	if(q->front == q->rear)
	return ERROR;
	*e = q->data[q->front];
	return OK;
} 

队头删除

//出队 
status dqueue(squeue *q,qeelemtype *e) {
	if(q->front == q->rear)
	return ERROR;
	*e = q->data[q->front];
	q->front = (q->front+1)%MAXSIZE;
	return OK;
} 

双端队列

双端队列是限定插入和删除操作在表的两端进行的线性表，但实际的应用却很少

链队列

单链队列初始化

typedef int Status;
typedef int qeelemtype;

typedef struct QNode
{
	qeelemtype data;
	struct QNode* next;
}QNode,*Queueptr;
typedef struct
{
	Queueptr front;//队头指针
	Queueptr rear;//队尾指针
}LinkQueue;

队列初始化

//队列初始化
Status InitQueue(LinkQueue& Q)
{
	Q.front = Q.rear = (Queueptr)malloc(sizeof(QNode));
	if (!Q.front)exit(-1);
	Q.front->next = NULL;
	return OK;
}

销毁队列

//销毁队列
Status DestroyQueue(LinkQueue& Q)
{
	while (Q.front)
	{
		Q.rear = Q.front->next;
		free(Q.front);
		Q.front = Q.rear;
	}
	return OK;
}

队尾插入

//队尾插入
Status EnQueue(LinkQueue& Q, qeelemtype e)
{
	Queueptr p = (Queueptr)malloc(sizeof(QNode));
	if (!p)exit(-1);
	p->data = e;
	p->next = NULL;
	Q.rear->next = p;
	Q.rear = p;
	return OK;
}

队头删除

//队头删除
Status DeQueue(LinkQueue& Q, qeelemtype& e)
{
	if (Q.front == Q.rear)return ERROR;
	Queueptr p = Q.front->next;
	e = p->data;
	Q.front->next = p->next;
	if (Q.rear == p) Q.rear = Q.front;
	free(p);
	return OK;
}

队列的遍历

//输入元素↓
int PrintQueue(LinkQueue& Q)
{
	QueuePtr p;
	printf("链式队列中的元素");
	if (Q.front->next != NULL)
	{
		p = Q.front->next;
		do
		{
			printf("%5d", p->data);
			p = p->next;
		} while (p != NULL);
	}
	else
		printf("队列为空\n");
	printf("\n");
	return 0;
}//遍历链式队列

测试

void main()
{
	int n, e, i;
	LinkQueue Q;
	InitQueue(Q);
	printf("\n"); printf("\n");
	printf("初始化队列成功！");
	printf("\n"); printf("\n");

	printf("请输入要进队的元素个数：\n");
	scanf("%d", &n);
	for (i = 1; i <= n; i++)
	{
		printf("请输入要进队的元素：\n");
		scanf("%d", &e);
		if (EnQueue(Q, e))
			printf("元素 %d 进队成功\n", e);
		else
			printf("进队失败\n");
	}
	printf("\n");
	PrintQueue(Q);
	printf("\n"); printf("\n");
	printf("删除元素后的队列：\n");
	printf("\n");
	DeQueue(Q, e);
	PrintQueue(Q);
	printf("\n"); printf("\n");
}

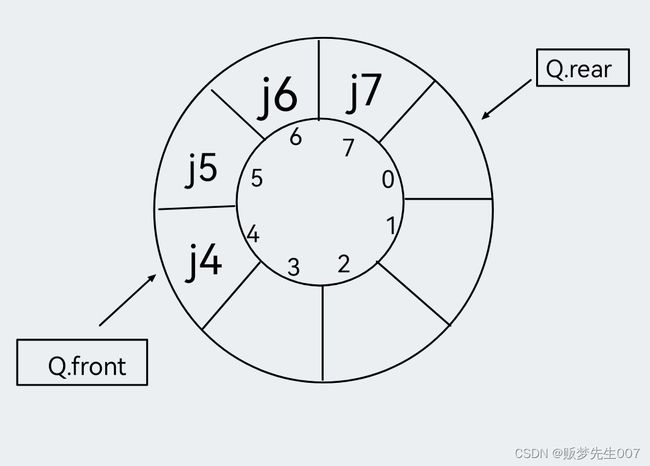
循环队列

当队列处于图d时，不可再继续插入新的队尾元素，否则会因为数组越界导致代码被破坏，如果继续扩大空间的话，就造成了空间的浪费，所以我们将顺序队列假想成如下图一样的环状空间，称之为循环队列

循环队列有头指针和尾指针：
头指针指向对列头部元素，随着对列出队而变化，元素入队时不变化
尾指针指向对列尾部元素，随着对列入队而变化，元素出队时不变化

• 所以我们只需移动指针来控制插入和删除元素
• 遍历的时间复杂度为O（1）
• 插入、删除的时间复杂度为O（1）

此部分代码借鉴李四老师的

初始化循环队列

/*
初始化循环队列
*/
Status InitSeqQueue(SeqQueue* queue)
{
	if (!queue)
	{
		return ERROR;
	}
	queue->front = queue->rear = 0;
	return OK;
}

清空对列

/*
清空队列
*/
Status ClearSeqQueue(SeqQueue* queue)
{
	if (!queue)
	{
		return ERROR;
	}
	queue->front = queue->rear = 0;
	return OK;
}

判断队列是否为空

/*
判断循环队列是否为空
*/
Status EmptySeqQueue(SeqQueue* queue)
{
	if (!queue)
	{
		return ERROR;
	}
	if (queue->front == queue->rear)
	{
		return TRUE;
	}
	return FALSE;
}

循环队列的长度

/*
循环队列的元素个数
*/
int LengthSeqQueue(SeqQueue* queue)
{
	if (!queue)
	{
		return ERROR;
	}
	if (queue->front == queue->rear)
	{
		return 0;
	}
	//留的那个空单元不算做元素个数 
	return (queue->rear - queue->front + QUEUESIZE) % QUEUESIZE;
}

获取队头元素

/*
获取循环队列头元素
*/
Status GetHead(SeqQueue* queue)
{
	if (!queue)
	{
		return ERROR;
	}
	if (queue->front == queue->rear)
	{
		return ERROR;
	}
	return queue->data[queue->front];
}

队尾插入

*
往队尾添加元素
*/
Status AddQueue(SeqQueue* queue, EleType e)
{
	//队满或空指针
	if (!queue)
	{
		return ERROR;
	}
	//刚好队尾再走一个单元就到队头，说明栈满了。
	if ((queue->rear + 1) % QUEUESIZE == queue->front)
	{
		return ERROR;
	}
	queue->data[queue->rear] = e;
	queue->rear = (queue->rear + 1) % QUEUESIZE;//若到队尾转到数组头部
	return OK;
}

队头删除

/*
队头删除元素
*/
Status DelQueue(SeqQueue* queue, EleType* e)
{
	//空指针
	if (!queue)
	{
		return ERROR;
	}
	//队空
	if (queue->front == queue->rear)
	{
		return ERROR;
	}
	*e = queue->data[queue->front];
	queue->front = (queue->front + 1) % QUEUESIZE;//若到队尾转到数组头部
	return OK;
}

队列打印

void PrintfQueue(SeqQueue* queue)
{
	//空指针
	if (!queue)
	{
		return;
	}
	//队空
	if (queue->front == queue->rear)
	{
		return;
	}
	int begin = queue->front;
	while (begin != queue->rear)
	{
		printf("%d,", queue->data[begin]);
		if (begin < QUEUESIZE - 1)
		{
			begin++;
		}
		else
		{
			begin = begin + 1 - QUEUESIZE;
		}

	}
	printf("\n");
	return;
}