C语言 数据结构 二叉树的链式存储 基本操作(附输入样例和讲解)
代码参照了严蔚敏、吴伟民编写的数据结构(C语言版)。
部分内容参考了这位大佬:
https://www.cnblogs.com/cpoint/p/3479788.html
所有代码采用C语言编写。讲解请查看注释。
头文件及宏定义
#includetypedef定义数据类型和结构体
typedef char TElemType;//二叉树结点的值是字符
typedef int Status;
typedef struct BiTNode{
TElemType data;
struct BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;
InitBiTree
Status InitBiTree(BiTree *T){//创建空二叉树
*T=NULL;
return OK;
}
DestoryBiTree
Status DestoryBiTree(BiTree *T){//销毁二叉树
if((*T)->lchild)
DestoryBiTree(&(*T)->lchild);
if((*T)->rchild)
DestoryBiTree(&(*T)->rchild);
free(*T);
*T=NULL;
return OK;
}
CreateBiTree
/*
按照先序顺序输入元素创建二叉树,该创建过程与先序遍历相似
这里有两种写法,写法1:
*/
Status CreateBiTree(BiTree* T){//根据输入数据来创建二叉树
/*
这样写的时候为什么不能用BiTNode* T呢?
因为传入的参数*T是指针,而函数内得所有操作都是对指针进行的,属于对形参进行无效操作。
正确的做法是使用BiTree* T,相当于BiTNode** T,通过 指针的指针 对 指针 进行操作。
*/
char ch;
scanf("%c",&ch);
if(ch==' '){
*T=NULL;
}
else{
*T=(BiTNode*)malloc(sizeof(BiTNode));
(*T)->data=ch;
CreateBiTree(&(*T)->lchild);
CreateBiTree(&(*T)->rchild);
}
}
/*
写法2:
这种写法避免了直接对形参BiTNode* T指针进行操作;
而是通过指针指向某些内容,对节点的数值、左右孩子进行操作。
*/
/*
Status CreateBiTree(BiTNode* T){
char ch;
scanf("%c",&ch);
if(ch==' '){
T->data='\0';
T->lchild=NULL;
T->rchild=NULL;
}
else{
T->data=ch;
BiTNode* l=(BiTNode*)malloc(sizeof(BiTNode));
BiTNode* r=(BiTNode*)malloc(sizeof(BiTNode));
T->lchild=l;
T->rchild=r;
CreateBiTree(l);
CreateBiTree(r);
}
}
*/
BiTreeEmpty
Status BiTreeEmpty(BiTree T){//判断二叉树是否存在,这里只需判断根
if(!T)
return False;
else
return True;
}
BiTreeDepth
int BiTreeDepth(BiTree T){//计算二叉树深度
if(T==NULL){
return 0;
}
else{
int i,j;
i=BiTreeDepth(T->lchild);
j=BiTreeDepth(T->rchild);
if(i>j) return ++i;
else return ++j;
}
}
Root
Status Root(BiTree T){//输出根
printf("%c\n",T->data);
return OK;
}
Value
Status Value(BiTree T,TElemType e){//判断e是否是二叉树中的值
if(T->data==e){
return True;
}
else{
int i=0,j=0;
if(T->lchild){
i=Value(T->lchild,e);
}
if(T->rchild){
j=Value(T->rchild,e);
}
if(i==True||j==True) return True;
else return False;
}
return False;
}
Assign
Status Assign(BiTree *T,TElemType e,TElemType value){//将二叉树中存储的值e改为value
//使用BiTree *T的原因同CreateBiTree(BiTree* T),因为在这个函数中改变了值为e的节点的值。
if((*T)->data==e){
(*T)->data=value;
return True;
}
else{
int i=0,j=0;
if((*T)->lchild){
i=Assign(&(*T)->lchild,e,value);
}
if((*T)->rchild){
j=Assign(&(*T)->rchild,e,value);
}
if(i==True||j==True) return True;
else return False;
}
return False;
}
Parent
Status Parent(BiTree T,TElemType e){//找值为e的节点的双亲节点
if(T->lchild&&T->lchild->data==e){
printf("双亲节点为:%c\n",T->data);
return True;
}
else if(T->rchild&&T->rchild->data==e){
printf("双亲节点为:%c\n",T->data);
return True;
}
else{
if(T->lchild){
Parent(T->lchild,e);
}
if(T->rchild){
Parent(T->rchild,e);
}
}
return False;
}
LeftChild
Status LeftChild(BiTree T,TElemType e){//找值为e的节点的左孩子
if(T->data==e&&T->lchild){
printf("左孩子节点为:%c\n",T->lchild->data);
return True;
}
else{
if(T->lchild){
LeftChild(T->lchild,e);
}
if(T->rchild){
LeftChild(T->rchild,e);
}
}
return False;
}
RightChild
Status RightChild(BiTree T,TElemType e){//找值为e的节点的右孩子
if(T->data==e&&T->rchild){
printf("右孩子节点为:%c\n",T->rchild->data);
return True;
}
else{
if(T->lchild){
RightChild(T->lchild,e);
}
if(T->rchild){
RightChild(T->rchild,e);
}
}
return False;
}
LeftSibling
Status LeftSibling(BiTree T,TElemType e){//找值为e的节点的左兄弟
if(T->lchild&&T->rchild->data==e){
printf("左兄弟节点为:%c\n",T->lchild->data);
return True;
}
else{
if(T->lchild){
LeftSibling(T->lchild,e);
}
if(T->rchild){
LeftSibling(T->rchild,e);
}
}
return False;
}
RightSibling
Status RightSibling(BiTree T,TElemType e){//找值为e的节点的右兄弟
if(T->rchild&&T->lchild->data==e){
printf("左兄弟节点为:%c\n",T->rchild->data);
return True;
}
else{
if(T->lchild){
RightSibling(T->lchild,e);
}
if(T->rchild){
RightSibling(T->rchild,e);
}
}
return False;
}
InsertChild
Status InsertChild(BiTree T,BiTree p,int i,BiTree c){//向二叉树中插入树
/* 初始条件: 二叉树T存在,p指向T中某个结点,LR为0或1,非空二叉树c与T不相交且右子树为空 */
/* 操作结果: 根据i为0或1,插入c为T中p所指结点的左或右子树。p所指结点的原有左或右子树则成为c的右子树 */
if(i==0){//c的右子树为空,使p的左子树成为c的右子树,并使增加了右子树的c成为p的左子树
c->rchild=p->lchild;
p->lchild=c;
}
else{//c的右子树为空,使p的右子树成为c的右子树,并使增加了右子树的c成为p的右子树
c->rchild=p->rchild;
p->rchild=c;
}
return OK;
}
DeleteChild
Status DeleteChild(BiTree T,BiTree p,int i){//在二叉树中删除树
if(i==0){//删除p的左子树
DestoryBiTree(&p->lchild);
}
else{//删除p的右子树
DestoryBiTree(&p->rchild);
}
return OK;
}
PreOrderTraverse
Status PreOrderTraverse(BiTree T){//先序遍历
if(T!=NULL){
printf("%c",T->data);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
}
InOrderTraverse
Status InOrderTraverse(BiTree T){//中序遍历
if(T!=NULL){
InOrderTraverse(T->lchild);
printf("%c",T->data);
InOrderTraverse(T->rchild);
}
}
PostOrderTraverse
Status PostOrderTraverse(BiTree T){//后序遍历
if(T!=NULL){
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
printf("%c",T->data);
}
}
LevelOrderTraverse
实现此函数需要先实现LinkQueue链队列。
/*
Status LevelOrderTraverse(BiTree T){//层次遍历
LinkQueue lq;
QElemType q;//存储出队的元素
EnQueue(&lq,T->data);//根节点入队
while(QueueEmpty(lq)!=0){//队列不空,则出队
DeQueue(&lq,&q);
printf("%c",q);
if(T->lchild) EnQueue(&lq,T->lchild->data);//若有左孩子,则入队
if(T->rchild) EnQueue(&lq,T->rchild->data);//若有右孩子,则入队
}
return OK;
}
*/
输入样例
很多函数被我注释掉了,需要使用的话自行取消注释。
int main(void){
BiTree bt;
InitBiTree(&bt);
CreateBiTree(&bt);
//BiTreeEmpty(bt);
//BiTreeDepth(bt);
//Root(bt);
//Value(bt,'3');
//Assign(&bt,'3','a');
//Parent(bt,'5');
//LeftChild(bt,'1');
//RightChild(bt,'1');
//LeftSibling(bt,'5');
//RightSibling(bt,'5');
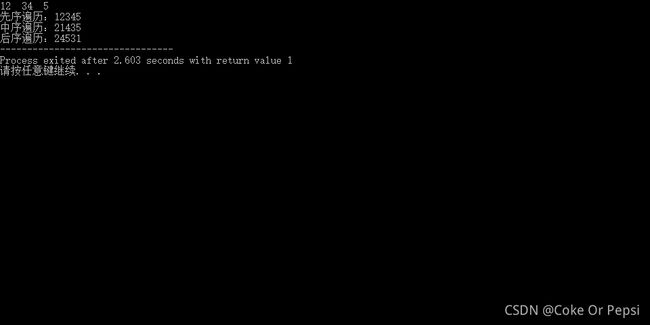
printf("先序遍历:");
PreOrderTraverse(bt);
printf("\n中序遍历:");
InOrderTraverse(bt);
printf("\n后序遍历:");
PostOrderTraverse(bt);
//printf("\n层次遍历:");
//LevelOrderTraverse
DestoryBiTree(&bt);
}