数值分析1-二分法解非线性方程的matlab程序
数值分析1-二分法解非线性方程:
二分法
通过逐次搜索法确定有根区间[a,b],取其中点x0=(a+b)/2将求根区间分成相等的两部分,若中点x0为方程的根,则直接求出方程的根,若x0不是方程的根,则对根进行搜索,判断f(x0)与f(a),f(b)是否同号,若f(x0)与f(a)同号则所求根在x0的右侧,令a1=x0,b1=b,若f(x0)与f(b)同号则所求根在x0的左侧,令a1=a,b1=x0,进行一次迭代后求根区间[a,b]缩小一半变为[a1,b1],对于压缩后的求根区间[a1,b1]进行上述的同样的步骤得到再次的压缩区间[a2,b2],通过循环往复的迭代,有根区间[ak,bk]不断压缩,根的近似值不断提高,达到所要求的精度后停止迭代,得到所想要的根的近似值。
代码:
%二分法求函数的近似实根
clear
clc
format short;
syms x;
f(x)=input('请输入函数表达式,变量用x表示:f(x)=');
a=input('请输入区间左端点:a=');
b=input('请输入区间右端点:b=');
eps=input('请输入停止精度要求:eps='); %% |b-xk|<=eps/2
k=1;
xk=(a+b)/2;
fprintf(' k a f(a) b f(b) xk f(xk)\n');
T=[k,a,f(a),b,f(b),xk,f(xk)]; %T[k,4]=f(b);T[k,6]=f(xk);T初始值为1行7列,随着迭代增加行数
while abs(T(k,4)-T(k,6))>eps/2 %b-xk的绝对值大于误差限,执行循环
k=k+1; %迭代次数加一,迭代次数=K-1;
if k>50
error('迭代出错!或许是迭代初值的问题')
elseif f(xk)*f(a)==0 %
T=[T;k,a,f(a),b,f(b),xk,f(xk)]; %加一行,
break %找到结果,退出循环
elseif f(xk)*f(a)>0 %当f(xk)与f(a)同号
a=xk; %求根区间缩小一半
xk=(a+b)/2; %产生新的区间中点
T=[T;k,a,f(a),b,f(b),xk,f(xk)]; %迭代过程存入T矩阵
elseif f(xk)*f(a)<0 %当f(xk)与f(a)异号号
b=xk; %求根区间缩小一半
xk=(a+b)/2; %产生新的区间中点
T=[T;k,a,f(a),b,f(b),xk,f(xk)]; %迭代过程存入T矩阵
end
end
disp(vpa(T,6));
fprintf('经过%d次迭代,函数方程根的近似解为:x=%.8f\n',k-1,T(k,6))
以对方程f(x)=x^3-x-1二分法求根为例:
①:先通过逐步搜索法确定求根区间[a,b]
②:运行代码块中的二分法代码,命令行依次出现下图状况;
③:按照提示分别输入:函数表达式(按回车结束),求根区间左端点a,求根区间右端点b,求根精度eps;

④:输入参数结束后得到求根结果,如下图:
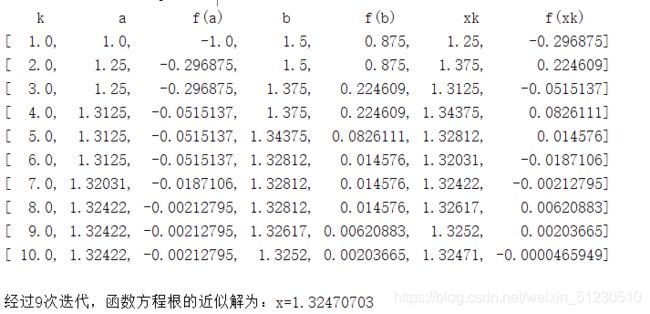
T矩阵中,第七列为f(x)的值,可以看出每次迭代f(x)的值都更加接近与0,根的近似值xk也愈发接近准确解。
xk和f(xk)的值存储在T矩阵的6,7列,可通过输入T(:,6:7),取出矩阵的6至7列,如下图所示:

因为输出数据都是分数,可以通过vpa控制有效数字使之化为小数,输入vpa(T(:,6:7),8),取8位有效数字,结果如下图:

二分法要注意确定求根区间内仅有一个解,当方程有多个解时,不同的求根区间可能对应不同的根,因此求解非线性方程时必须强调自变量x的定义域,即x的求解区间[a,b]; 二分法只要确定了求根区间,那么他一定收敛,只不过可能收敛速度会慢一些。
二分法误差估计:|x*-xk|≤(b-a)/2^(k+1),可通过此式判断所选精度和求根区间对应的迭代次数。
也可以考虑使用内联函数来实现输入所求的非线性方程,但是内联函数inline可能在后续版本更新中被取消,还是使用本文方法为宜。
函数总结:
clc:清屏
clear:清理工作区的数据
format:定义输出数据的格式,short,long等
vpa:控制输出数据的有效数字位数
T(:,3:4):输出T矩阵的3到4列