pytorch实现linear regression

---

前言

本文学习内容来自b站学习视频
Pytorch学这个就够了

---

一、梯度下降是什么？

在机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数，和模型参数值。
梯度下降算法的一个简单的一维函数的理解就是对于以x为函数的损失函数loss(x)，在x=x0处求导，对于求得的这个导数值，若<0,则说明loss(x)在x0处单调递减，即若x在x0附近增大，则loss(x)将会减小。故我们将以一定的比率（即学习率）乘以梯度作为被减数，得到x的修改值。
具体原理参考链接
梯度下降（Gradient Descent）小结

二、使用步骤

1.如何用梯度下降求解线性方程组（预测线性函数）

当线性方程组有多于未知数个数的方程且具有噪声时，我们无法为其求得精确解。但我们要求线性函数的参数w，b，能够使得更多的点落在y=wx+b这条直线上，这样当我们在拥有一个x0，要预测其对应的y0时，就能确保这个预测的误差足够小。要达到这一点，就要求下图右边的loss函数最小。此时我们应该将loss函数对w和b求导。

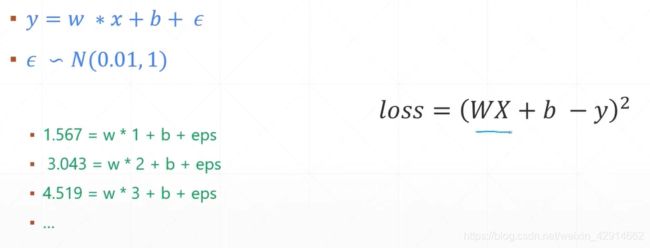
2.实战

代码如下（示例）：

# 求当前w,b下的loss
def compute_error_for_line_given_points(b,w,points):
    totalError=0
    for i in range(0,len(points)):
        x=points[i,0]
        y=points[i,1]
        totalError+=(y-(w*x+b))**2  #平方和
    return totalError/float(len(points))

# 求梯度
def step_gradient(b_current, w_current, points, learningRate):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        b_gradient += -(2 / N) * (y - ((w_current * x) + b_current))  # 求导取平均
        w_gradient += -(2 / N) * x * (y - ((w_current * x) + b_current))
    new_b = b_current - (learningRate * b_gradient)
    new_w = w_current - (learningRate * w_gradient)
    return [new_b, new_w]

#梯度下降函数
def gradient_decent_runner(points,starting_b,starting_m,learning_rate,num_iterations)
    b=starting_b
    m=starting_m
    for i in range(num_iterations):
        b,m=step_gradient(b,m,np.array(points),learning_rate)
    return [b,m]

接着用numpy生成需要的数据

def run():
    points = np.genfromtxt('./datasets/l3_data.csv',delimiter = ',')    
    lr = 0.0001
    initial_b = 0
    initial_w = 0
    iterations = 1000
    print(f"Starting project descent at b = {initial_b}, w = {initial_w},error = {compute_error_for_line_given_points(initial_b,initial_w,points)}")
    print('\nRunning...')
    [b,w] = gradient_descent_runner(points,initial_b,initial_w,lr,iterations)
    print(f"\nAfter project descent at b = {b}, w = {w},error = {compute_error_for_line_given_points(b,w,points)}")
    print('\nb:{}，w:{}'.format(b, w))

if __name__ == '__main__':
    run()

---

总结

结果可见线性回归问题