网络骨架:Backbone(神经网络基本组成——BN层、全连接层)
BN层
为了追求更高的性能,卷积网络被设计得越来越深,然而网络却变得难以训练收敛与调参。原因在于,浅层参数的微弱变化经过多层线性变化与激活函数后会被放大,改变了每一层的输入分布,造成深层的网络需要不断调整以适应这些分布变化,最终导致模型难以训练收敛
由于网络中参数变化导致的内部节点数据分布发生变化的现象被称作ICS(Internal Covariate Shift)。ICS现象更容易使训练过程陷入饱和区,减慢网络的收敛。ReLU从激活函数的角度出发,在一定程度上解决了梯度饱和的现象,而2015年提出的BN层,则从改变数据分布的角度避免了参数陷入饱和区。由于BN层优越的性能,其已经是当前卷积网络中的“标配”
BN层首先对每一个batch的输入特征进行白化操作,即去均值方差过程。假设一个batch的输入为x:B={x_1,… …,x_m},首先求该batch数据的均值和方差,如下面两个公式:
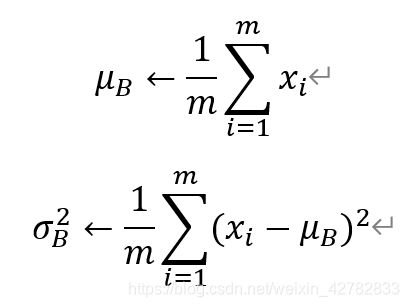
以上公式中,m代表batch的大小,μ_B为批处理数据的均值,σ_B^2为批处理数据的方差。在求得均值方差后,利用下面的式子进行去均值方差操作:
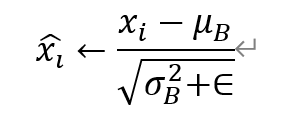
白化操作可以使输入的特征分布具有相同的均值与方差,固定了每一层的输入分布,从而加速网络的收敛。然而,白化操作虽然从一定程度上避免了梯度饱和,但也限制了网络中数据的表达能力,浅层学到的参数信息会被白化操作屏蔽掉,因此BN层在白化操作后又增加了一个线性变换操作,让数据尽可能地回复本身的表达能力,如上面的公式(去均值方差操作)和下面的公式:
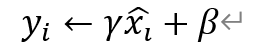
上面的公式中,γ与β为新引进的可学习参数,最终的输出为y_i
BN层可以看做是增加了线性变换的白化操作,在实际工程中被证明了能够缓解神经网络难以训练的问题。BN层的有点主要有以下三点:
- 缓解梯度消失,加速网络收敛。BN层可以让激活函数的输入数据落在非饱和区,缓解了梯度消失问题。此外由于每一层数据的均值与方差都在一定范围内,深层网络不必去不断适应浅层网络输入的变化,实现了层间耦合,允许每一层独立学习,也加快了网络的收敛
- 简化调参,网络更稳定。在调参时,学习率调的过大容易出现震荡与不收敛,BN层则抑制了参数微小变化随网络加深而被放大的问题,因此对于参数变化的适应能力更强,更容易调参
- 防止过拟合。BN层将每一个batch的均值与方差引入到网络中,由于每个batch的这两个值都不同,可看作为训练增加了随机噪音,可以起到一定的正定效果
在测试时,由于是对单个样本进行测试,没有batch的均值与方差,通常做法是在训练时将每一个batch的均值与方差都保留下来,在测试时使用所有训练样本均值与方差的平均值
PyTorch中使用BN层很简单,示例如下:
>>> from torch import nn
>>> #使用BN层需要传入一个参数为num_features,即特征的通道数
>>> bn = nn.BatchNorm2d(64)
>>> #eps为公式中的∈,momentum为均值方差的动量,affine为添加学习参数
>>> bn
BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
>>> input = torch.randn(4,64,224,224)
>>> output = bn(input)
>>> #BN层不改变输入、输出的特征大小
>>> output.shape
torch.Size([4, 64, 224, 224])
尽管BN层取得了巨大成功,但仍有一定的弊端,主要体现在以下两点:
- 由于实在batch的维度进行归一化,BN层要求较大的batch才能有效地工作,而物体检测等任务由于内存占用较高,限制了batch的大小,这会限制BN层有效地发挥归一化功能
- 数据的batch大小在训练与测试时往往不一样。在训练时一般采用滑动来计算平均值与方差,在测试时直接拿训练集的平均值与方差来使用。这种方式会导致测试集依赖于训练集,然而有时训练集与测试集的数据分布并不一致
因此,我们能不能避开batch来进行归一化呢?答案是可以的,最新的工作GN(Group Normalization)从通道方向计算均值与方差,使用更为灵活有效,避开了batch大小对归一化的影响
具体来讲,GN现将特征图的通道分为很多个组,对每一组内的参数做归一化,而不是batch。GN之所有能够工作的原因,笔者(董洪义)认为是在特征图中,不同的通道代表了不同的意义,例如形状、边缘和纹理等,这些不同的通道并不是完全独立地分布,而是可以放到一起进行归一化分析
全连接层
全连接层(Fully Connected Layers)一般连接到卷积网络输出的特征图右面,特点是每一个节点都与上下层的所有节点相连,输入与输出都被延展成一维向量,因此从参数量来看全连接层的参数量是最多的,如下图:
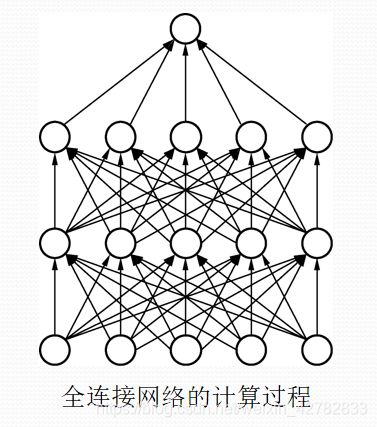
在物体检测算法中,卷积网络的主要作用是从局部到整体地提取图像的特征,而全连接层则用来将卷积抽象出的特征图进一步映射到特定维度的标签空间,以求取损失或者输出预测结果
PyTorch使用全连接层需要指定输入的与输出的维度,示例如下:
>>> import torch
>>> from torch import nn
>>> #第一维表示一共有4个样本
>>> input = torch.randn(4,1024)
>>> linear = nn.Linear(1024,1024)
>>> output = linear(input)
>>> input.shape
torch.Size([4, 1024])
>>> output.shape
torch.Size([4, 1024])
>>> input
tensor([[-2.4623, 0.6084, 0.3751, ..., 0.7292, -1.2410, -1.6428],
[-0.4258, -1.8207, 1.2047, ..., 0.2094, 0.2228, -0.1704],
[ 0.4121, 0.5616, -0.4086, ..., -0.5723, -0.3105, -1.5135],
[ 0.9815, 1.5876, -0.9927, ..., -1.7118, -0.3033, -0.8145]])
>>> output
tensor([[-1.0001, -0.5290, -1.2824, ..., -0.5184, 0.4400, -0.0543],
[-0.1626, 0.7201, 1.0155, ..., -0.7753, -0.5088, -0.1986],
[-0.0704, 0.1415, 0.2757, ..., 0.5789, -0.1673, 0.6739],
[-0.2043, -0.6982, 0.5784, ..., -0.2158, 0.2089, -0.1931]],
grad_fn=<AddmmBackward>)
然而,随着深度学习算法的发展,全连接层的缺点也逐渐暴露出来,最致命的问题在于其参数数量庞大。在此以VGGNet为例说明,其第一个全连接层的输入特征为77512=25088个节点,输出特征是大小为4096的一维向量,由于输出层的每一个点都来自于上一层所有点的权重相加,因此这一层的参数为250884096≈10^8。相比之下,VGGNet最后一个卷积层的卷积核大小为33512512≈2400000,全连接层的参数量是这一个卷积层的40多倍
大量的参数会导致网络模型应用部署困难,并且其中存在这大量参数冗余,也容易发生过拟合的现象。在很多场景中,我们可以使用全局平均池化层(Global Average Pooling,GAP)来取代全连接层,这种思想最早见于NIN(Network in Network)网络中,总体上,使用GAP有如下点好处:
- 利用池化实现了降维,极大地减少了网络的参数量
- 将特征提取与分类合二为一,一定程度上的防止过拟合
- 由于去除了全连接层,可以实现任意图像尺寸的输入