python二叉树遍历_先序中序后序_深度优先广度优先_非递归先序非递归中序
目录:
总代码:
python 二叉树广度优先遍历:
python 二叉树深度优先遍历:
先序遍历:
中序遍历:
后序遍历:
非递归的先序遍历:
非递归的中序遍历:
总代码:
class Node:
def __init__(self,data):
self.data = data
self.lchild = None
self.rchild = None
class Tree:
def __init__(self):
self.root = None
def add(self,data):
node = Node(data)
if self.root is None:
self.root = node
return
queue = [self.root]
while queue:
cur_node = queue.pop(0)
if cur_node.lchild is None:
cur_node.lchild = node
return
else:
queue.append(cur_node.lchild)
if cur_node.rchild is None:
cur_node.rchild = node
return
else:
queue.append(cur_node.rchild)
def breadth_travel(self):
"""广度遍历"""
if self.root == None:
return
queue=[self.root]
while queue:
cur_node = queue.pop(0)
print(cur_node.data,end=" ")
if cur_node.lchild is not None:
queue.append(cur_node.lchild)
if cur_node.rchild is not None:
queue.append(cur_node.rchild)
def dfs(self,root):
if root is None:
return
print(root.data)
self.dfs(root.left)
self.dfs(root.right)
def preorder(self, root):
"""先序遍历"""
if root is None:
return
print(root.data, end=" ")
self.preorder(root.lchild)
self.preorder(root.rchild)
def inorder(self, root):
"""中序遍历"""
if root is None:
return
self.inorder(root.lchild)
print(root.data, end=" ")
self.inorder(root.rchild)
def postorder(self, root):
"""后序遍历"""
if root is None:
return
self.postorder(root.lchild)
self.postorder(root.rchild)
print(root.data, end=" ")
def no_preorder(self,root):
"""非递归的先序遍历"""
if root==None:
return
alist=[root]
while alist:
cur=alist.pop()
print(cur.data)
if cur.rchild != None:
alist.append(cur.rchild)
if cur.lchild != None:
alist.append(cur.lchild)
def no_inorder(self,root):
cur=root
alist=[]
while cur or alist:
if cur!=None:
alist.append(cur)
cur=cur.lchild
else:
cur=alist.pop()
print(cur.data)
cur=cur.rchild
def same_tree(t1,t2):
"""两棵树相似"""
if t1==None and t2==None:
return True
if t1==None and t2!=None:
return False
if t1!=None and t2==None:
return False
# if t1.data!=t2.data:
# return False
else:
like_l=same_tree(t1.lchild,t2.lchild)
like_r=same_tree(t1.rchild,t2.rchild)
return (like_l and like_r)
if __name__=="__main__":
tree=Tree()
tree.add(0)
tree.add(1)
tree.add(2)
tree.add(3)
tree.add(4)
tree.add(5)
tree.add(6)
tree.add(7)
tree.add(8)
tree.add(9)
print("广度优先遍历")
tree.breadth_travel()
print("")
print("先序遍历")
tree.preorder(tree.root)
print("")
print("中序遍历")
tree.inorder(tree.root)
print("")
print("后序遍历")
tree.postorder(tree.root)
print("")
# tree2=Tree()
# tree2.add(0)
# tree2.add(1)
# tree2.add(2)
# # tree.add(3)
# # tree.add(4)
# # tree.add(5)
# # tree.add(6)
# # tree.add(7)
# # tree.add(8)
# # tree.add(9)
# print(same_tree(tree.root,tree2.root))
# tree.no_preorder(tree.root)
tree.no_preorder(tree.root)
print("...........................")
tree.no_inorder(tree.root)python 二叉树广度优先遍历:
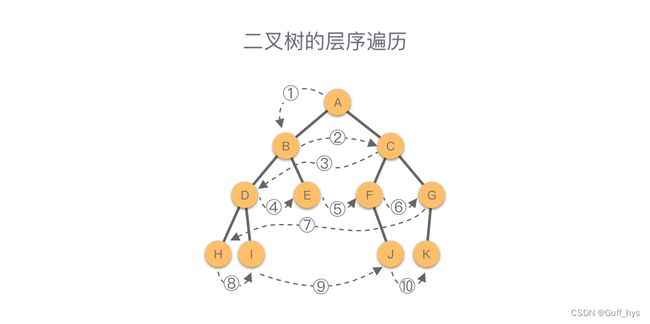
广度优先遍历(BFS)是一种用于遍历树或图的算法,它从根节点开始,逐层遍历每个节点的所有子节点。在二叉树中,广度优先遍历按照从上到下、从左到右的顺序遍历节点。
在Python中,可以使用队列来实现二叉树的广度优先遍历。具体步骤如下:
- 创建一个空队列,并将根节点加入队列中。
- 从队列中取出一个节点,并访问该节点。
- 将该节点的左子节点和右子节点(如果存在)依次加入队列中。
- 重复步骤2和步骤3,直到队列为空。
下面是一个示例代码,实现了二叉树的广度优先遍历:
def breadth_travel(self):
"""广度遍历"""
if self.root == None:
return
queue=[self.root]
while queue:
cur_node = queue.pop(0)
print(cur_node.data,end=" ")
if cur_node.lchild is not None:
queue.append(cur_node.lchild)
if cur_node.rchild is not None:
queue.append(cur_node.rchild)python 二叉树深度优先遍历:
在Python中,二叉树的深度优先遍历(DFS)有三种常见的方式:前序遍历、中序遍历和后序遍历。
- 前序遍历(Preorder Traversal):先访问根节点,然后递归地前序遍历左子树,最后递归地前序遍历右子树。
- 中序遍历(Inorder Traversal):先递归地中序遍历左子树,然后访问根节点,最后递归地中序遍历右子树。
- 后序遍历(Postorder Traversal):先递归地后序遍历左子树,然后递归地后序遍历右子树,最后访问根节点。
以下是一个示例代码,演示了如何实现二叉树的深度优先遍历:
先序遍历:
二叉树的先序遍历是指先访问根节点,然后递归地先序遍历左子树,最后递归地先序遍历右子树。具体步骤如下:
1. 访问根节点
2. 递归地先序遍历左子树
3. 递归地先序遍历右子树
这样就可以按照根节点、左子树、右子树的顺序遍历整棵二叉树。
def preorder(self, root):
"""先序遍历"""
if root is None:
return
print(root.data, end=" ")
self.preorder(root.lchild)
self.preorder(root.rchild)中序遍历:
二叉树的中序遍历是指先递归地中序遍历左子树,然后访问根节点,最后递归地中序遍历右子树。具体步骤如下:
1. 递归地中序遍历左子树
2. 访问根节点
3. 递归地中序遍历右子树
这样就可以按照左子树、根节点、右子树的顺序遍历整棵二叉树。
def inorder(self, root):
"""中序遍历"""
if root is None:
return
self.inorder(root.lchild)
print(root.data, end=" ")
self.inorder(root.rchild)后序遍历:
二叉树的后序遍历是指先递归地后序遍历左子树,然后递归地后序遍历右子树,最后访问根节点。具体步骤如下:
1. 递归地后序遍历左子树
2. 递归地后序遍历右子树
3. 访问根节点
这样就可以按照左子树、右子树、根节点的顺序遍历整棵二叉树。
def postorder(self, root):
"""后序遍历"""
if root is None:
return
self.postorder(root.lchild)
self.postorder(root.rchild)
print(root.data, end=" ")
非递归的先序遍历:
非递归的先序遍历可以使用一个辅助栈来实现,而不是使用列表。不过,如果一定要使用列表来实现非递归的先序遍历,可以模拟栈的操作。
具体步骤如下:
1. 创建一个空列表作为栈。
2. 将根节点压入栈中。
3. 循环执行以下步骤,直到栈为空:
a. 弹出栈顶节点,访问该节点。
b. 如果该节点的右子节点不为空,则将右子节点压入栈中(注意先压入右子节点,再压入左子节点)。
c. 如果该节点的左子节点不为空,则将左子节点压入栈中。
这样就可以使用列表来模拟栈的操作,实现非递归的先序遍历。
def no_preorder(self,root):
"""非递归的先序遍历"""
if root==None:
return
alist=[root]
while alist:
cur=alist.pop()
print(cur.data)
if cur.rchild != None:
alist.append(cur.rchild)
if cur.lchild != None:
alist.append(cur.lchild)非递归的中序遍历:
非递归的中序遍历可以使用一个辅助栈来实现,而不是使用列表。不过,如果一定要使用列表来实现非递归的中序遍历,可以模拟栈的操作。
具体步骤如下:
1. 创建一个空列表作为栈。
2. 将根节点压入栈中。
3. 循环执行以下步骤,直到栈为空:
a. 将当前节点的左子节点依次压入栈中,直到最左侧的叶子节点。
b. 弹出栈顶节点,访问该节点。
c. 将当前节点指向右子节点,重复步骤a。
这样就可以使用列表来模拟栈的操作,实现非递归的中序遍历。
def no_inorder(self,root):
cur=root
alist=[]
while cur or alist:
if cur!=None:
alist.append(cur)
cur=cur.lchild
else:
cur=alist.pop()
print(cur.data)
cur=cur.rchild