NUAA数据融合实验课报告
数据融合实验报告
聚类算法-K-means
1.算法原理
概念
K-均值(K-Means)算法是典型的基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。
K个初始聚类中心点的选取对聚类结果具有较大的影响,因为在该算法第一步中是随机地选取任意k个对象作为初始聚类中心,初始地代表一个簇。该算法在每次迭代中对数据集中剩余的每个对象,根据其与各个簇中心的距离赋给最近的簇。当考查完所有数据对象后,一次迭代运算完成,新的聚类中心被计算出来。
时间复杂度
O ( t k n m ) O(tknm) O(tknm)
其中,t 为迭代次数,k 为簇的数目,n 为样本点数,m 为样本点维度。
空间复杂度
O ( m ( n + k ) ) O(m(n+k)) O(m(n+k))
其中,k 为簇的数目,m 为样本点维度,n 为样本点数。
2.实验内容
了解K-均值算法,加强对非监督学习算法的理解和认识。采用开源代码,了解其算法思想,通过控制变量法探讨迭代次数n和分类数K的取值对实验结果的影响。找到分类结果收敛的最小n值和最合适的分类数目K值。
3.实验环境
- Windows10操作系统
- Python 3.8
- PyCharm工作台
4.实验结果
-
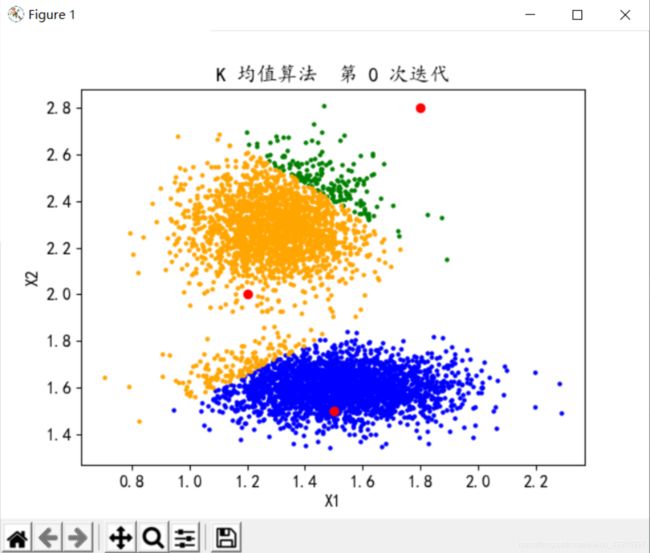
迭代次数n的讨论
分类数K=3,迭代次数n=2

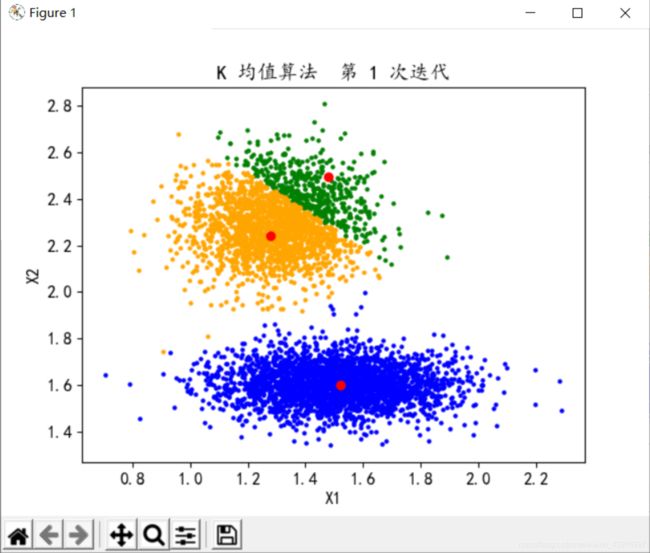
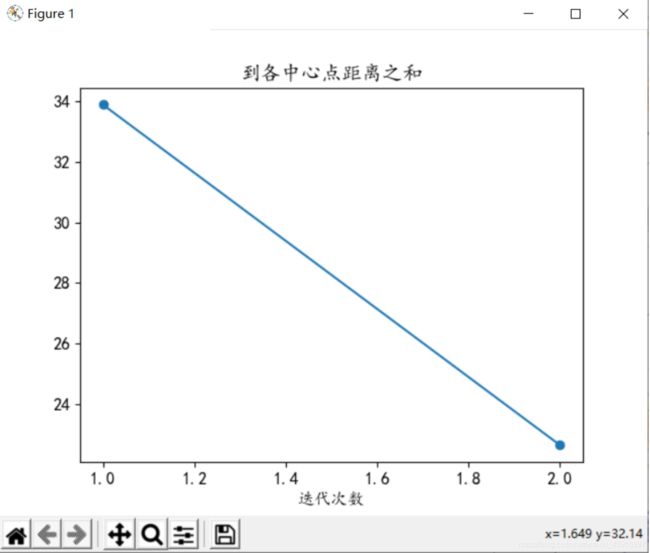
-
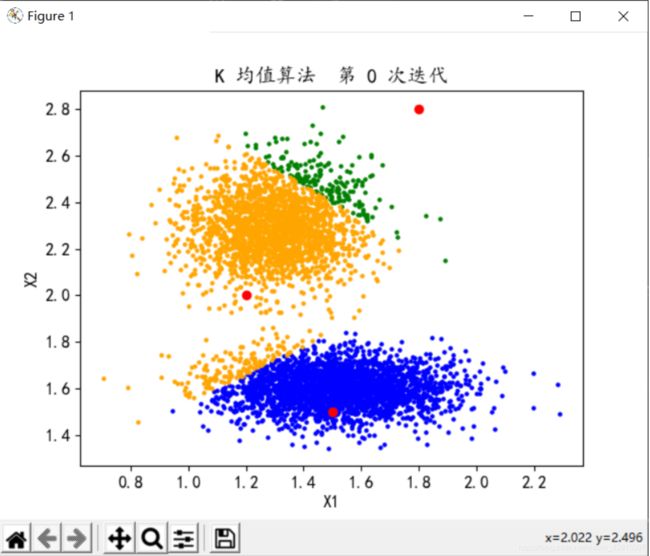
分类数K的讨论
迭代次数n=3,分类数K=2

迭代次数n=3,分类数K=3
5.分析讨论
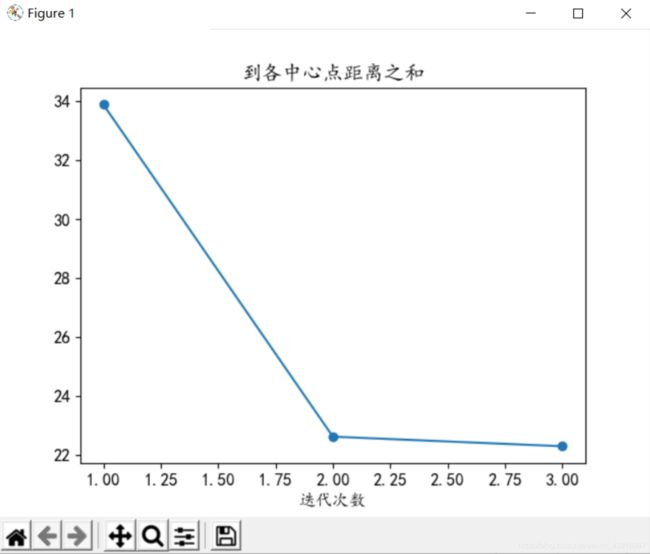
1、分析可知,迭代次数当增大到一定值后,聚类中心不发生变化,分类结果已经收敛,很多时候我们可能不必跑到最终结果,因此可以选择此时的n为迭代次数,大概就是折线图的折点,多于n消耗更多的性能,小于n结果可能并未达到理想条件。本案例中在n等于3-5时,聚类中心基本不再改变,因此可取n为3-5。算法逻辑简单,处理数据时具有可伸缩性和高效性。
2、对应本例的数据集,通过对比分类数K的值,可以得出结论:当分类数K=2时,类之间的区别更加明显,此时分类效果最好。所以说,分类数K值的选取需要一定的考虑。在大多数情况下,K值是未预先定义的,因此许多场景下K-均值算法并没有办法进行下去。但是,也有一些改进方法,对于可以确定K值不会太大但不明确精确的K值的场景,可以进行迭代运算,然后找出Cost Function最小时所对应的K值,这个值往往能较好的描述有多少个簇类。
6.个人感想
K-均值算法让我对无监督算法有了一定的了解。无监督的训练样本没有标签信息。K-均值算法原理和实现还是相对简单的,调参也方便些,并且可解释度强。在一些情况下,达到最优分类效果,则需要跑到分类结果完全收敛,此时调节类别K即可。当类别K确定时,调节迭代次数n可找到最优的折点。但是同样存在着缺点,K值不好选取,手动调节也无法证明哪个K是最优的。采用迭代也只是局部最优。对于噪音和异常点比较敏感。
我对算法的学习了解只是九牛一毛,未来学习的路还有很长,还是需要一步一个脚印的走下去!
分类算法-SVM与Adaboost的对比
1.概念先知
人脸识别
人脸识别是基于人的脸部特征信息进行身份识别的一种生物识别技术。用摄像机或摄像头采集含有人脸的图像或视频流,并自动在图像中检测和跟踪人脸,进而对检测到的人脸进行脸部识别的一系列相关技术,通常也叫做人像识别、面部识别。
SVM支持向量机
支持向量机(support vector machines, SVM)是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM还包括核技巧,这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题,也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。
核心思想
- 它是针对线性可分情况进行分析,对于线性不可分的情况,通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分,从而使得高维特征空间采用线性算法对样本的非线性特征进行线性分析成为可能。
- 它基于结构风险最小化理论之上再特征空间中构建最优超平面,使得学习器得到全局最优化,并且在整个样本空间的期望以某个概率满足一定上界。
Adaboost自适应提升算法
Adaboost是一种迭代算法,其核心思想是针对同一个训练集训练不同的分类器(弱分类器),然后把这些弱分类器集合起来,构成一个更强的最终分类器(强分类器)。对AdaBoost算法的研究以及应用大多集中于分类问题,同时也出现了一些在回归问题上的应用。就其应用AdaBoost系列主要解决了: 两类问题、多类单标签问题、多类多标签问题、大类单标签问题、回归问题。它用全部的训练样本进行学习。
核心思想
- 初始化所有样本的权重,让所有样本的权重的初始值相等。
- 用样本的一个子集来创建一个弱分类器(比如一棵决策树)。
- 用刚创建的弱分类器,对所有的样本进行预测,获得预测结果。
- 增大预测错误的样本的权重。
- 在更新了权重的样本上创建第二个弱分类器。
- 依此类推,继续创建若干个弱分类器,直至新创建的弱分类器的精度不再变化,或者达到了弱分类器数目的上限。
- 把上面生成的弱分类器组合成一个强分类器。
2.实验内容
采用PCA特征提取,SVM和Adaboost方法进行LFW (Labled Faces in the Wild)数据集人脸分类识别实验。利用人脸识别实验,进行量化后,通过准确率以及混淆矩阵等指标进行算法模型的评价和对比。
3.实验环境
- Windows10操作系统
- Python 3.8
- PyCharm工作台
4.实验结果
SVM
![]()
一些特征脸以及部分预测结果图
![]()
预测结果
| precision | recall | f1-score | support | |
|---|---|---|---|---|
| Colin Powell | 0.94 | 0.94 | 0.94 | 64 |
| Donald Rumsfeld | 0.96 | 0.84 | 0.90 | 32 |
| George W Bush | 0.88 | 0.97 | 0.92 | 127 |
| Gerhard Schroeder | 1.00 | 0.86 | 0.93 | 29 |
| Tony Blair | 0.93 | 0.82 | 0.87 | 33 |
| accuracy | 0.92 | 285 | ||
| macro avg | 0.94 | 0.89 | 0.91 | 285 |
| weighted avg | 0.92 | 0.92 | 0.92 | 285 |
混淆矩阵
60 0 4 0 0 0 27 4 0 1 4 0 123 0 0 0 0 3 25 1 0 1 5 0 27 \begin{matrix} 60&0&4&0&0\\ 0&27&4&0&1\\ 4&0&123&0&0\\ 0&0&3&25&1\\ 0&1&5&0&27\\ \end{matrix} 6004000270014412335000250010127
Adaboost
![]()
预测结果
| precision | recall | f1-score | support | |
|---|---|---|---|---|
| Ariel Sharon | 1.00 | 0.15 | 0.27 | 13 |
| Colin Powell | 0.81 | 0.72 | 0.76 | 60 |
| Donald Rumsfeld | 0.62 | 0.37 | 0.47 | 27 |
| George W Bush | 0.68 | 0.94 | 0.79 | 146 |
| Gerhard Schroeder | 0.79 | 0.44 | 0.56 | 25 |
| Hugo Chavez | 0.67 | 0.13 | 0.22 | 15 |
| Tony Blair | 0.61 | 0.56 | 0.58 | 36 |
| accuracy | 0.70 | 322 | ||
| macro avg | 0.74 | 0.47 | 0.52 | 322 |
| weighted avg | 0.71 | 0.70 | 0.67 | 322 |
混淆矩阵
2 2 3 6 0 0 0 0 43 0 15 0 0 2 0 1 10 14 1 0 1 0 2 3 137 1 0 3 0 2 0 7 11 1 4 0 1 0 8 1 2 3 0 2 0 14 0 0 20 \begin{matrix} 2&2&3&6&0&0&0\\ 0&43&0&15&0&0&2\\ 0&1&10&14&1&0&1\\ 0&2&3&137&1&0&3\\ 0&2&0&7&11&1&4\\ 0&1&0&8&1&2&3\\ 0&2&0&14&0&0&20\\ \end{matrix} 2000000243122123010300061514137781400111110000012002134320
5.分析讨论
根据预测矩阵可分析,人脸预测的准确率,SVM>Adaboost。 Adaboost识别 率比不上SVM可能是由于Adaboost需求的数据集更大。两者各有缺陷,于是引发猜想将两者结合,提出一-种使用SVM作为Adaboost的弱分类器的算法,去提高分类精度,这样我相信性能会大大提升。在知网找了找类似的论文和期刊,发现已经有人提出设想并付出实践了,而且很巧的是其中一篇期刊1还是南航的民航学院发的,测试结果相对于SVM和Adaboost提高了很多,结果证明猜想是正确的。
6.个人感想
通过学习SVM, Adaboost两个算法,简单的了 解了有监督学习算法。有监督学习将包含特征和标签信息的样本作为训练样本,通过训练样本训练得到一一个最优模型,再利用这个模型将所有的输入映射为相应的输出,对输出进行简单的判断从而实现预测和分类的目的,也就具有了对未知数据进行预测和分类的能力。
对于开源代码,由于没有基础,很难读懂,不知道怎样去改代码从而实现自己想要的功能。在查阅许多资料和讲义后,渐渐了解了其中的意义。通过修改代码,进行一定的实验验证,得到了自己想要的答案。算法的学习过程是长远的,不能松懈。但我相信通过这门课还是对算法有了一定的了解,有了这种基本思想,在未来碰到相近的问题就会想到类似的解决办法。虽然对分类的理解越来越清晰,但还是有许多分类算法没有触及到的,像随机森林,神经网络等等,我打算在这个暑假的实习之余在算法算法这个方面好好入个门,去深学一下。
优化算法-Simulated Annealing算法
1.算法原理
概念
模拟退火算法来源于固体退火原理,是一种基于概率的算法,将固体加温至充分高,再让其徐徐冷却,加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。模拟退火算法是通过赋予搜索过程一种时变且最终趋于零的概率突跳性,从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。
算法思想
- 初始化:初始温度T(充分大),初始解状态S(是算法迭代的起点),每个T值的迭代次数L
- 对k=1, …, L做第3至第6步:
- 产生新解S′
- 计算增量ΔT=C(S′)-C(S),其中*C(S)*为评价函数
- 若ΔT<0则接受*S′作为新的当前解,否则以概率exp(-ΔT/T)接受S′*作为新的当前解.
- 如果满足终止条件则输出当前解作为最优解,结束程序。终止条件通常取为连续若干个新解都没有被接受时终止算法。
- T逐渐减少,且T->0,然后转第2步。
2.实验内容
通过模拟退火算法求解函数极小值。在此基础上分析初始温度、退火速度等对实验结果的影响。
3.实验环境
- Windows10操作系统
- Python 3.8
- PyCharm工作台
4.实验结果
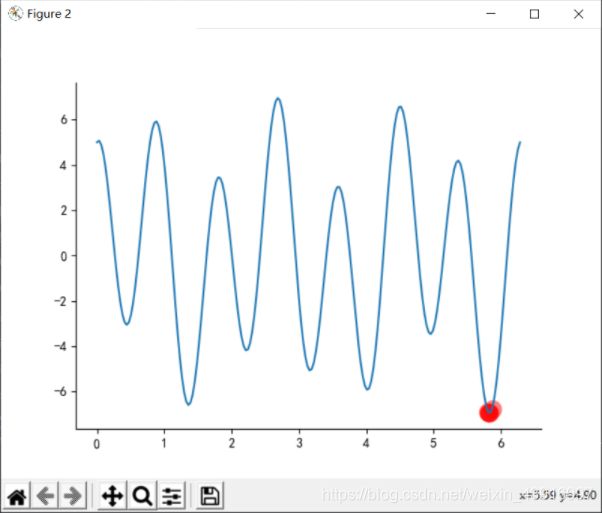
优化函数
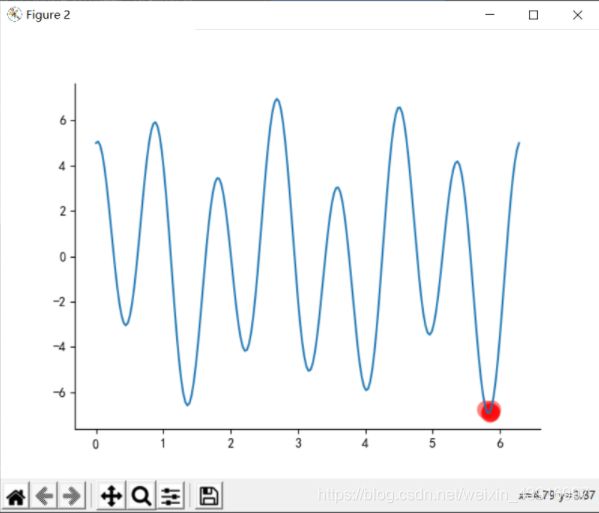
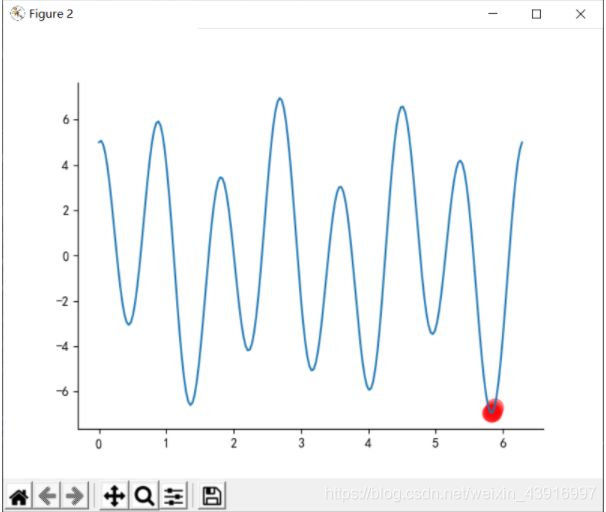
f ( x ) = 2 s i n 3 x + 5 c o s 7 x f(x)=2sin3x + 5cos7x f(x)=2sin3x+5cos7x
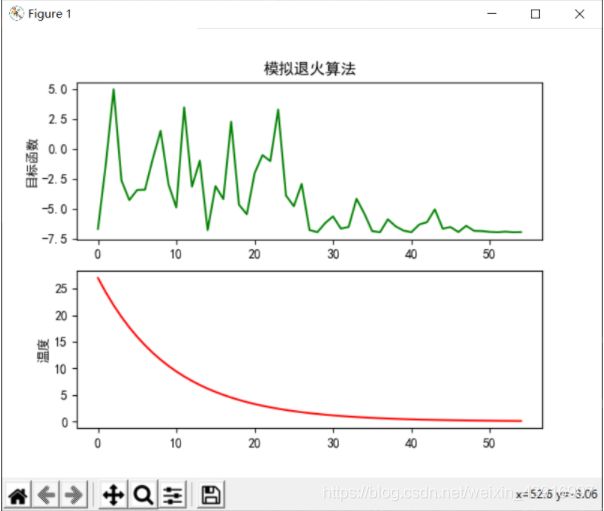
保持其他参数为定值,探究初始温度的影响结果
T = 5


| 平均极小值 | 最优极小值 | 最差极小值 | 时间 | |
|---|---|---|---|---|
| 初始温度T=5 | -6.923147016535256 | -6.95151972310965 | -6.852209494501508 | 8.106 |
| 初始温度T=10 | -6.909866465244906 | -6.95324035183279 | -6.832837098973896 | 8.382 |
| 初始温度T=30 | -6.844884682866477 | -6.98808195479659 | -6.754096287888009 | 8.886 |
保持其他参数为定值,探究退火速度对实验结果的影响
R = 0.85
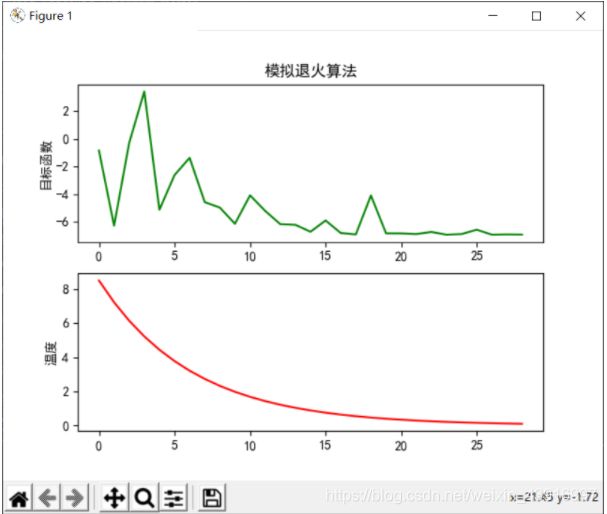
| 平均极小值 | 最优极小值 | 最差极小值 | 时间 | |
|---|---|---|---|---|
| 退火速度R=0.8 | -6.863179503674246 | -6.988212015771716 | -6.677351848507188 | 7.371 |
| 退火速度R=0.85 | -6.903378493966993 | -6.952597616324424 | -6.839439531282712 | 7.390 |
| 退火速度R=0.9 | -6.856913290366973 | -6.951020710386369 | -6.718120583762075 | 7.417 |
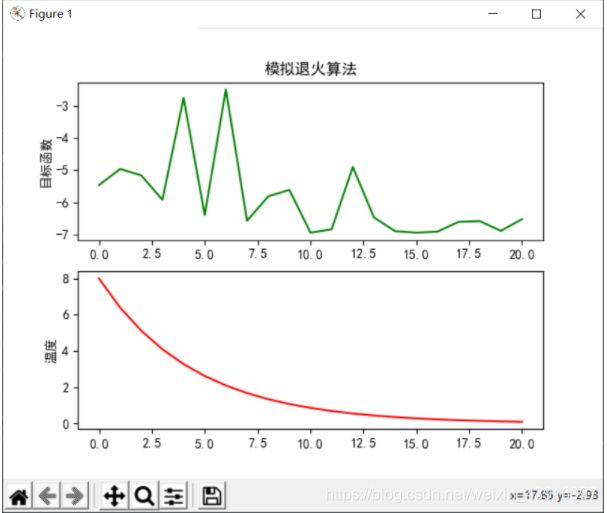
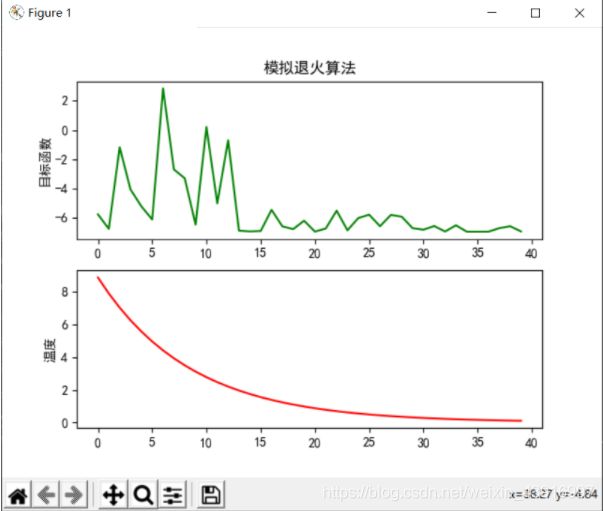
5.分析讨论
通过实验可以发现,模拟退火算法计算过程比较简单,且鲁棒性强,多次实验都能达到较好的结果,统计结果都有较好的表现。但是由表格我们也发现了一些缺点,如下:
-
对于退火温度:当温度下降较快,也就是退火速度较快时,很容易得到的不是全局最优解。而我们为了得到全局最优解,就要使温度下降的足够慢,以进行全局搜索,这样会导致执行时间比较长,带来开销的增大。
-
对于初始温度:温度T的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一、初始温度高,则搜索到全局最优解的可能性大,但因此要花费大量的计算时间;反之,则可节约计算时间,但全局搜索性能可能受到影响。
因此一个性能优良的退火算法模型需要经过我们反复的调参,知道找到一个相对合适的参数集合,这样才会得到我们想要的结果。
6.个人感想
模拟退火算法作为一种经典算法,有其独特的好处,对于一般的优化问题,其都能得到比较好的优化结果,具有较强的通用性。因此,复杂的算法并不一定是好的,相反,一些简单的算法,稍加变形,将可以在多个问题上表现出较好的结果。
在学习的过程中,碰到无法理解的知识,就去Google或者知网查相关的论文解释,弄懂后才去进行下一步。学习的过程就是这样。后面我会继续学习算法,争取让自己的知识储备更广,让自己的视野更加开阔!