openCV c++基于LBP特征向量的SVM的车牌分类
目录
-
- 一、背景
- 二、环境及GitHub下载地址:
- 三、SVM简介
-
- 3.1、学习样本和类别标签处理
- 3.2、设置模型类别、训练参数
- 3.3、训练模型
- 3.4、评估模型
- 四、LBP简介
-
- 4.1、基本的LBP算子
- 4.2、圆形的LBP算子
- 4.3、LBP等价模式
- 4.4、LBP特征向量
- 五、运行结果
- 六、参考资料
一、背景
在openCV车牌识别的实战项目中,对车牌的提取不可能做到百分之百准确,往往存在多个非车牌区域,此时需要对提取到的所有区域进行分类,找到真正的车牌区域。openCV集成了SVM支持向量机分类算法,这里就训练一个SVM模型对车牌进行分类。
二、环境及GitHub下载地址:
编译器:vs2019
环境:OpenCV3.4.4
工程文件GitHub链接:链接
三、SVM简介
SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。主要步骤包括:
1. 训练样本及其类别标签处理。
2.设置模型类别、训练参数。
3.训练模型。
4.评估模型。
3.1、学习样本和类别标签处理
输入层为训练集需要将训练数据存储为cv :: Mat对象的CV_32FC1类型,且为n行m列(n为训练集数量,m为单个样本的像素数量),每一行对应一个样本,所以需要将样本转换为一行;输出层为训练集标签需要存储为cv :: Mat对象的CV_32SC1类型,且为n行1列(n为训练集数量),每行与训练样本的类别标签一一对应。
定义训练集及标签:
//训练集
Mat trainMat = Mat::zeros(trainNum, lbpNum*4*17, CV_32FC1);
//训练集标签
Mat trainLabel = Mat::zeros(trainNum, 1, CV_32SC1);
读取训练集及标签:
void readImage(const string path, Mat inputImg, Mat label)
{
Mat lbpImg;
int n = 0;
for (int i = 0; i < 2; i++)
{
char folder[100];
if (i == 0)
{
//负样本
sprintf_s(folder, "%s/%s", path.c_str(), "no");
}
else
{
//正样本
sprintf_s(folder, "%s/%s", path.c_str(), "has");
}
vector<cv::String> imagePathList;
//读取路径下所有图片
glob(folder, imagePathList);
for (int j = 0; j < imagePathList.size(); j++)
{
int radius, neighbors;
//假设
radius = 1; //半径越小 图像越清晰 精细
neighbors = 8; //领域数目越小,图像亮度越低,合理,4太小了比较黑 设置8比较合理
//读取图片
auto img = imread(imagePathList[j]);
//标签图像第n行的首地址
int* labelPtr = label.ptr<int>(n);
//标签图像赋值
labelPtr[0] = i;
Mat lbpImg = Mat(imgRows, imgCols, CV_8UC1, Scalar(0));
//转换成灰度图
cvtColor(img, img, COLOR_BGR2GRAY);
//调整大小
Mat shrink;
resize(img, shrink, Size(imgCols + 2 * radius, imgRows + 2 * radius), 0, 0, CV_INTER_LINEAR);
//提取lbp特征
elbp(shrink, lbpImg, 1, 8);
//提取特征向量
Mat m = getLBPH(lbpImg, lbpNum, 17, 4, false);
m.row(0).copyTo(inputImg.row(n));
n++;
//imshow("img", lbpImg);
//waitKey(0);
}
}
}
这里将训练样本的LBP特征向量作为输入层,关于LBP后面介绍。
3.2、设置模型类别、训练参数
设置SVM的模型类型,其中SVC是分类模型,SVR是回归模型:
svm->setType(SVM::C_SVC);
设置核函数,数据由低维空间转换到高维空间后运算量会呈几何级增加,
支持向量机能够通过核函数有效地降低计算复杂度。
svm->setKernel(SVM::LINEAR);
核函数类别:
2.POLY(多项式核):

3.RBF(RBF核):

4.SIGMOID(SIGMOID核):
5.指数和Histogram intersection核 :

由核函数的定义可以知道不同核函数需要调整的参数:
//阶数针对POLY核函数
svm->setDegree(0);
//针对RBF和POLY核函数
svm->setGamma(0);
//偏移量针对POLY核函数
svm->setCoef0(0);
//惩戒因子
svm->setC(0.1);
//模型型别参数
svm->setNu(0);
svm->setP(0);
//终止条件最小误差
svm->setTermCriteria(TermCriteria(CV_TERMCRIT_EPS, 1000, 0.05));
其中cv::TermCriteria::TermCriteria(int _type, int _maxCount, double _epsilon)参数说明:
_type:CV_TERMCRIT_EPS:终止条件最小误;CV_TERMCRIT_ITER :终止条件最大迭代次数。
_maxCount:最大迭代次数
_epsilon:最小误差
3.3、训练模型
//训练
svm->train(trainMat, ROW_SAMPLE, trainLabel);
//保存模型
svm->save("svm.xml");
3.4、评估模型
int testNum;
//测试集路径
string testPath = "C:/Users/Tiam/Desktop/classify/image/classify_test";
//测试集数量
testNum = getNum(testPath);
//测试集
Mat testMat = Mat::zeros(testNum, lbpNum * 4 * 17, CV_32FC1);
//测试集标签
Mat testLabel = Mat::zeros(testNum, 1, CV_32SC1);
//读取
readImage(testPath, testMat, testLabel);
int count = 0;
string modelPath = "C:/Users/Tiam/Desktop/classify/svm.xml";
Ptr<ml::SVM>svmpre = ml::SVM::load(modelPath);
cout << "开始预测" << endl;
for (int i = 0; i < testNum; i++)
{
Mat img;
testMat.row(i).copyTo(img);
int result;
result = svmpre->predict(img);
if (result == testLabel.at<int>(i, 0))
{
count++;
}
}
cout << "预测完成" << endl;
cout << "正确率:" << (float)count / (float)testNum << endl;
四、LBP简介
LBP(Local Binary Pattern,局部二值模式)是一种用来描述图像局部纹理特征的算子;它具有旋转不变性和灰度不变性等显著的优点。
LBP特征向量提取步骤:
1. 获取图像的LBP特征;
2. 将LBP图像划分为多个小区域;
3. 计算每个小区域的直方图;
4. 讲各个区域的直方图连接,得到LBP特征向量。
4.1、基本的LBP算子
原始的LBP算子定义在像素33的邻域内,以邻域中心像素为阈值,相邻的8个像素的灰度值与邻域中心的像素值进行比较,若周围像素大于中心像素值,则该像素点的位置被标记为1,否则为0。这样,33邻域内的8个点经过比较可产生8位二进制数,将这8位二进制数依次排列形成一个二进制数字,这个二进制数字就是中心像素的LBP值,LBP值共有256种可能。中心像素的LBP值反映了该像素周围区域的纹理信息。
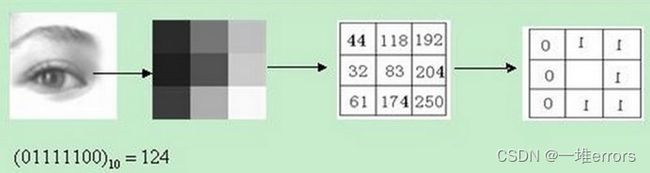
4.2、圆形的LBP算子
基本的 LBP 算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域,这显然不能满足不同尺寸和频率纹理的需要。为了适应不同尺度的纹理特征,并达到灰度和旋转不变性的要求,Ojala 等对 LBP 算子进行了改进,将 3×3 邻域扩展到任意邻域,并用圆形邻域代替了正方形邻域,改进后的 LBP 算子允许在半径为 R 的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子;
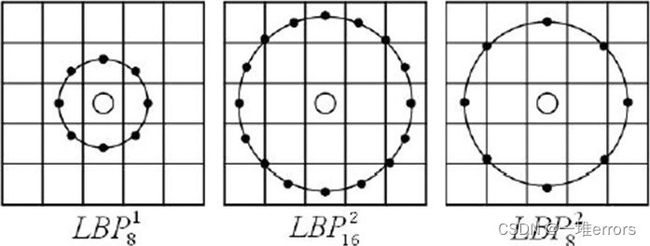
//2.圆形算子LBP函数
//src:输入图像
//dst:输出图像
//radius:半径
//neighbors:要处理周围像素点的数量
void elbp(Mat& src, Mat& dst, int radius, int neighbors)
{
for (int n = 0; n < neighbors; n++)
{
// 采样点的计算
float x = static_cast<float>(radius * cos(2.0 * CV_PI * n / static_cast<float>(neighbors)));
float y = static_cast<float>(-radius * sin(2.0 * CV_PI * n / static_cast<float>(neighbors)));
// 上取整和下取整的值
int fx = static_cast<int>(floor(x));
int fy = static_cast<int>(floor(y));
int cx = static_cast<int>(ceil(x));
int cy = static_cast<int>(ceil(y));
// 小数部分
float ty = y - fy;
float tx = x - fx;
// 设置插值权重
float w1 = (1 - tx) * (1 - ty);
float w2 = tx * (1 - ty);
float w3 = (1 - tx) * ty;
float w4 = tx * ty;
// 循环处理图像数据
for (int i = radius; i < src.rows - radius; i++)
{
for (int j = radius; j < src.cols - radius; j++)
{
// 计算插值
float t = static_cast<float>(w1 * src.at<uchar>(i + fy, j + fx) + w2 * src.at<uchar>(i + fy, j + cx) + w3 * src.at<uchar>(i + cy, j + fx) + w4 * src.at<uchar>(i + cy, j + cx));
// 进行编码
dst.at<uchar>(i - radius, j - radius) += ((t > src.at<uchar>(i, j)) || (std::abs(t - src.at<uchar>(i, j)) < std::numeric_limits<float>::epsilon())) << n;
}
}
}
}
4.3、LBP等价模式
很显然,随着邻域集内采样点数的增加,二进制模式的种类是以指数形式增加的。例如:5×5邻域内20个采样点,有 =1,048,576种二进制模式。这么多的二进制模式不利于纹理的提取、分类、识别及存取。例如,将LBP算子用于纹理分类或人脸识别时,常采用LBP模式的统计直方图来表达图像的信息,而较多的模式种类将使得数据量过大,且直方图过于稀疏。因此,需要对原始的LBP模式进行降维,使得数据量减少的情况下能最好的表示图像的信息。
为了解决二进制模式过多的问题,提高统计性,Ojala提出了采用一种“等价模式”(Uniform Pattern)来对LBP算子的模式种类进行降维。Ojala等认为,在实际图像中,绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。因此,Ojala将“等价模式”定义为:当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时,该LBP所对应的二进制就称为一个等价模式类。如00000000(0次跳变),00000111(只含一次从0到1的跳变),10001111(先由1跳到0,再由0跳到1,共两次跳变)都是等价模式类。除等价模式类以外的模式都归为另一类,称为混合模式类,例如10010111(共四次跳变)。通过这样的改进,二进制模式的种类大大减少,而不会丢失任何信息。模式数量由原来的 种减少为 P ( P-1)+2种,其中P表示邻域集内的采样点数。对于3×3邻域内8个采样点来说,二进制模式由原始的256种减少为58种,即:它把值分为59类,58个uniform pattern为一类,其它的所有值为第59类。这样直方图从原来的256维变成59维。这使得特征向量的维数更少,并且可以减少高频噪声带来的影响。
//等价模式LBP特征计算
//src:输入图像
//dst:输出图像
//radius:半径
//neighbors:要处理周围像素点的数量
void getUniformPatternLBPFeature(Mat src, Mat dst, int radius, int neighbors)
{
//LBP特征图像的行数和列数的计算要准确
dst.create(src.rows - 2 * radius, src.cols - 2 * radius, CV_8UC1);
dst.setTo(0);
//LBP特征值对应图像灰度编码表,直接默认采样点为8位
uchar temp = 1;
uchar table[256] = { 0 };
for (int i = 0; i < 256; i++)
{
if (getHopTimes(i) < 3)
{
table[i] = temp;
temp++;
}
}
//是否进行UniformPattern编码的标志
bool flag = false;
//计算LBP特征图
for (int k = 0; k < neighbors; k++)
{
if (k == neighbors - 1)
{
flag = true;
}
//计算采样点对于中心点坐标的偏移量rx,ry
float rx = static_cast<float>(radius * cos(2.0 * CV_PI * k / neighbors));
float ry = -static_cast<float>(radius * sin(2.0 * CV_PI * k / neighbors));
//为双线性插值做准备
//对采样点偏移量分别进行上下取整
int x1 = static_cast<int>(floor(rx));
int x2 = static_cast<int>(ceil(rx));
int y1 = static_cast<int>(floor(ry));
int y2 = static_cast<int>(ceil(ry));
//将坐标偏移量映射到0-1之间
float tx = rx - x1;
float ty = ry - y1;
//根据0-1之间的x,y的权重计算公式计算权重,权重与坐标具体位置无关,与坐标间的差值有关
float w1 = (1 - tx) * (1 - ty);
float w2 = tx * (1 - ty);
float w3 = (1 - tx) * ty;
float w4 = tx * ty;
//循环处理每个像素
for (int i = radius; i < src.rows - radius; i++)
{
for (int j = radius; j < src.cols - radius; j++)
{
//获得中心像素点的灰度值
uint8_t center = src.at<uint8_t>(i, j);
//根据双线性插值公式计算第k个采样点的灰度值
float neighbor = src.at<uint8_t>(i + x1, j + y1) * w1 + src.at<uint8_t>(i + x1, j + y2) * w2 \
+ src.at<uint8_t>(i + x2, j + y1) * w3 + src.at<uint8_t>(i + x2, j + y2) * w4;
//LBP特征图像的每个邻居的LBP值累加,累加通过与操作完成,对应的LBP值通过移位取得
dst.at<uchar>(i - radius, j - radius) |= (neighbor > center) << (neighbors - k - 1);
//进行LBP特征的UniformPattern编码
if (flag)
{
dst.at<uchar>(i - radius, j - radius) = table[dst.at<uchar>(i - radius, j - radius)];
}
}
}
}
}
//计算跳变次数
int getHopTimes(int n)
{
int count = 0;
bitset<8> binaryCode = n;
for (int i = 0; i < 8; i++)
{
if (binaryCode[i] != binaryCode[(i + 1) % 8])
{
count++;
}
}
return count;
}
"getUniformPatternLBPFeature"函数将LBP算子从0-255映射到0-59,其中跳变次数大于三次的归为0这一种模式。注意:这段代码默认邻域像素点数量为8个,如果采用其它数量的邻域像素点需要修改 uchar table[256] = { 0 };数组的大小及 int getHopTimes(int n)函数的循环条件等。
4.4、LBP特征向量
一般不直接将LBP图像作为特征检测的输入,而是将LBP的特征向量作为特征检测的输入。
//计算LBP特征图像的直方图LBPH
//src为LBP是通过lbp计算得到的
//numPatterns为计算LBP的模式数目,一般为2的幂
//grid_x和grid_y分别为每行或每列的block个数
//normed为是否进行归一化处理,1:归一化,0:进行归一化
Mat getLBPH(Mat src, int numPatterns, int grid_x, int grid_y, bool normed)
{
int width = src.cols / grid_x;
int height = src.rows / grid_y;
//定义LBPH的行和列,grid_x*grid_y表示将图像分割成这么些块,numPatterns表示LBP值的模式种类
Mat result = Mat::zeros(grid_x * grid_y, numPatterns, CV_32FC1);
if (src.empty())
{
return result.reshape(1, 1);
}
int resultRowIndex = 0;
//对图像进行分割,分割成grid_x*grid_y块,grid_x,grid_y默认为8
for (int i = 0; i < grid_y; i++)
{
for (int j = 0; j < grid_x; j++)
{
//图像分块
Mat src_cell = Mat(src, Range(i * height, (i + 1) * height), Range(j * width, (j + 1) * width));
//计算直方图
Mat hist_cell = getLocalRegionLBPH(src_cell, 0, (numPatterns - 1), normed);
//将直方图放到result中
Mat rowResult = result.row(resultRowIndex);
hist_cell.reshape(1, 1).convertTo(rowResult, CV_32FC1);
resultRowIndex++;
}
}
return result.reshape(1, 1);
}
//计算一个LBP特征图像块的直方图
Mat getLocalRegionLBPH(const Mat& src, int minValue, int maxValue, bool normed)
{
//定义存储直方图的矩阵
Mat result;
//计算得到直方图bin的数目,直方图数组的大小
int histSize = maxValue - minValue + 1;
//定义直方图每一维的bin的变化范围
float range[] = { static_cast<float>(minValue),static_cast<float>(maxValue + 1) };
//定义直方图所有bin的变化范围
const float* ranges = { range };
//计算直方图,src是要计算直方图的图像,1是要计算直方图的图像数目,0是计算直方图所用的图像的通道序号,从0索引
//Mat()是要用的掩模,result为输出的直方图,1为输出的直方图的维度,histSize直方图在每一维的变化范围
//ranges,所有直方图的变化范围(起点和终点)
calcHist(&src, 1, 0, Mat(), result, 1, &histSize, &ranges, true, false);
//归一化
if (normed)
{
result /= (int)src.total();
}
//结果表示成只有1行的矩阵
return result.reshape(1, 1);
}
参数说明:
numPatterns为计算LBP的模式数目,实际为划分区域直方图的维数,一般为2的幂,这里使用八邻域的圆形算子,所以LBP的模式数目为256,如果采用八邻域的等价模式LBP算子则模式数目为59。
grid_x和grid_y分别为每行或每列的block个数,这里将图像分为了4×17块,每块区域直方图的维数为numPatterns,所以最后得到的特征向量维数为numPatterns × 4 × 17(即训练集的列数)。
//训练集
Mat trainMat = Mat::zeros(trainNum, lbpNum*4*17, CV_32FC1);
五、运行结果
准确率在99%以上。
六、参考资料
1. SVM相关代码来自:这里
2. 关于LBP原理参考自:这里
3. LBP实现代码来自:这里
4. 所用数据集来自:这里
如有侵权联系马上修改,本人能力有限,如有错误欢迎评论指正,完整代码前往前文的GitHub地址下载


