作者导读:Inner-IoU:基于辅助边框的IoU损失
论文地址:
Inner-IoU: More Effective Intersection over Union Loss with Auxiliary Bounding Box
视频讲解
代码
摘要:
随着检测器的迅速发展, 边框回归取得了巨大的进步。然而,现有的基于 IoU 的边框回归仍聚焦在通过加入新的损失项来加速收敛,忽视 IoU 损失项其自身的限制。尽管理论上 IoU 损失能够有效描述边框回归状态,在实际应用中,它无法根据不同检测器与检测任务进行自我调整,不具有很强的泛化性。基于以上,我们首先分析了 BBR 模式,得出结论在回归过程区分不同回归样本并且使用不同尺度的辅助边框计算损失能够有效加速边框回归过程。对于高 IoU 样本,使用较小的辅助边框计算损失能够加速收敛,而较大辅助边框适用于低 IoU 样本。接着,我们提出了 Inner-IoU Loss, 其通过辅助边框计算 IoU 损失。针对不同的数据集与检测器,我们引入尺度因子 ratio 控制辅助边框的尺度大小用于计算损失。最后,将 Inner-IoU 集成至现有的基于 IoU 损失函数中进行仿真实验与对比实验。实验结果表明在使用本文所提出方法后检测效果得到进一步提升,验证了本文方法的有效性以及泛化能力。
贡献:
• 我们分析边框回归过程与模式,基于边框回归问题自身特性,提出在模型训练过程中使用较小的辅助边框计算损失对高IoU 样本的回归有增益效果,低IoU样本则与之相反。
• 我们提出了Inner-IoU Loss ,使用尺度因子ratio控制生成不同尺度的辅助边框用于计算损失。将其应用至现有IoU-based 损失函数中能够获得更快更为有效的回归结果。
• 我们进行了一系列仿真实验与对比实验,实验结果表明本文方法的检测效果与泛化性优于现有方法,并且适用于不同尺度的数据集达到了SOTA。
方法:
1.边框回归模式分析
IoU 损失函数在计算机视觉任务中具有广泛的应用。在边框回归过程中不但能够评估回归状态的好坏,而且能够通过计算回归损失进行梯度传播从而加速收敛。在这我们讨论回归过程中IoU 变化与边框尺寸的关系,分析边框回归问题的自身特性,解释本文所提出方法的合理性。
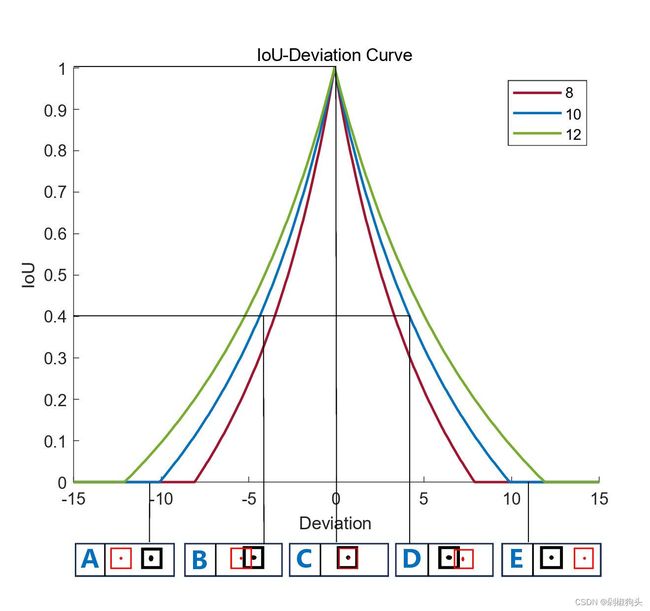 图1(a)
图1(a) 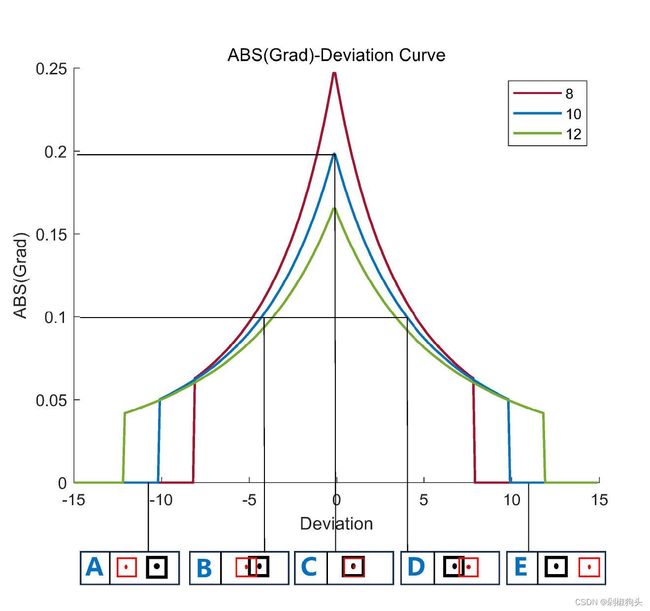 图1(b)
图1(b)
如上图所示,其中图1.a 为IoU-Deviation 曲线图,其水平轴与竖直轴分别表示deviation与IoU 值,三种不同颜色曲线对应不同尺度边框的IoU 变化曲线。A,B,C,D,E 分别对应achors and GT 框5 种不同位置关系,其中红色边框代表长宽为10 的anchors, 其对应的GT 框用黑色边框表示。图1.b 为ABS(Grad)-Deviation 曲线图,与图1.a 所不同的是在图1.b 中纵轴表示IoU 梯度的绝对值。我们假设实际边框尺寸为10,尺寸为8 和12 的边框作为其辅助边框。在图a与图b 中A,E 对应低IoU 样本回归状态,B,D 对应高IoU 样本回归状态,由图1可以得到以下结论。
1. 由于辅助边框与实际边框之间仅存在尺度差异,在回归过程中其IoU 值的变化趋势与实际边框的IoU值变化趋势一致,能够反应实际边框回归结果的质量。
2. 对于高IoU 样本,较小尺度的辅助边框的IoU梯度的绝对值大于实际边框IoU 梯度的绝对值。
3. 对于低IoU 样本,较大尺度的辅助边框的IoU梯度的绝对值大于实际边框IoU 梯度的绝对值。基于以上分析,使用较小尺度的辅助边框计算IoU 损失将有助于高IoU 样本回归,达到加速收敛的效果。与之相反使用较大尺度的辅助边框计算IoU 损失能够加速低IoU 样本回归过程。
2. Inner-IOU Loss
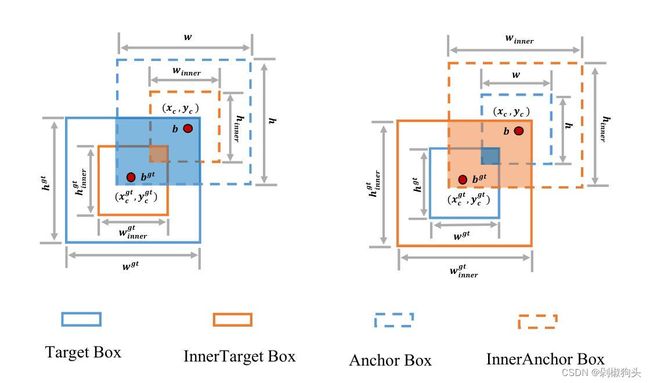
如图2所示,GT 框和锚框分别表示为![]() 和
和![]() 。GT框和GT 框内部的中心点用(
。GT框和GT 框内部的中心点用(![]() ,
,![]() ) 表示,而(
) 表示,而(![]() )则表示锚框和内部锚框的中心点。GT 框的宽度和高度分别表示为
)则表示锚框和内部锚框的中心点。GT 框的宽度和高度分别表示为![]() 和
和![]() ,而锚框的宽度和高度分别表示为w 和h。变量”ratio ” 对应的是尺度因子,通常取范围为[0.5,1.5]。Inner-IoU 的定义如下:
,而锚框的宽度和高度分别表示为w 和h。变量”ratio ” 对应的是尺度因子,通常取范围为[0.5,1.5]。Inner-IoU 的定义如下:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
Inner-IoU损失继承了IoU损失的一些特性,同时具有自身的特性。和IoU损失一样Inner-IoU损失的取值范围为[0,1]。因为辅助边框与实际边框仅存在尺度上的差异,损失函数计算方式相同,InnerIoU-Deviation 曲线与IoU-Deviation曲线相似。与IoU损失相比,当ratio小于1,辅助边框尺寸小于实际边框,其回归的有效范围小于IoU损失,但其梯度绝对值大于IoU损失所得的梯度,能够加速高IoU样本的收敛。与之相反,当ratio大于1,较大尺度的辅助边框扩大了回归的有效范围,对于低Iou的回归有所增益。将Inner-IoU应用至现有基于IoU的边框回归损失函数中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() 的定义如下:
的定义如下:
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
实验结果与分析:
1.仿真实验
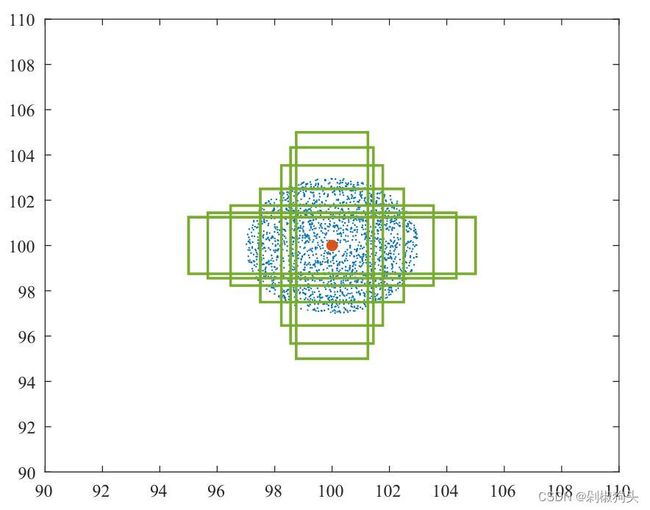 图3.a
图3.a 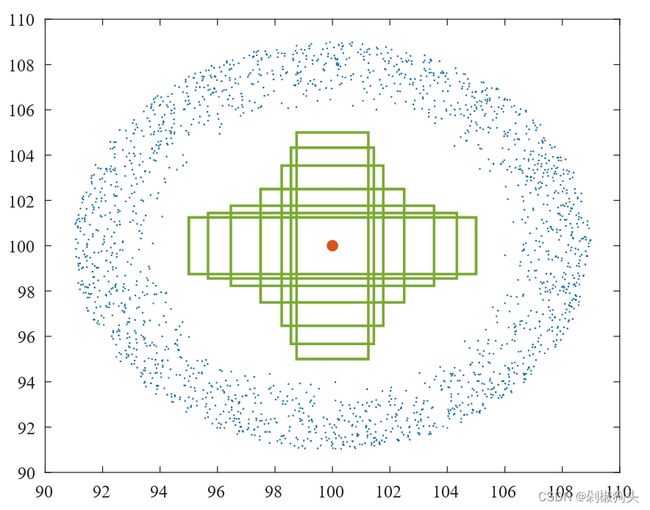 图3.b
图3.b
如图3所示,本文针对两种不同场景进行了边框回归的仿真实验,图3.a与图3.b分别对应高 IoU回归样本场景与低IoU回归样本场景。在图3.a与图3.b中7种不同形状大小的绿色边框表示GT框,其中心点坐标设为(100,100),长宽比率分别为1:4, 1:3, 1:2, 1:1, 2:1, 3:1, 4:1。图中蓝色斑点表示anchor的分布,如图3.a在以(100,100)为中心 3为半径随机分布着2000个anchor点,每个点位置上有49个anchor包括七种长宽比(i.e., 1:4, 1:3, 1:2, 1:1, 2:1, 3:1,4:1)与七种尺度(i.e., 0.5, 0.67,0.75, 1, 1.33, 1.5 ,2)。在图3.b中以(100,100)为中心,半径为6至9随机分布着2000个anchor点。最后,在每个仿真实验中,总计686000=7 × 7 ×7× 2000 个回归案例。
2.仿真实验结果
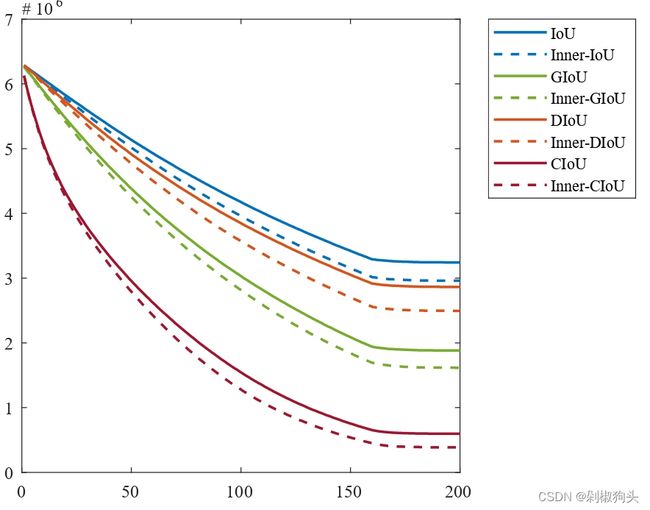 图4.a
图4.a 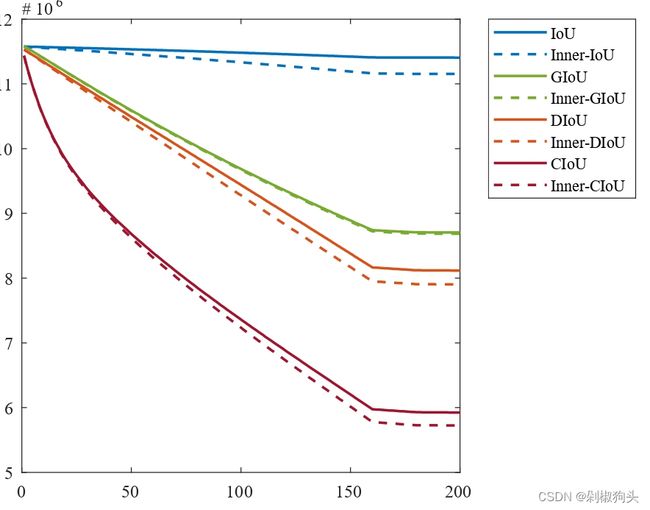 图4.b
图4.b
仿真实验的结果如图所示,其中图4.a表示高 IoU回归样本场景下的收敛结果,为了加速高IoU样本的回归,将尺度因子ratio设置为0.8。而低 IoU回归样本场景下的收敛结果如图4.b所示,将ratio设为1.2。可以看出图中虚线所代表的本文方法收敛速度优于现有的方法。
3.对比实验
YOLOv7 on PASCAL VOC
实验对比了CIoU方法与SIoU方法,使用yolov7-tiny作为检测器,VOC2007 trainval与VOC2012 trainval 作为训练集,VOC2007 test作为测试集。训练集包括16551张图像,测试集4952张图像包含20类。我们将训练集训练了150 epochs,为了展现本文方法的优越性。我们将本文方法与原始方法的训练过程可视化,如图5所示。
a b c
d e f
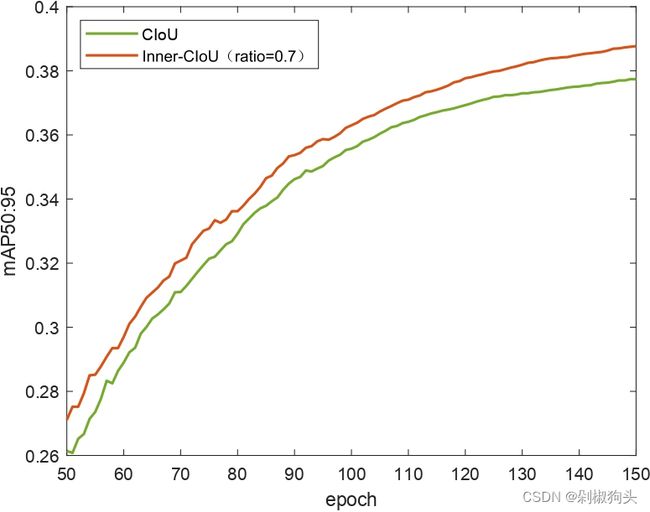
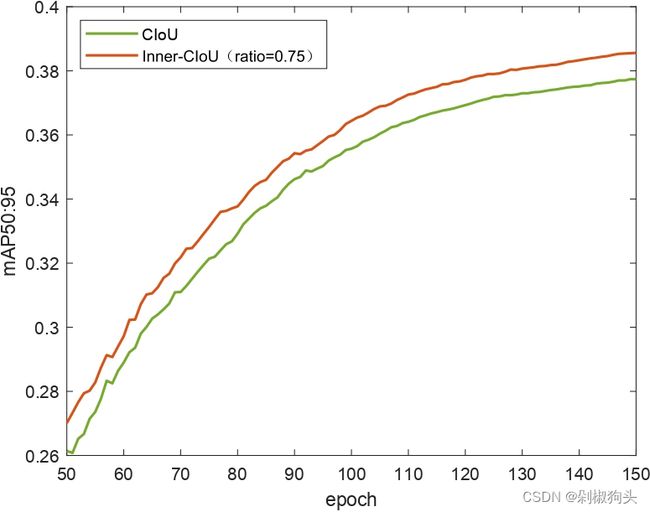
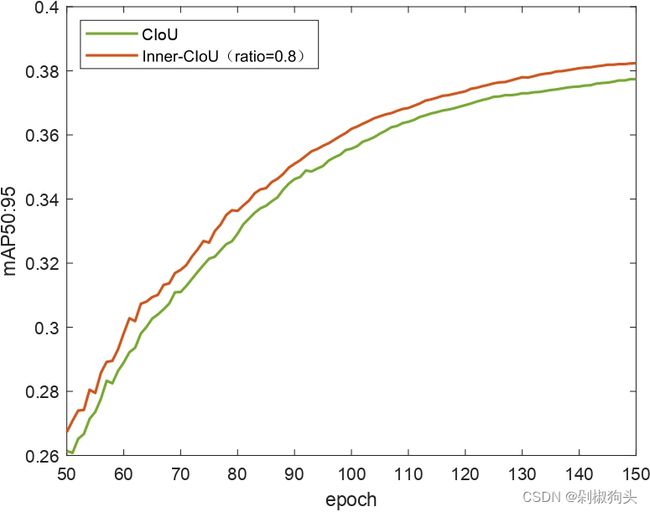
图5
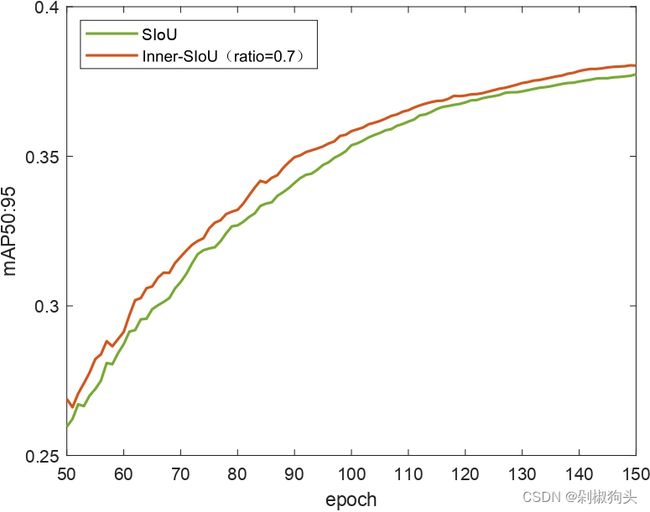
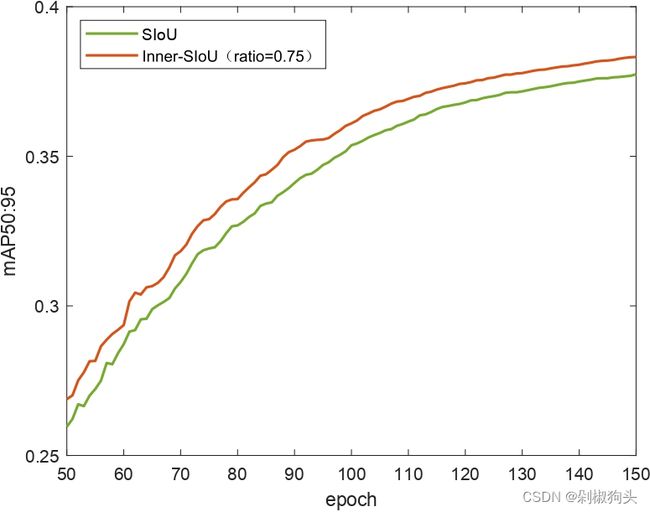
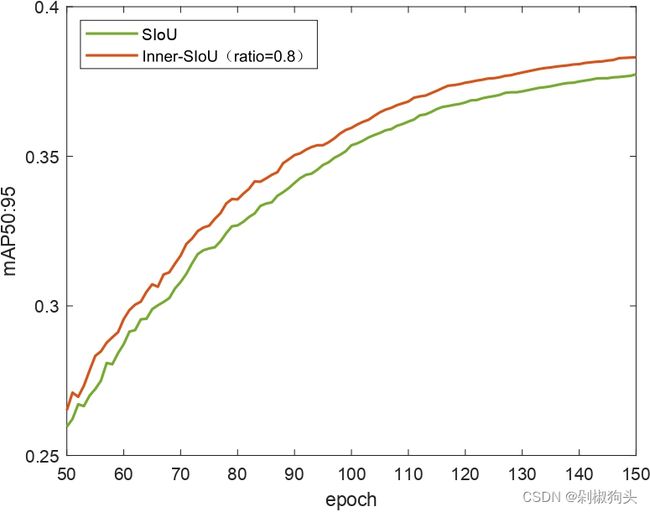
图5.a, 5.b和5.c 为CIoU and Inner-CIoU的训练过程曲线图,三张图分别对应ratio 为0.7, 0.75, and 0.8。图5.d, 图5.e和 图5.f 为ratio 分别为0.7, 0.75, and 0.8时,SIoU and Inner-SIoU的训练过程曲线图。在以上图中,橙色曲线代表本文方法,现有方法用绿色曲线表示。不难看出在训练过程中50至150 epochs 本文方法优于现有的方法。
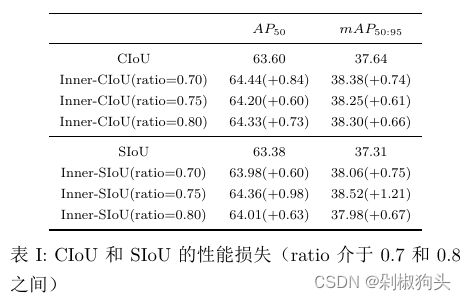
测试集对比实验结果如表1所示。可以看出,应用本文方法后,检测效果有所提高,AP50和mAP50:95提高了0.5%以上。图6和图7是检测样本的对比图。从图中可以看出,与现有方法相比,所提出的方法定位更准确,误检和漏检更少。
图6
图7
YOLOv5 on AI-TOD
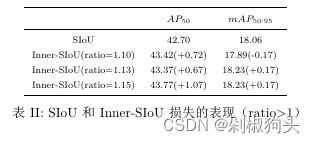
为了证明本文方法的泛化能力,我们使用yolov5s检测器在AI-TOD 数据集与进行了对比实验,实验选用SIoU作为对比方法。AI-TOD 包含28,036 aerial images包含8类目标以及700,621 object instances,其中14018张图像作为训练集, 另外的14018张图像作为测试集。与现有的目标检测任务数据集相比,AI-TOD的平均尺寸为12.8像素,远小于其他数据集。实验结果如表2所示。
在对比实验1,通过将ratio值设置0.7到0.8之间小于1,产生小于实际边框的辅助边框。实验结果证明其能够对高IoU样本产生增益。在实验2中ratio值大于1,通过生成较大得辅助边框达到对低IoU样本加速收敛的效果,另外,图8为在测试集上的检测效果对比图,通过对比可以看出本文方法的优越性。
图8
结论:
在本文,我们分析了边框回归过程并且指出IoU损失的限制,其对于不同的检测任务不具有很强的泛化性。基于边框回归问题的自身特性,我们提出了Inner-IoU一种基于辅助边框的边框回归损失。其通过尺度因子ratio控制辅助边框尺寸用于计算损失加速收敛。它能够集成至现有基于IoU的损失函数中达到SOTA。通过一系列仿真实验与消融实验,验证本文方法优于现有方法。值得一提的是,本文方法不但适用于一般的检测任务,对于极小目标的检测任务也表现良好,方法泛化性得到了验证。
讨论:
Q1:论文试图解决什么问题?
弥补现有IoU-baesd 边框回归损失泛化性不足。
Q2:这是否是一个新问题?
使用辅助边框计算边框回归损失,就本文作者所掌握的信息而言,是新的问题。
Q3:这篇文章要验证一个什么科学假设?
现有的IoU损失,可以看作是Inner-IoU中的尺度因子ratio为1的特殊情况,不具备泛化性。
Q4:有哪些相关研究?如何归类?
主流方法:IoU,GIoU,DIoU,CIoU,EIoU,SIoU
变体方法:Alpha-IoU,Wise-IoU
归类:边框回归
Q5:论文中提到的解决方案之关键是什么?
使用辅助边框
Q6:论文中的实验是如何设计的?
为了证明本文方法泛化性,使用多种检测器,多种数据集(不同尺度),多种对比方法。
Q7:用于定量评估的数据集是什么?代码有没有开源?
PASCAL VOC(2007+2012),AI-TOD
代码已开源
Q8:论文中的实验及结果有没有很好地支持需要验证的科学假设?
仿真实验与对比实验均已验证
Q9:这篇论文到底有什么贡献?
真正的贡献在于质疑原有使用实际边框计算IoU损失的合理性,并提出使用辅助边框的思路尝试去克服原有损失的不足,通过实验证明本文研究在2D水平框目标检测问题上有效,给予其他需要用到边框回归的研究提供启发。
Q10:下一步呢?有什么工作可以继续深入?
在目标检测领域,可以将本文的研究思路拓展到旋转框的目标检测,以及3D目标检测。