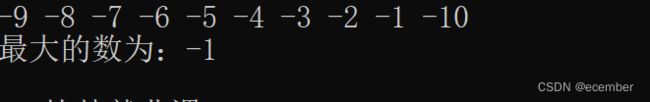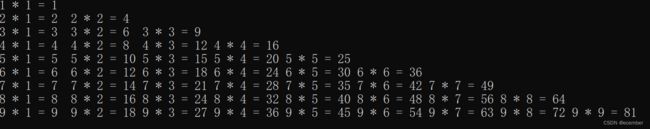【C语言经典好题笔记——(1)】
| 感谢大家的点赞 和关注 ,如果有需要可以看我主页专栏哟 |
文章目录
- ⚡1. 前言
- ⚡2. C经典题目讲解
-
- 2.1 将三个数由大到小输出
- 2.2 打印出1-100之间所有3的倍数
- 2.3 求两个数的最大公约数
- 2.4 素数求解
- 2.5 求1-100整数中出现多少个数字9
- 2.6 计算1/1 -1/2+1/3-1/4+1/5.....+ 1/99+1/100的值
- 2.7 求数组中十个元素最大值
- 2.8 在屏幕上输出乘法口诀表
- ⚡3. 递归大杂烩
-
- 3.1 求n的阶乘
- 3.2 求第n个斐波那契数
- ⚡6. 结语
⚡1. 前言
生命中最快乐的事情是拼搏,而非成功,生命中最痛苦的是懒散,而非失败。大家好,这里是ecember。今天ecember来带大家速刷C语言经典题目,部分题目包含优化算法与普通算法哟。(以下结果均在vs2022中编译)

⚡2. C经典题目讲解
这里将为大家讲解C语言经典题目。题目虽少但干货慢慢哦。
2.1 将三个数由大到小输出
本题要求我们输入三个数,并将其按由大到小的方式输出。ecember初学C语言的时候遇到这道题直接强行比较,大的先输出小的后输出,这样做太麻烦了呜呜。下面就是我初学时的冤种代码。
#include 大家千万不要这样做,不仅算法麻烦,效率低还容易出现bug,那么这里我们怎么搞呢?我们假设三个数a,b,c,我们既然不知道最大最小数,那么我们就随便一个a是最大的,b是最中间值,c是最小的。那么我们是不是应该把最大的放在a里以此类推,于是我们便有了以下想法:
<1>先拿a跟b比较,若a < b则a,b交换。
<2>再拿a跟c比较,若a < c则a,c交换。
<3>最后b跟c比较,若b < c则b,c交换。
1,2步我们就已经把最大值放在了a里面,然后第3步将中间值放在了b里面,剩下的c自然就是最小值。
#include 这里我们借用了函数那一章讲过的交换函数exchange,需要请移步【大战函数——将函数彻底吃透】,我们再来测试一下。

2.2 打印出1-100之间所有3的倍数
和打印偶数差不多的算法只要判断1-1001之家之间的数 %3是否等于0就OK了。
#include 说到这里看过我博客的小伙伴肯定已经想到了更巧妙的算法。以下即为优化算法
#include 2.3 求两个数的最大公约数
我们举个例子,比如24和18,如果要求这两个数的最大公约数,我们首先可能会想到不妨从18开始一个一个试直到,每试一次不符合条件被整除即减1,那么一直这样下去,跳出循环的那个数即为最大公约数。
int main()
{
int a = 0, b = 0;
int m = 0;
scanf("%d %d", &a, &b);
m = (a > b ? a : b);//将 m 置为a,b中较大的数
while (1)
{
if (a % m == 0 && b % m == 0)
{
break;
}
m--;
}
printf("%d\n", m);
return 0;
}

这种方法可能是我们能想到的最简单的方法了,但是效率不是很好,我们试想当两个数足够大时,我们需要循环很多次才能找到那个最大公约数,这样也就对我们的程序带来了压力,那么有什么效率高的算法吗?相信大家高中都学过更相减损术和辗转相除法吧。忘了的话也没关系,下面一一为大家介绍。
更相减损术
第一步:任意给定两个正整数;判断它们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止。
则第一步中约掉的若干个2的积与第二步中等数的乘积就是所求的最大公约数。其中所说的“等数”,就是公约数。求“等数”的办法是“更相减损”法。
代码实现
int main()
{
int a = 0, b = 0;
int m = 0, cnt = 0;
scanf("%d %d", &a, &b);
while (a % 2 == 0 && b % 2 == 0)
{
a = a / 2;
b = b / 2;
cnt++;
}
while (a != b)
{
if (a > b)
{
m = a - b;
a = b;
b = m;
}
else
{
m = b - a;
b = a;
a = m;
}
}
for (m = 0; m < cnt; m++)
{
a *= 2;
}
printf("%d\n", a);
return 0;
}
辗转相除法
辗转相除法的算法步骤为,两个数中用较大数除以较小数,再用出现的余数(第一余数)去除除数,再用出现的余数(第二余数)去除第一余数,如此反复,直到最后余数是0为止。得到最后的除数就是这两个数的最大公约数。
算法实现
int main()
{
int a = 0, b = 0;
int m = 0;
scanf("%d %d", &a, &b);
while (m = a % b)//不用比较a,b的大小,第二次循环就是交换后
{
a = b;
b = m;
}
printf("%d\n", b);
return 0;
}
拓展延伸
求最小公倍数算法。
int main()
{
int a = 0, b = 0;
int m = 0;
scanf("%d %d", &a, &b);
m = (a > b ? a : b);
while (1)
{
if (m % a == 0 && m % b == 0)
{
break;
}
m++;
}
printf("%d\n", m);
return 0;
}
原理跟方法1差不多。但这里有一个公式:
当我们知道两个数a,b的最大公倍数m时,其最大公约数为a * b / m。
算法实现
int MAX(int x, int y)
{
int m = 0;
while (m = x % y)
{
x = y;
y = m;
}
return y;
}
int main()
{
int a = 0, b = 0;
int m = 0;
scanf("%d %d", &a, &b);
printf("%d\n", a * b / MAX(a, b));//公式需要记住
return 0;
}
2.4 素数求解
传送门:素数求解的五大境界。
2.5 求1-100整数中出现多少个数字9
我们首先考虑哪些数字可能会出现9,首先是9,19,29…这一类数字,还有90,91…99(两个9)这一类数字。我们首先利用 %10得到1-100的个位数字,然后求出第一种情况中9的个数,再利用 /10得到第二种情况中9的个数,两次相加即可。
int main()
{
int i = 0;
int count1 = 0, count2 = 0;
for (i = 1; i <= 100; i++)
{
count1++;
if (i % 10 == 9)
{
count2++;
}
if (i / 10 == 9)
{
count2++;
}
}
printf("**************\n");
printf("循环次数:%d\n", count1);
printf("个数:%d\n", count2);
printf("**************\n");
}
2.6 计算1/1 -1/2+1/3-1/4+1/5…+ 1/99+1/100的值
这里我们首先观察分母为1-100逐级递增,那么我们是不是能用for循环了,此外这每一个数的符号都不一样,我们需要只做加法运行显然不行,那么我们试想既然要循环,我们每次借助这个循环来变号是不是就可以了呢。
int main()
{
int i = 0, x = 1;
double sum = 0;
for (i = 1; i <= 100; i++)
{
sum += 1.0 / i * x;
x = -x;
}
printf("%.8lf\n", sum);
return 0;
}
我们这里借助了一个辅助变量x来实现变号,同时观察结果一定是小数,所以我们的操作符“/”两端需进行浮点数运算。
2.7 求数组中十个元素最大值
这道题我们第一时间可能会觉得很简单,不就是求最大值吗,直接循环遍历数组,再随便指定个变量0,跟它比较。最后所得值不就是最大值吗?我们试试
int main()
{
int arr[11] = { 0 };
int i = 0, m = 0, n = 0;
for (i = 0; i < 10; i++)
{
scanf("%d", &arr[i]);
}
m = 0;
for (i = 0; i < 10; i++)
{
if (m < arr[i])
{
m = arr[i];
}
}
printf("最大的数为:%d\n", m);
return 0;
}
我们测试一组数据。
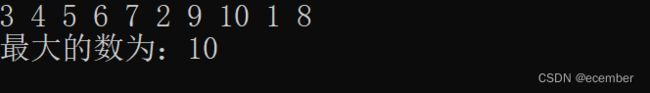
正确的啊,我们再来一组。

此处我们的程序就出现了bug,当数组元素全<0时,我们的结果就出现了错误,因此这个比较变量必须是我们数组内元素才可行。
int main()
{
int arr[11] = { 0 };
int i = 0, m = 0, n = 0;
for (i = 0; i < 10; i++)
{
scanf("%d", &arr[i]);
}
m = arr[0];//不能直接用 m = 0
for (i = 0; i < 10; i++)
{
if (m < arr[i])
{
m = arr[i];
}
}
printf("最大的数为:%d\n", m);
return 0;
}
2.8 在屏幕上输出乘法口诀表
乘法口诀表的格式相信大家都知道。

看这个样子肯定是要用循环了,我们观察到一共有9行,第1行有1列,第2行有2列,第3行有3列,细心的小伙伴已经发现了,每行的列数一定是小于等于行数的,因此我们采用嵌套for循环的结构。
int main()
{
int i = 0, j = 0;
for (i = 1; i <= 9; i++)
{
for (j = 1; j <= i; j++)
{
printf("%d * %d = %-2d ", i, j, i * j);//左对齐-2d,右对齐-2d
}
printf("\n");
}
return 0;
}

这打印出来一部分数字没有对齐,于是我们便使用一下%d的对齐方式,%-2d表示空两格左对齐,%2d表示空两格右对齐。应用一下。
⚡3. 递归大杂烩
这里我们刷几道函数递归的练习。
3.1 求n的阶乘
我们知道n的阶乘是n*(n-1)*…*1。既然我们要用递归我们就思考一下应该用那种递归,这题显然是要用return的递归,那么限制条件是什么呢?这里n肯定是要大于1才能继续递归,此外n每次递归都减1以更接近递归条件。
int fac(int n)
{
if (n <= 1)
{
return 1;
}
else
{
return n * fac(n - 1);
}
}
int main()
{
int m = 0;
scanf("%d", &m);
int ret = fac(m);
printf("\n%d\n", ret);
return 0;
}
3.2 求第n个斐波那契数
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N* ) 在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用,为此,美国数学会从 1963 年起出版了以《斐波纳契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。
由上述斐波那契数的定义,我们发现用递归来求解斐波那契数变得可行,限制条件即为n >= 2,用return来实现递归每次就用n-1和n-2来更接近限制条件。
int count = 0;
int fib(int n)
{
if (n <= 2)
{
return 1;
}
else
{
return fib(n - 1) + fib(n - 2);
}
}
int main()
{
int m;
scanf("%d", &m);
printf("%d\n", fib(m));
return 0;
}

这里一直不出答案啊,难道是编译器在偷懒吗?显然不是,你的光标在闪烁表明编译器已在疯狂运算,奈何计算量太庞大导致编译器系统都要算冒烟了还没算出来结果(这里博主亲自测试发现运算10分钟左右才能出答案)。我们不妨添加一个监视变量count来看看循环多少次。
int count = 0;
int fib(int n)
{
if (3 == n)
{
count++;
}
if (n <= 2)
{
return 1;
}
else
{
return fib(n - 1) + fib(n - 2);
}
}
int main()
{
int m;
scanf("%d", &m);
printf("%d\n", fib(m));
printf("%d\n", count);
return 0;
}

这里当n = 40是都递归了39088169次,那么当n = 50时估计人都比计算机算得快,所以这里用递归显然就不是最好的方法了。那还有其他方法吗?上述方法是由后向前计算,计算量过于庞大,我们能想到的是由前向后计算,计算量会少很多。我们这里用循环由前向后计算,求第多少个斐波那契数就循环多少次。
int fib(int n)
{
int a = 1;
int b = 1;
int c = 1;//n == 1/2时为1
while (n > 2)
{
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
int main()
{
int m;
scanf("%d", &m);
printf("%d\n", fib(m));
return 0;
}

这里斐波那契数第五十个数已经超过了我们的int类型最大值,故打印出来为错误结果,但是结果一编译就出来了,效率确实提高了很多。
⚡6. 结语
到这,我们的 《C语言刷题笔记——(1)》 已经接近尾声了,后续我还会持续更新C语言相关内容,学习永无止境,就会永远只会留给有准备的人。希望我的博客对大家有所帮助,如果喜欢的可以 点赞+收藏哦,也随时欢迎大家在评论区及时指出我的错误。