二叉树链式结构
前言:
想必大家看到本篇文章应该是对二叉树是有一定了解的,当然,如果不了解也没关系,我都会依次讲解的,如果有兴趣请看下去哦!
本片文章实现的是二叉树的链式结构,在对其操作的各个函数几乎都利用了递归逻辑,所以理解起来有一定的抽象。
1、二叉树的基本理论
二叉树的链式存储结构是指用链表表示一颗二叉树,即用链表展示元素之前的逻辑关系,通常我们将一个二叉树的结点定义为三个域,分别为左右指针域和数据域。左右指针分别用来给出左孩子和右孩子所在的结点的存储地址。
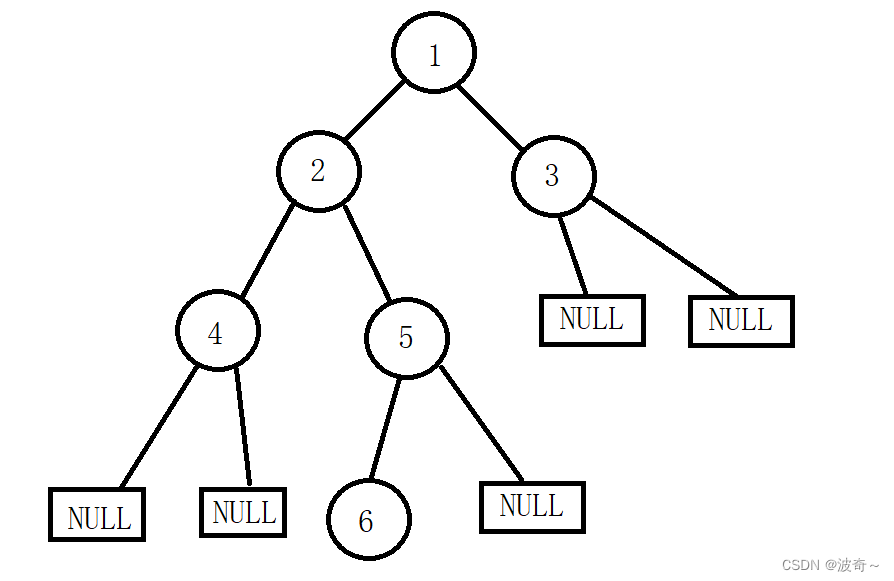
下图便是二叉树的基本表示理论逻辑图,其数据的存储没有特殊的要求,左右孩子可有可无,但是唯独有一个要求就是各个结点的链接不能够交叉,成环等等打断唯一路径的操作。
链式二叉树不同于顺序二叉树,它不需要是完全二叉树,如上图表示一样,它无论在哪一个结点都能指向空。
二叉树的结构代码表示:
typedef int BElementType;
typedef struct BTNode
{
BElementType val;
struct BTNode* LeftChild;
struct BTNode* RightChild;
}BTNode;2、二叉树的遍历
二叉树的遍历除了层序遍历都利用到了递归思想,所以学习这一部分请带上栈争思想。
我们知道,每一次调用函数,操作系统会为我们开辟一片额外的空间用于完成函数功能,并且暂时中断原函数的进程,直到调用的函数结束,才会继续原函数的进程。整个过程就是压栈和出栈操作。
下图中只解释了部分函数递归的操作,不过并不影响我们理解递归,当我们在函数当中调用了自己,在保证程序没有错的情况下,递归结束之后,返回的位置是在调用位置,而不是直接结束了所有函数,这一点很重要。
前中后序遍历:
定义:
前序遍历表示二叉树对结点的访问顺序为根节点、左节点、右节点;
中序遍历表示访问结点的顺序为左节点、根节点、右节点;
后续遍历表示访问结点的顺序为左节点、右节点、根节点。
讲解:
前中后序访问没有本质的区别,只是决定在什么时候读取根的值而已,我这里就用前序遍历作为讲解。我们知道,如果一片地址表示为空证明我们不能在对其做其他的操作,而这在二叉树中表示了我们已经走到了叶子节点,叶子节点没有孩子,表示为空,所以输出为空,返回。
当进入函数的结点不为空,直接对节点的数据域进行访问,然后访问它的左孩子,再访问它的右孩子。注意每次调用该函数,传入的孩子参数在下一个函数里面都表示一个新的根节点,它也有左孩子和右孩子,由此不断地重复。这就是递归所作的划分子问题操作。
代码:
//前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->val);
BinaryTreePrevOrder(root->LeftChild);
BinaryTreePrevOrder(root->RightChild);
}//中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
BinaryTreeInOrder(root->LeftChild);
printf("%d ", root->val);
BinaryTreeInOrder(root->RightChild);
}
//后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
BinaryTreePostOrder(root->LeftChild);
BinaryTreePostOrder(root->RightChild);
printf("%d ", root->val);
}层序遍历:
定义:
层序遍历不同于前三种遍历方式,它是依靠队列这一数据结构实现对二叉树的每一层访问。
讲解:
对于队列我这里不会讲解,如果有兴趣或者是不了解请看我之前的一篇博客,里面有对队列清晰的讲解。
为什么层序遍历需要用到队列呢?很多小伙伴或有这样的疑问,其实利用队列是因为我看上了它先进先出的特点,它能够在上一层的结点出列之后带进它的两个孩子结点进入队列。所以队列的数据域存储的数据为二叉树结点。
由上图可以看到,1先入列,在出列的同时,将2和3带进了队列,在2出列的时候,带进了4结点,还有一个空结点不进入队列。
代码:
//层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
//当root为空树直接返回,没有值
if (root == NULL)
{
printf("树为空");
return;
}
//构建一个队列,将根节点入列
Queue que;
QueueInit(&que);
QueuePush(&que, root);
//当队列还没有为空,继续找结点
while (!QueueEmpty(&que))
{
//保留当前根节点的位置
BTNode* Node = QueueFront(&que);
//输出
printf("%d ", Node->val);
//出列该节点
QueuePop(&que);
//出列之后入列该节点的两个孩子
if (Node->LeftChild)
{
//入左孩子
QueuePush(&que, Node->LeftChild);
}
if (Node->RightChild)
{
//入右孩子
QueuePush(&que, Node->RightChild);
}
}
}4种遍历的访问结果:
3、而二叉树的各个对外操作接口
我们作为函数的创建者知道二叉树的结构等,如果需要将整个程序用于对接其他人,那么就需要提供接口函数用于他人使用,比如求取二叉树结点的个数,求叶子节点个数,找第几层有几个结点,寻找值为x的结点,还有给定一个数组,让我们创建成为二叉树等。
二叉树结点个数:
同样的,该函数的实现使用了递归的方式,我这里就不深入递归了,我们将左边结点的个数保存起来,再把右边结点的个数保存起来,加上根节点的值就等于总的个数了。这里的实现思想为,将一个左孩子递归,让左孩子成为新的根,将右孩子递归,右孩子成为新的根,最终得到的值会返回到Left和Right两个当中。
//结点个数
int BinaryTreeSize(BTNode* root)
{
//遇到空结点,返回0
if (root == NULL)
{
return 0;
}
int Left = BinaryTreeSize(root->LeftChild);
int Right = BinaryTreeSize(root->RightChild);
//返回本结点加上孩子的结点个数
return Left + Right +1;
}二叉树叶子结点个数:
求取叶子节点个数只需要知道,什么是叶子结点,叶子节点即为两个孩子都为空,所以添加一个左右孩子都为空的判断,就能够反应是否找到。找到了就返回1,根据函数调用回归,会返回到Left或者是Right当中,最后将两个变量相加即可。
//查找叶子结点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->LeftChild == NULL && root->RightChild == NULL)
{
return 1;
}
int Left = BinaryTreeLeafSize(root->LeftChild);
int Right = BinaryTreeLeafSize(root->RightChild);
return Left + Right;
}二叉树第k层结点个数:
寻找第k层结点我这里在函数调用参数当中添加了k表示层数,这里的层数其实可以理解为相对层数,第三层对于第一层来说,差距为2,但是相对于第二层来说,差距就为1了,那么我们在使用递归的时候,当k等于1,表示找到了该层,直接返回这个结点,也就是1,若还没有找到,就继续访问它的左孩子和右孩子,并将层数减1,记住减一而不是减减,减减之后会导致整个递归k值错误,程序跑飞的情况。
//找二叉树第k层结点个数
int BinaryTreeLevelSize(BTNode* root, int k)
{
//遇到空结点,返回0
if (root == NULL)
{
return 0;
}
//当走到了目标层数,直接返回结点,打断递归
if (k == 1)
{
return 1;
}
//没到目标层数,往下找
int Left = BinaryTreeLevelSize(root->LeftChild, k - 1);
int Right = BinaryTreeLevelSize(root->RightChild, k - 1);
return Left + Right;
}寻找值为打他的结点:
//查找二叉树中值为data的结点,前序访问
BTNode* BinaryTreeFind(BTNode* root, BElementType data)
{
if (!root)
{
return NULL;
}
//如果结点为目标结点,返回地址
if (root->val == data)
{
return root;
}
//不为当前结点左右孩子都需要查找
BTNode* Left = BinaryTreeFind(root->LeftChild, data);
BTNode* Right = BinaryTreeFind(root->RightChild, data);
//默认左孩子优先
if (Left) return Left;
if (Right) return Right;
return NULL;
}二叉树的前序创建:
这里是通过字符表示的数据,整体思路相信你们也能看懂,我这里就提一下,函数的参数i一定记住要用指针,否则操作加减都对原函数没有关联,会导致函数卡死的情况。
BTNode* Create_BinartTree(char* arr, int* i)
{
if (arr[*i] == '#')
{
(*i)++;
return NULL;
}
struct BTNode* root = (struct BTNode*)malloc(sizeof(struct BTNode));
if (!root)
{
perror("malloc fail");
exit(-1);
}
root->val = arr[(*i)++];
root->LeftChild = Create_BinartTree(arr, i);
root->RightChild = Create_BinartTree(arr, i);
return root;
}销毁二叉树:
销毁只能是后序,因为前序和中序销毁了之后,会找不到其它结点,造成内存泄漏的问题。
//销毁
void BinaryTreeDestroy(BTNode* root)
{
if (root == NULL)
{
return;
}
//利用后序思想,当左右结点都变为空的时候,才到根节点删除
BinaryTreeDestroy(root->LeftChild);
BinaryTreeDestroy(root->RightChild);
free(root);
}
以上就是就是二叉树全部内容哒,希望对你们友帮助咯。