大疆算法笔试题目解析（三）导航

---

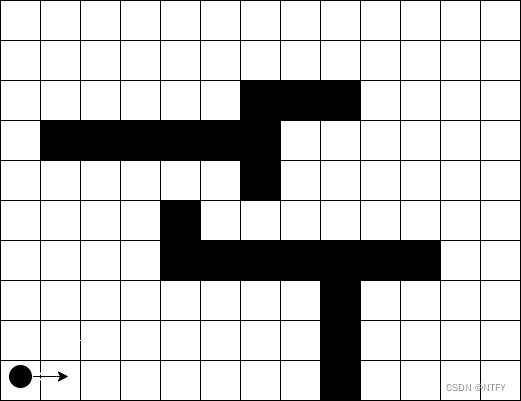
1.（20分）（静态路径规划）考虑一个二维平面静态路径规划问题。以网格形式给定一副全局地图，用$m\times n$的矩阵$M$表示，其中$M(i,j)=1$表示$(i,j)$网格有障碍物，$M(i,j)=0$表示该网格为自由空间。机器人被抽象为一个质点，只可前向运动、转弯，不能侧移、后退，可以在网格中的任意一格向其8个相邻网格运动，不能超越边界。
考虑机器人转向时的代价。假设机器人不转向行驶一个网格消耗能量为1，转向45度消耗能量为0.25（如果转向45度再行驶一个网格消耗能量则为1.25），转向90度的能量为0.5，以此内推。定义网格左下角为坐标原点。
试写出从$S=(0,0)$位置到平面中任一位置$E=(p,q)$的最优路径规划C/C++算法，给出必要说明解释，并分析时间复杂度。
算法输入：矩阵$M,$起始点$S=(0,0),$终点$E=(p,q),$初始运动方向为水平向右。
算法输出：$S$到$E$的最短路径。
数据结构：（可根据算法需要进行更改，包括增加或减少成员变量、成员函数）：

typedef struct _Rect
{//网格定义
	float ang; //父节点到本节点的运动方向，弧度，0为水平向右
	int x;
	int y;
}Rect;

函数声明：void findPath(Rect S, Rect E, bool* M, Rect* path, int m, int n);

---

#include 
#include 
#include 
#include 

#define INF 1e9

struct Rect {
    float ang;
    int x;
    int y;

    Rect(float a, int i, int j) : ang(a), x(i), y(j) {}
};

struct CompareRect {
    bool operator()(const Rect& r1, const Rect& r2) {
        return r1.ang > r2.ang; // 用于优先队列排序
    }
};

float energyCost(float ang) {
    if (ang == 0) return 1;
    if (ang == M_PI / 4 || ang == -M_PI / 4) return 0.25;
    if (ang == M_PI / 2 || ang == -M_PI / 2) return 0.5;
    return 1.25;
}

void findPath(const Rect& S, const Rect& E, const std::vector<std::vector<bool>>& M,
             std::vector<std::vector<float>>& dp, std::vector<std::vector<Rect>>& parent) {
    // 实现路径规划的代码
    // 使用优先队列进行搜索，更新 dp 和 parent 数组
}

std::vector<Rect> reconstructPath(const Rect& S, const Rect& E, const std::vector<std::vector<Rect>>& parent) {
    // 重建最优路径的代码
    // 根据 parent 数组从终点逆向搜索，得到最优路径的 Rect 序列
}

int main() {
    int m, n, p, q;
    std::cin >> m >> n >> p >> q;

    std::vector<std::vector<bool>> M(m, std::vector<bool>(n, false));
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) {
            int val;
            std::cin >> val;
            M[i][j] = (val == 1);
        }
    }

    Rect S(0, 0, 0);
    Rect E(0, p, q);

    std::vector<std::vector<float>> dp(m, std::vector<float>(n, INF));
    dp[S.x][S.y] = 0;

    std::vector<std::vector<Rect>> parent(m, std::vector<Rect>(n, Rect(0, -1, -1)));

    findPath(S, E, M, dp, parent);

    std::vector<Rect> path = reconstructPath(S, E, parent);

    // 输出最优路径
    for (const Rect& point : path) {
        std::cout << "(" << point.x << ", " << point.y << ") ";
    }

    return 0;
}

在这个问题中，我们使用了Dijkstra算法的变种来进行路径规划。Dijkstra算法的时间复杂度取决于使用的数据结构，通常为O((V + E) * log(V))，其中V是顶点数，E是边数。在这里，V为矩阵中的网格数（m * n），E可以近似地认为是每个网格与其相邻的网格数的总和，即8 * m * n。

因此，总的时间复杂度大致为O((m * n + 8 * m * n) * log(m * n))，即O(m * n * log(m * n))。

---

2.（40分）（动态路径规划）考虑封闭2D平面空间内移动机器人的寻路问题。已知地图中标明了起点和目标点，但没有包含障碍物信息。机器人需要依靠传感器（包括摄像头、超声波雷达、激光雷达、惯导单元、陀螺仪等）进行环境感知，且感知范围有限，不足以覆盖整个空间，只能“边走边看”。同时机器人的自身定位需要借助传感器信息进行推算，而传感器信息是基于机器人体坐标系（body,用上标$B$表示)，要考虑全局坐标（global，用上标$G$表示）与体坐标系的转换。
1）（15）某时刻机器人在全局地图中姿态为$(x_0,y_0,\theta {)}^G,$得到一组激光雷达检测到的障碍物坐标数据$\{(x_1,y_1{)}^B,(x_2,y_2{)}^B,...,(x_n,y_n{)}^B\},$求这组障碍物在全局地图中的坐标；
2）（25）设计一个动态路径规划算法，可以根据实时感知信息调整路径。给出算法流程和必要的说明注释。

---

1）首先，我们需要将传感器感知到的障碍物坐标从机器人体坐标系转换到全局坐标系。假设机器人在全局地图中的姿态为$(x_0,y_0,\theta {)}^G$，则障碍物在全局地图中的坐标$(x_i^G,y_i^G)$可以通过以下变换得到：

[ x i G y i G 1 ] = [ cos ⁡ ( θ ) − sin ⁡ ( θ ) x 0 sin ⁡ ( θ ) cos ⁡ ( θ ) y 0 0 0 1 ] [ x i B y i B 1 ] \hspace{66pt}\begin{bmatrix} x_i^G \\ y_i^G \\ 1 \end{bmatrix}= \begin{bmatrix} \cos(\theta) & -\sin(\theta) & x_0 \\ \sin(\theta) & \cos(\theta) & y_0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_i^B \\ y_i^B \\ 1 \end{bmatrix} ​xiG​yiG​1​ ​= ​cos(θ)sin(θ)0​−sin(θ)cos(θ)0​x0​y0​1​ ​ ​xiB​yiB​1​ ​
其中，$(x_i^B,y_i^B)$是传感器感知到的障碍物在机器人体坐标系中的坐标。

2）设计动态路径规划算法的流程如下：

#include 
#include 

struct Obstacle {
    float x;  // 障碍物在机器人体坐标系下的x坐标
    float y;  // 障碍物在机器人体坐标系下的y坐标
};

struct Point {
    float x;  // 全局坐标系中的x坐标
    float y;  // 全局坐标系中的y坐标
};

// 将障碍物坐标从机器人体坐标系转换到全局坐标系
Point transformObstacle(const Point& robotPose, const Obstacle& obstacle) {
    Point globalObstacle;
    globalObstacle.x = robotPose.x + obstacle.x * cos(robotPose.theta) - obstacle.y * sin(robotPose.theta);
    globalObstacle.y = robotPose.y + obstacle.x * sin(robotPose.theta) + obstacle.y * cos(robotPose.theta);
    return globalObstacle;
}

// 动态路径规划算法
std::vector<Point> dynamicPathPlanning(const Point& start, const Point& goal, const std::vector<Obstacle>& obstacles) {
    // TODO: 在这里实现你的动态路径规划算法
    // 可以考虑使用A*算法或其他适合的方法
    
    // 返回一个规划好的路径，表示为一系列全局坐标点
    std::vector<Point> plannedPath;
    return plannedPath;
}

int main() {
    Point robotPose = {x_0, y_0, theta};  // 机器人当前在全局坐标系中的姿态
    std::vector<Obstacle> sensedObstacles = {...};  // 机器人在体坐标系中感知到的障碍物列表
    Point goal = {goal_x, goal_y};  // 全局坐标系中的目标点
    
    // 将感知到的障碍物坐标转换到全局坐标系
    std::vector<Point> globalObstacles;
    for (const Obstacle& obstacle : sensedObstacles) {
        Point globalObstacle = transformObstacle(robotPose, obstacle);
        globalObstacles.push_back(globalObstacle);
    }
    
    // 调用动态路径规划算法
    std::vector<Point> plannedPath = dynamicPathPlanning(robotPose, goal, globalObstacles);
    
    // TODO: 执行规划好的路径，控制机器人运动
    
    return 0;
}

说明：

• transformObstacle函数将机器人体坐标系中的障碍物坐标转换为全局坐标系中的坐标。
• dynamicPathPlanning函数是动态路径规划的核心部分，可以使用A*算法或其他适当的方法来实现。它应该返回一个规划好的路径，表示为一系列全局坐标点。

---

3.（20分）（坐标系变换）考虑大地经纬高度坐标系（也叫GPS坐标系）$(L,B,H),$其中$L$为经度，$B$为纬度，$H$为高度；地心空间直角坐标系$(X,Y,Z),$如下图所示，地球参考椭球长半轴为$a,$短半轴为$b,$已知卯酉圈曲率半径公式为：
$$N=\frac{a}{\sqrt{1-e^{2}si{n}^{2}B}}$$其中$e^2=\frac{a^2-b^2}{a^2}$为第一偏心率。
（1）（10分）写出GPS坐标$(L,B,H)$与直角坐标$(X,Y,Z)$之间的转换关系式。（提示：①GPS高度坐标$H$是距地面高度而非距地心高度；②地球是南北极较扁的椭球体，要用椭球坐标计算而非球体坐标）
（2）（10分）已知某点GPS坐标$(L_0,B_0,H_0),$以该点为原点建立东北天坐标系（站心直角坐标系)；通过坐标原点且指向天顶的法线为z轴（指向天顶为正），以子午线方向为$y$轴（向北为正），$x$轴指向东，且与$y,z$轴垂直（向东为。画出东北天坐标系示意图，标明方向，并推到出另外GPS一点$(L_1,B_1,H_1)$对应东北天坐标$(y,x,z)$的表达式,给出推导过程。（提示：先将GPS坐标转换到直角坐标系，再转换到东北天坐标系）

---

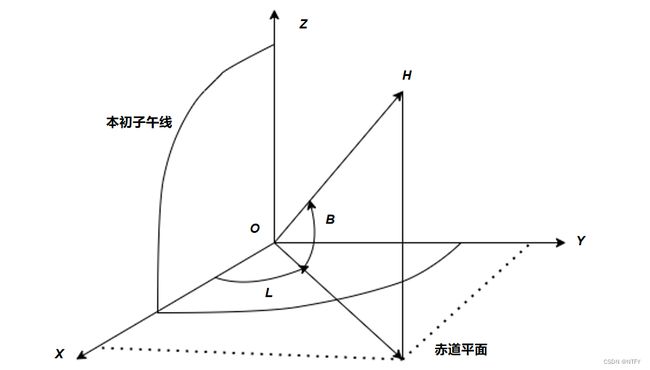
（1）GPS坐标$(L,B,H)$与地心直角坐标$(X,Y,Z)$之间的转换关系式如下：

$$\begin{array}{rl}X& =(N+H)\cos B\cos L\\ Y& =(N+H)\cos B\sin L\\ Z& =\left(\frac{b^2}{a^2}N+H\right)\sin B\end{array}$$

其中，$N$为卯酉圈曲率半径。

（2）东北天坐标系示意图如下：

       Y
       |
       |
       o -- X
      /
     /
    Z

其中，$X$轴指向东，$Y$轴指向北，$Z$轴指向天顶。现在来推导GPS点$(L_1,B_1,H_1)$对应的东北天坐标$(y,x,z)$表达式：

首先，将GPS坐标$(L_1,B_1,H_1)$转换为地心直角坐标$(X_1,Y_1,Z_1)$，使用之前的转换关系式：

$$\begin{array}{rl}{X}_1& =(N+H_1)\cos B_1\cos L_1\\ Y_1& =(N+H_1)\cos B_1\sin L_1\\ Z_1& =\left(\frac{b^2}{a^2}N+H_1\right)\sin B_1\end{array}$$

然后，将地心直角坐标$(X_1,Y_1,Z_1)$转换为东北天坐标$(y,x,z)$：

$$\begin{array}{rl}x& =-Y_1\sin L_0+X_1\cos L_0\\ y& =Y_1\cos L_0+X_1\sin L_0\\ z& =Z_1\cos B_0-X_1\cos L_0\sin B_0-Y_1\sin L_0\sin B_0\end{array}$$

其中，$(L_0,B_0)$为原点$(L_0,B_0,H_0)$所对应的经度和纬度。

这样就得到了GPS点$(L_1,B_1,H_1)$对应的东北天坐标$(y,x,z)$的表达式。

---

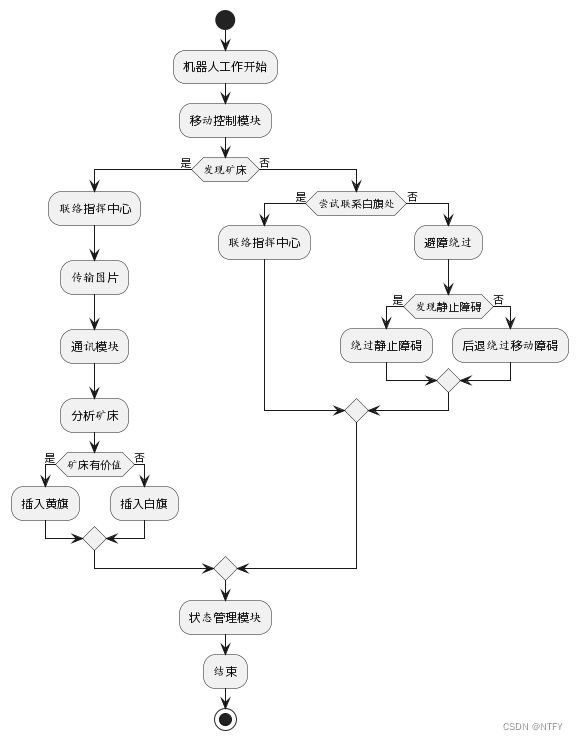
4、(20分)从下面一段文字提炼机器人的工作逻错，总结出其对应的系统模型、UML图、状态机或者任何可以帮助机器人编程开发的框图
机器人在空间中移动，寻找矿藏。如果它发现了可能的矿床，就会联络指挥中心，传回图片到指挥中心分析矿床。指挥中心将分析结果反馈给机器人，如果是有价值的矿产就插一面黄旗在矿床旁边，否则就插一面红旗。如果机器人在矿床旁边三次尝试都没法联络到指挥中心，就插下一面白旗。机器人可以重新返回一个插有白旗的位置，重新尝试联络。机器人活动的过程中不能把之前插下的旗子碰倒。
机器人在移动的过程中如果发现静止的障碍，就会尝试从无障碍的方向绕过。如果发现移动的障碍，则会直接后退。
机器人可以通过GPS知道自己的位置，还可以通过避障系统知道障碍与自己的相对位置。
连接通畅时，任何时候指挥中心发出紧急控制指令都可以中断机器人的自主行动，紧急控制指令也可以取消，让机器人回复自主行动。

---

这段文字描述了机器人在空间中寻找矿藏并进行相关操作的工作流程。可以总结出以下内容：

系统模型：

该系统可以建模为一个多模块的机器人控制系统，包括以下模块：

1. 移动控制模块：负责机器人在空间中的移动和避障。
2. 通讯模块：负责机器人与指挥中心的通信，传输图片和分析结果。
3. 图像分析模块：负责分析矿床图片，判断是否有价值的矿产。
4. 标识模块：负责在矿床旁边插入旗子，根据矿床价值插入黄旗或白旗。
5. 状态管理模块：管理机器人的状态变化和状态转换。

UML图：

以下是一个简化的UML活动图，展示了机器人的工作流程和各个模块之间的交互：

---