Python——快速傅里叶变换

1.题目 

      给出时域函数,对其采样获得采样数据，并画出对应的x-t曲线；然后对上述采样数据进行傅里叶变换，画出频谱图。运行该程序，需要从键盘输入N中的r值，该程序可以接受的值为5-10的整数。

---

2.算法及分析

   一般地来说，若具有N个采样点，第L层节点的值为：

    在处理该问题的时候，我们要确定的指数值。对于节点,其p值的可以按照下列方式确定。首先将n用r位二进制形式表示出来，再将改二进制右移r-l位，左边空位补零；然后在将码序倒置，最后再将改二进制写出十进制形式，就确定p值。

    而上式中涉及的两个点为对偶节点。在程序上实现的时候注意对偶节点。

---

3.程序

import numpy as np
import math as ma
import cmath
import matplotlib.pyplot as plt
def f(t,N):
    x=ma.cos(2*ma.pi/N*t)+0.5*ma.cos(2*2*ma.pi/N*t)+0.8*ma.cos(5*2*ma.pi/N*t)
    return x
r=int(input('输入（5-10）整数'));N=2**r;n=N/2;c=0;nu=0;
t=np.arange(0,N,1);y=np.zeros((N,r));p=np.zeros((N,r))
x=np.zeros((N,1));x1=[]
for i in range(N):
    m=list(bin(i))
    for j in range(len(m)-2):
        y[i,r-1-j]=float(m[len(m)-j-1])
for l in range(1,r+1):
    z=np.zeros((N,r))
    for no in range(r):
        if r-no-1-(r-l)>=0:
            z[:,r-no-1]=y[:,r-no-1-(r-l)]
    for nk in range(N):
        c=0
        for mk in range(r):
            c=c+z[nk,mk]*2**mk
        p[nk,l-1]=c
for nk in range(N):
    x[nk,0]=f(nk,N)
x=x+0j
for j in range(N):
    x1.append(j)
y1=np.array([x1]);
for io in range(1,r+1):
    y1=y1.reshape((2**io,-1))
    b=int(y1.shape[0]/2);l=y1.shape[1];lp=0
    mn=np.zeros((2,int(N/2)))
    for nk in range(l):
        for nl in range(b):
            bg=2*(nl+1)-1
            bv=2*(nl+1)-2
            mn[0,lp]=y1[bv,nk]
            mn[1,lp]=y1[bg,nk]
            lp=lp+1
    a1=np.lexsort(mn[::-1,:])
    mn=mn[:,a1]
    a2=np.lexsort(mn[0:2,:])
    mn=mn[:,a2];nk1=np.zeros((N,1));
    for lop in range(int(N)):
         nk1[lop,0]=x[lop,0]
    for nk in range(int(N/2)):
         pg=[]
         for gg in mn[:,nk]:
            pg.append(gg)
         x[int(pg[0]),0]=nk1[int(pg[0]),0]+cmath.exp(-2*ma.pi*1j/int(N)*p[int(pg[0]),io-1])*nk1[int(pg[1]),0]
         x[int(pg[1]),0]=nk1[int(pg[0]),0]+cmath.exp(-2*ma.pi*1j/int(N)*p[int(pg[1]),io-1])*nk1[int(pg[1]),0]
x=abs(x)
bf=x.reshape(1,-1)
x=np.arange(0,N,1)
x=np.array([x])
y=[];m=0
zk=np.zeros((1,int(N)))
for ba in p[:,-1]:
    zk[0,int(ba)]=bf[0,m]
    m=m+1
for bb in zk:
    for bh in bb:
        y.append(bh)
        for nm in range(100):
            y.append(0)
vf=[]
for nn in x:
    for vvc in nn:
        vf.append(vvc)
        for llk in range(100):
            vf.append(vvc+llk*0.01)
plt.plot(vf,y)
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.xlabel('K值')
plt.ylabel('频谱幅度')
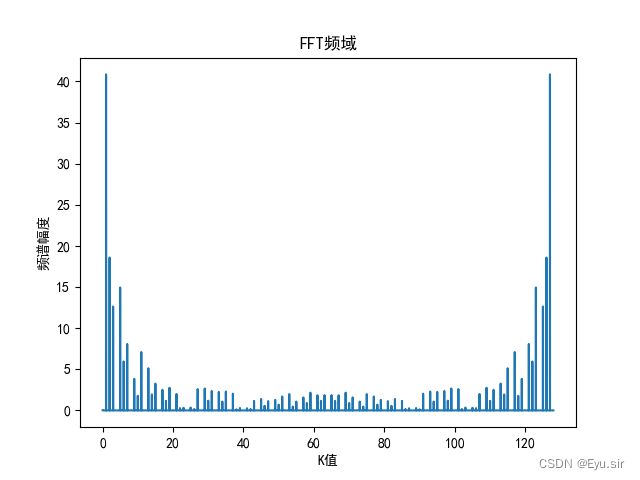
plt.title('FFT频域')
plt.show()
mk=[];po=[]
for bg in range(int(N)+1):
    mk.append(f(bg,N))
    po.append(bg)
mk1=[];pno=[]
for bg2 in range(0,int(N)*25):
    mk1.append(f(bg2,N))
    pno.append(bg2)
plt.plot(pno,mk1)
plt.scatter(po,mk)
plt.ylabel('x')
plt.xlabel('t')
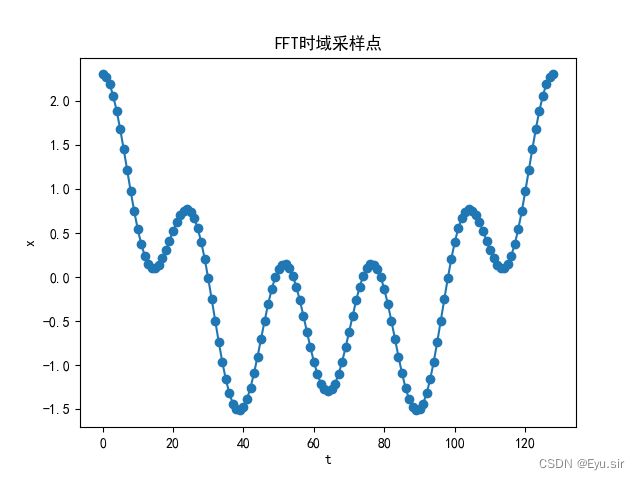
plt.title('FFT时域')
plt.show()
plt.scatter(po,mk)
plt.plot(po,mk)
plt.ylabel('x')
plt.xlabel('t')
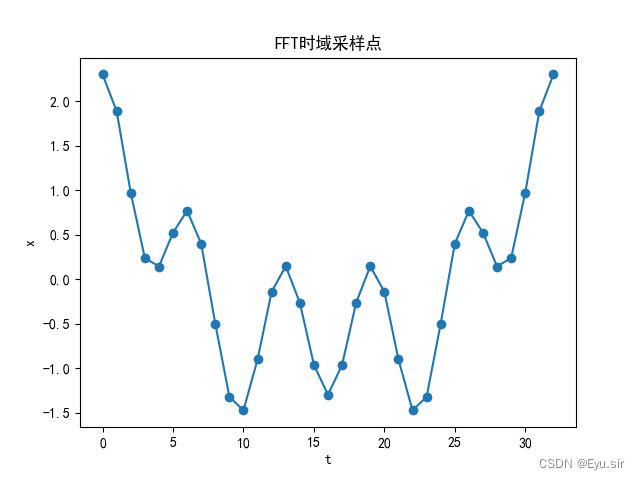
plt.title('FFT时域采样点')
plt.show()

---

4.结果

（1）r=5

---

（2）r=7

---

5.实验总结

    （1）从程序的结果来看，我们可以用有限的频谱空间来表征比较复杂的时域空间，可以将问题大大的简化；

    （2）本次程序使用的方法为FFT方法，它的优势很明显，就是快速。从多次的乘法和加法变为几次的乘法和简单的加减法，可以大大的减少计算量；

    （3）本次程序的编程难点：1.确定p的值2.确定对偶节点；本次程序较为优势的时候，可以输出所有P点以及每层的对偶节点。相对来说更容易展示程序的正确性。