机器学习: 简单讲极大似然估计和贝叶斯估计、最大后验估计

一、前言

我在概率论：参数估计里面提到了极大似然估计，不熟悉的可以看一下，本文重点介绍后两者估计方法。

在这里两种估计方法估计的是什么？我们使用一个较为泛化的问题表示：

考虑这样一个问题：总体X的概率密度函数为$p(x|\theta )$，但该密度函数未知，我们只观测到一组样本$\left(x_1,x_2,\dots ,x_n\right)$ ，我们需要估计的是参数$\theta$，且最终目的都是根据$\theta$给出总体X的概率密度函数$p(x|\theta )$。

下面我们将采用不同的估计方法来求解这个问题，并将说明三种估计方法的区别和联系。

二、极大似然估计

1. 极大似然估计的过程

在进行贝叶斯分类的时候，通常需要知道$P(w_i),P(x|w_i)$的值，在这里$w_i$表示第i类。但是与$P(x|w_i)$所相关的分布所包含的参数通常是未知的（比如说假设$P(x|w_i)$服从正态分布，那么它的均值和方差通常是未知的。

为了简化问题，我们认为$P(x|w_i)\sim N(u_i,{\Sigma }_i)$（即服从正态分布，一般都这样干）:。此时我们想知道概率$P(x|w_i)$，就需要根据已有的样本估计 $u_i,{\Sigma }_i$

根据上述的问题简化，我们有
$$\begin{array}{rl}& p\left(x\mid {\omega }_j\right)\sim N\left({\mu }_j,{\Sigma }_j\right)\\ & p\left(x\mid {\omega }_j\right)\equiv p\left(x\mid {\omega }_j,{\theta }_j\right)\end{array}$$
其中，
$${\theta }_j=\left({\mu }_j,{\Sigma }_j\right)=\left({\mu }_j^1,{\mu }_j^2,\dots ,{\sigma }_j^1,{\sigma }_j^2\dots \right)$$
给定训练样本$D=（x_1，x_2，\dots ，x_n）$如何估计$\theta$？

极大似然估计的一个思想就是“存在即合理”。就是样本既然存在了，那么我认为在它所服从的分布中，它的出现的可能性是最大的（这就是极大似然）

接下来就求所有数据出现的一个联合概率。

$$p(D\mid \theta )=\prod _{k=1}^{k=n}p\left(x_k\mid w,\theta \right)=\prod _{k=1}^{k=n}p\left(x_k\mid \theta \right)=F(\theta )$$
$p(D\mid \theta )$ is called the likelihood of $\theta$

此时我们把这个联合概率看作$\theta$的函数（似然函数），那么当该函数取得最大值时的$\hat{\theta }$，是$\theta$真实值的一个合理估计。举例说明：

2. 极大似然估计的优缺点

1. 优点
   具有良好的收敛性，即使样本量增加
   比任何其他替代技术都更简单，因此计算复杂度更低。
2. 缺点
   极大似然估计的参数只拟合观测到的样本，如果观测到的样本并不能很好的代表总体样本的分布，那么极大似然估计是不准确的。

三、贝叶斯估计

在极大似然估计中，它认为参数是固定的，但未知！固定就是指它只有一个值。

但是贝叶斯估计将参数视为具有某些已知先验分布的随机变量。也就是说$\theta$本身也服从一个分布。这样其实是可以避免参数只拟合观测到的样本的，因为我们假设参数$\theta$本身也服从一个分布，不是由观测样本完全决定的。

1. 浅谈$p(x)和p(x|\theta )$的关系

给定一个随机变量X，现在经过抽样，我们得到一组样本$D=\left(x_1,x_2,\dots ,x_n\right)$, 我们希望通过观察到的这组样本知道X的一个具体分布，该分布的概率密度函数为p(x)，因为借此我们可以得知一个具体的样本，它出现的概率是多少。

所以一切的目标是想要得到p(x)。但是只有一组样本，我们甚至连p(x)是关于什么的函数都不知道。

于是我们进一步做出合理的假设（称为条件），设p(x)的参数是$\theta$，但它未知。

这还不够，我并不知道这个概率密度函数是个什么形式，我们还需要进行假设。一般我们会假设它是正态分布（当然也可以是其他分布），这就是我们说的服从什么什么分布。

所以可以知道p(x)是x的一个关于某个分布的概率密度函数(没法根据样本求出）。

$p(x|\theta )$是设定了参数$\theta$, 且设定了是关于某种分布的概率密度函数（可以根据假设和给定样本求出）。

所以不同的符号表示其实都是表示关于x的概率密度函数，符号$p(x|\theta )$表示给出的关于x的概率密度函数是基于某两个条件的。

2. $\theta$本身也服从一个分布，如何给出x的概率密度函数$p(x)$

此时一种思路就是遍历变量$\theta$的每一种可能取值，然后求$p(x|\theta )$的平均，作为关于x的概率密度函数。也就是：

$$\int p(\mathbf{x}\mid \mathbf{\theta })p(\mathbf{\theta }\mid \mathcal{D})d\mathbf{\theta }$$

这里我们认为$\theta$的分布应当从训练样本D中得到，所以使用了后验条件分布的概率密度函数$p(\mathbf{\theta }\mid \mathcal{D})$。

另外，这样得到的关于x的概率密度函数的信息其实最开始是从D中得到的，为了做区别，我们认为这个关于x的概率密度函数应当用一个后验分布的新符号表示，即

$$p(\mathbf{x}\mid \mathcal{D})=\int p(\mathbf{x}\mid \mathbf{\theta })p(\mathbf{\theta }\mid \mathcal{D})d\mathbf{\theta }$$

值得注意的是当变量$\theta$取定某一个值时，跟本节1.讨论的结果一样，也是假设$p(x|\theta )$的分布形式是已知的（人为选定的，如是参数为$\theta$的正态分布）。

因此，现在需要求的就是$p(\mathbf{\theta }\mid \mathcal{D})$。直接求没法求，这里用到了贝叶斯公式（或许这就是称为贝叶斯估计的原因）。

$$\begin{array}{rl}p(\theta \mid \mathcal{D})& =\frac{p(\mathcal{D}\mid \theta )p(\theta )}{\int p(\mathcal{D}\mid \theta )p(\theta )d\theta }\\ & =\alpha \prod _{k=1}^{n}p\left(x_k\mid \theta \right)p(\theta )\end{array}$$

根据上面的讨论可知，$p\left(x_k\mid \theta \right)$的分布形式是已知的，因此它的值是可求的。这里的$p(\theta )$又是什么呢？根据贝叶斯公式我们需要这个值才能计算，因此我们又需要再次假设一个$\theta$的原始分布，它的概率密度函数是$p(\theta )$。这个分布的形式和参数是人为选定的，常见的如均匀分布，正态分布等。

下面我们从一个例子再次阐述上面的过程。

3. 例子：单变量的情况 $\theta =\mu$

现在我们假设
$$p(x\mid \mu )\sim N\left(\mu ,{\sigma }^2\right)(3.1)$$

并且设$\theta$的原始分布为已知值${\mu }_0,{\sigma }_0^2$的正态分布

$$p(\mu )\sim N\left({\mu }_0,{\sigma }_0^2\right)(3.2)$$

此时我们求参数$\mu$的后验分布

$$\begin{array}{rl}p(\mu \mid \mathcal{D})& =\frac{p(\mathcal{D}\mid \mu )p(\mu )}{\int p(\mathcal{D}\mid \mu )p(\mu )d\mu }\\ & =\alpha \prod _{k=1}^{n}p\left(x_k\mid \mu \right)p(\mu )\end{array}(3.3)$$

根据上面的两个分布假设3.1,3.1，我们有
$$\begin{array}{rl}p(\mu \mid \mathcal{D})& =\alpha \prod _{k=1}^n\frac{1}{\sqrt{2\pi }\sigma }\exp \left[-\frac{1}{2}{\left(\frac{x_k-\mu }{\sigma }\right)}^2\right]\frac{1}{\sqrt{2\pi }{\sigma }_0}\exp \left[-\frac{1}{2}{\left(\frac{\mu -{\mu }_0}{{\sigma }_0}\right)}^2\right]\\ & ={\alpha }^{\prime }\exp \left[-\frac{1}{2}\left(\sum _{k=1}^n{\left(\frac{\mu -x_k}{\sigma }\right)}^2+{\left(\frac{\mu -{\mu }_0}{{\sigma }_0}\right)}^2\right)\right]\\ & ={\alpha }^{\prime \prime }\exp [-\frac{1}{2}\left[\left(\frac{n}{{\sigma }^2}+\frac{1}{{\sigma }_0^2}\right){\mu }^2-2\left(\frac{1}{{\sigma }^2}\sum _{k=1}^n{x}_k+\frac{{\mu }_0}{{\sigma }_0^2}\right)\mu \right]\end{array}(3.4)$$

然后我们可以将其化简为正态分布的形式

$$p(\mu \mid \mathcal{D})=\frac{1}{\sqrt{2\pi }{\sigma }_n}\exp \left[-\frac{1}{2}{\left(\frac{\mu -{\mu }_n}{{\sigma }_n}\right)}^2\right](3.5)$$

其中需满足：
$$\begin{array}{c}\frac{1}{{\sigma }_n^2}=\frac{n}{{\sigma }^2}+\frac{1}{{\sigma }_0^2}\\ \frac{{\mu }_n}{{\sigma }_n^2}=\frac{n}{{\sigma }_2}{\bar{x}}_n+\frac{{\mu }_0}{{\sigma }_0^2}\end{array}(3.6)$$

求解上述方程可得
$$\begin{array}{c}{\bar{x}}_n=\frac{1}{n}\sum _{k=1}^n{x}_k\\ {\mu }_n=\left(\frac{n{\sigma }_0^2}{n{\sigma }_0^2+{\sigma }^2}\right){\bar{x}}_n+\frac{{\sigma }^2}{n{\sigma }_0^2+{\sigma }^2}{\mu }_0\\ {\sigma }_n^2=\frac{{\sigma }_0^2{\sigma }^2}{n{\sigma }_0^2+{\sigma }^2}\end{array}(3.7)$$

此时将3.5带入下式求积分可得到最终的关于x的概率密度函数

$$p(\mathbf{x}\mid \mathcal{D})=\int p(\mathbf{x}\mid \mathbf{\mu })p(\mathbf{\mu }\mid \mathcal{D})d\mathbf{\mu }$$

三、极大后验估计（MAP estimators (Max a posteriori)）

极大后验估计可以说是极大似然估计和贝叶斯估计思想的融合。首先它跟贝叶斯估计一样，也假设参数是变量，服从某个已知分布。但是它不会遍历变量$\theta$的每一种可能取值，然后求$p(x|\theta )$的平均。相反，它是取$\theta$的所有值中最有可能的取值$\hat{\theta }$，然后给出$p(x|\hat{\theta })$。那这个最有可能的取值其实就是$p(\mathbf{\theta }\mid \mathcal{D})$取最大值时参数$\theta$的取值$\hat{\theta }$.

$${\hat{\mathbf{\theta }}}_{\text{map }}=\arg \underset{\mathbf{\theta }}{\max }p(\mathbf{\theta }\mid \mathcal{D})=\arg \underset{\mathbf{\theta }}{\max }\frac{p(\mathcal{D}\mid \theta )p(\theta )}{\int p(\mathcal{D}\mid \theta )p(\theta )d\theta }=\arg \underset{\mathbf{\theta }}{\max }p(\mathcal{D}\mid \theta )p(\theta )$$

这里$\int p(\mathcal{D}\mid \theta )p(\theta )d\theta$求完积分后不再是包含$\theta$的函数，因此视为常数忽略掉。

在很多文章里面，最大后验估计是如下这样表达的：

$${\hat{\mathbf{\theta }}}_{\text{map }}=\arg \underset{\mathbf{\theta }}{\max }\pi (\mathbf{\theta }\mid \mathbf{x})=\arg \underset{\mathbf{\theta }}{\max }\frac{f(\mathbf{x}\mid \mathbf{\theta })\pi (\mathbf{\theta })}{m(\mathbf{x})}=\arg \underset{\mathbf{\theta }}{\max }f(\mathbf{x}\mid \mathbf{\theta })\pi (\mathbf{\theta })$$

上面两个式子的$\mathcal{D}$和$\mathbf{x}$意义是一致的，表示观测样本。但本文使用$\mathcal{D}$表示观测样本，用$\mathbf{x}$表示总体样本，所以为了避免混淆，采用第一个公式表达。

四、贝叶斯估计和最大后验估计

当$p(\mathbf{\theta }\mid \mathcal{D})$的函数图像非常的尖锐的时候，贝叶斯估计约等于最大后验估计。

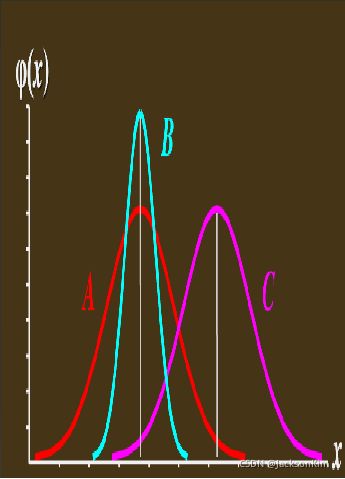
比如图中B曲线十分尖锐，对于即当$\theta =\hat{\theta }$时，概率接近于1.此时
$$p(x\mid D)=\int p(x\mid \theta )p(\theta \mid D)d\theta \cong p(x\mid \hat{\theta })$$

此时贝叶斯估计给出的关于x的概率密度函数非常接近$p(x\mid \hat{\theta })$，最大后验估计给出的关于x的概率密度函数就是$p(x\mid \hat{\theta })$，因此我们说他们此时是近似的。

五、极大似然估计和最大后验估计

在最大后验估计中，如果我们认为$\theta$的先验分布是一个均匀分布，即$p(\theta )$为常数C，那么最大后验估计变为
$$\arg \underset{\mathbf{\theta }}{\max }p(\mathcal{D}\mid \theta )C$$
此时它等价于极大似然估计。

六、频率学派和贝叶斯学派

1.频率学派

他们认为世界是确定的。他们直接为事件本身建模，也就是说事件在多次重复实验中趋于一个稳定的值p，那么这个值就是该事件的概率。

他们认为模型参数是个定值，希望通过类似解方程组的方式从数据中求得该未知数。这就是频率学派使用的参数估计方法-极大似然估计（MLE），这种方法往往在大数据量的情况下可以很好的还原模型的真实情况。

2.贝叶斯学派

他们认为世界是不确定的，因获取的信息不同而异。假设对世界先有一个预先的估计，然后通过获取的信息来不断调整之前的预估计。 他们不试图对事件本身进行建模，而是从旁观者的角度来说。因此对于同一个事件，不同的人掌握的先验不同的话，那么他们所认为的事件状态也会不同。

他们认为模型参数源自某种潜在分布，希望从数据中推知该分布。对于数据的观测方式不同或者假设不同，那么推知的该参数也会因此而存在差异。这就是贝叶斯派视角下用来估计参数的常用方法-最大后验概率估计（MAP），这种方法在先验假设比较靠谱的情况下效果显著，随着数据量的增加，先验假设对于模型参数的主导作用会逐渐削弱，相反真实的数据样例会大大占据有利地位。极端情况下，比如把先验假设去掉，或者假设先验满足均匀分布的话，那她和极大似然估计就如出一辙了。

可见，贝叶斯估计和最大后验估计其实是基于贝叶斯学派的哲学思想发展的参数估计方法。

七、参考资料

1. 《模式分类》Richard O. Duda ，Peter E.Hart ，David G.Stork
2. 极大似然估计和贝叶斯估计
3. 极大似然估计与最大后验概率估计