哈夫曼树与哈夫曼编码实验报告（直接运行）

一.实验目的：

理解二叉树的基本逻辑结构，完成最优二叉树的构建、遍历。

通过对简单哈夫曼编/译码系统的设计与实现来熟练掌握树型结构在实际问题中的应用。

二.实验内容：

题目：哈夫曼编码/译码

问题描述：

利用哈夫曼编码进行通信可以大大提高信道利用率，缩短信息传输时间，降低传输成本。但是，这要求在发送端通过一个编码系统对待传数据预先编码，在接收端将传来的数据进行译码（复原）。对于双工信道（即可以双向传输信息的信道），每端都需要一个完整的编/译码系统。试为这样的u信息收发编写一个哈夫曼码的编/译码系统。

基本要求：

1. 接收原始数据（电文）：从终端输入电文（电文为一个字符串，假设仅由26个小写英文字母构成）。

（2）编码：利用已建好的哈夫曼树，对电文进行编码。

（3）打印编码规则：即字符与编码的一一对应关系。

（4）打印显示电文以及该电文对应的哈夫曼编码。

（5）接收原始数据（哈夫曼编码）：从终端输入一串哈二进制哈夫曼编码（由

0和1构成）。

（6）译码：利用已建好的哈夫曼树对该二进制编码进行译码。

（7）打印译码内容：将译码结果显示在终端上。

三. 实验方案

（一）算法设计思路：

1.遍历电文获取各个字符的权重传递到哈夫曼树

2、建立哈夫曼树：

遍历整体，把两个最小的权重相加，作为新的权重 和剩余的权重重新排列，再把最小的两个权重相加，再重新排列，直到最后变成1。

3、根据哈夫曼树获取哈夫曼编码 打印对应关系

4、利用建立好的哈夫曼树进行解码

（二）使用模块及变量的说明（例如结构体的定义、含义）

1、typedef struct HNodeType        //定义哈夫曼树的叶结点

2、HNodeType HFMTree[2 * n - 1];   //建立存储哈夫曼树的数组

3、void Creat_HuffMTree(HNodeType HFMTree[],int num[])

                                   //建立哈夫曼树

4、typedef struct HCodeType        //定义哈夫曼编码的结点

5、HCodeType HuffCode[n];          //建立存储编码的数组

6、void HaffmanCode(HNodeType HFMTree[], HCodeType HuffCode[]);

                                   //按照左0右1获取哈夫曼编码

    7、int qnum(string str, int num[]);//获取电文中每个字母出现次数

    8、void print(HNodeType HFMTree[], HCodeType HuffCode[], int num[]);

                                       //打印字母出现次数及对应编码

    9、void translate_CI(string str);  //将电文字符串编码并输出

    10、int length(string str);        //获取字符串长度

    11、void decode(HNodeType HFMTree[], HCodeType HuffCode[], string str);                                  //译码，将0-1转为字符串

四. 实验步骤或程序（经调试后正确的源程序）

#include 

#include

using namespace std;

#define n 26         //26个字母

#define MAXVALUE 1000

typedef struct

{

    int weight;

    int parent;

    int lchild;

    int rchild;

   

}HNodeType ;

HNodeType HFMTree[2 * n - 1];

void Creat_HuffMTree(HNodeType HFMTree[],int num[])//叶结点为n=4

{

    int m1, m2, x1, x2;//x1 x2 存放最小和次小权值 m1 m2存放下标

    int i, j;

    for (i = 0; i < 2 * n - 1; i++)

    {

        HFMTree[i].weight = 0;

        HFMTree[i].parent = -1;

        HFMTree[i].rchild = -1;

        HFMTree[i].lchild = -1;



    }

    for (i = 0; i < n; i++)

    {

        //cin >> HFMTree[i].weight;//输入n个叶结点的权重

        HFMTree[i].weight = num[i];

    }

    for (i = 0; i < n-1; i++)

    {

        x1 = x2 = MAXVALUE;

        m1 = m2 = -1;

        for (j = 0; j < n + i; j++)

        {

            if (HFMTree[j].parent == -1 && HFMTree[j].weight < x1)

            {

                x2 = x1; m2 = m1;

                x1 = HFMTree[j].weight; m1 = j;

            }

            else if (HFMTree[j].parent == -1 && HFMTree[j].weight < x2)

            {

                x2 = HFMTree[j].weight; m2 = j;

            }



        }

        HFMTree[m1].parent = n + i; HFMTree[m2].parent = n + i;

        HFMTree[n + i].weight = HFMTree[m1].weight + HFMTree[m2].weight;

        HFMTree[n + i].lchild = m1; HFMTree[n + i].rchild = m2;

    }



}

typedef struct

{

    int bit[n];

    int start;

}HCodeType;

HCodeType HuffCode[n];

void HaffmanCode(HNodeType HFMTree[], HCodeType HuffCode[])

{

    HCodeType cd;

    int i, j, c, p;//p是父母 c是孩子

    for (i = 0; i < n; i++)

    {

        cd.start = n - 1;

        c = i;

        p = HFMTree[c].parent;

        while (p != -1)

        {

            if (HFMTree[p].lchild == c)

            {

                cd.bit[cd.start] = 0;

            }

            else

            {

                cd.bit[cd.start] = 1;

            }

            cd.start--;

            c = p;

            p = HFMTree[c].parent;

        }

        for (j = cd.start + 1; j < n; j++)

            HuffCode[i].bit[j] = cd.bit[j];

        HuffCode[i].start = cd.start + 1;

       



    }

}

int qnum(string str, int num[]);

void print(HNodeType HFMTree[], HCodeType HuffCode[], int num[]);

void translate_CI(string str);

int length(string str);

void decode(HNodeType HFMTree[], HCodeType HuffCode[], string str);

int main()

{

  





    int num[n] = {0};//1.注意初始化

    



    string str,str1;

        cout << "输入电文：";

        cin >> str;

        qnum(str, num);

        Creat_HuffMTree(HFMTree, num);//形成哈夫曼树

        HaffmanCode(HFMTree, HuffCode);

        print(HFMTree, HuffCode, num);

        translate_CI(str);

   

        cout << endl;

        while (1)

        {

            cout << endl<<"输入0—1二进制串(按e退出)：";

            cin >> str1;

            if (str1 == "e")

                break;

            int len = length(str1);

          //  translate_IC(str1, len);

         

            decode(HFMTree, HuffCode, str1);

        }

       

   

    system("pause");

  

    return 0;

}



int length(string str)

{

    int i = 0;

    while (str[i] != '\0')

    {

        i++;

    }



    return i;

}

int qnum(string str,int num[]) //获取每个字母出现次数

{

   

    int j,k;

    for (int i = 0; i < length(str); i++)

    {  

        k = str[i];

       j= (int)k - 97;

       num[j]++;

    }

    return 1;

}

void print(HNodeType HFMTree[], HCodeType HuffCode[], int num[])//输出各个字符出现的次数及对应的编码

{

    int m = 2 * n - 1;

    char ch;

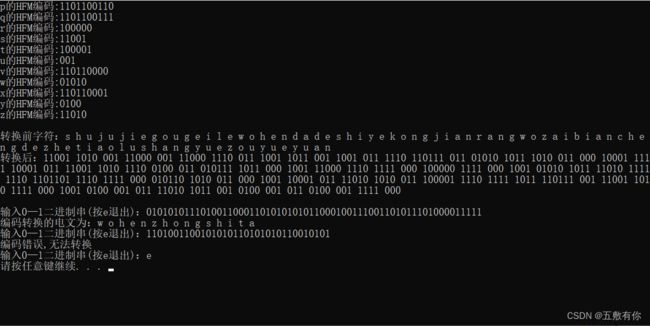
    cout << endl<<"电文中出现的字符及其数字如下："<

五．程序运行结果（程序运行结果的一些截图）

 

 

 

六．实验总结（调试过程中遇到哪些问题，怎么解决的）

问题一：26个字母如何建立好哈夫曼树

      我想了一下就以数组的形式在下标为0-25的空间中依次逻辑对应a-z,因为在建立哈夫曼树时会遍历整体，所以怎么在这26个空间存无所谓只需要逻辑对应就行；

问题二：每个叶节点权重怎么传递

      开辟一个num[25],遍历整个电文，利用ascll码-97就能依次存num[i]中利用HFMTree[i].weight=num[i],完美传递权重.

入

问题三：解码的时候不知道如何截取一截对应

      刚开始想要依靠字符串拼接一次一次的遍历循环找对应，但算法太累，循环次数过多等缺点过于明显放弃。

       之后通过查找CSDN理解原来可以依靠哈夫曼树，只要这个结点左右孩子下标都是-1就是找到了对应的字符，然后存进数组就行，可行性高，逻辑明确。