十大排序图示详解（java代码）
目录
- 前言
-
- 十大算法的分类
- 十大算法简略分析
- 一、冒泡排序
-
- 原理
- 图解
- java代码：
- 二、直接插入排序
-
- 原理
- 图解
- java代码：
- 三、希尔排序
-
- 原理
- 图示
- java代码
- 四、选择排序
-
- 原理
- 图解
- Java代码：
- 五、快速排序
-
- 原理
- 图解
- java代码：
- 六、归并排序
-
- 原理
- 图解
- java代码（二路归并）：
- 七、堆排序
-
- 小顶堆
-
- 原理
- 图解
- java代码（小堆顶）
- 大顶堆
- 八、桶排序
-
- 原理
- 图解
- java代码：
- 九、基数排序
-
- 原理
- 图解
- java代码：
- 十、计数排序
-
- 原理
- 图解
- java代码：
前言
十大算法的分类
- 博主是一个喜欢简略的人，不喜欢那些复杂的概念，所以博主在写原理的时候基本都是一句大白话，简单易懂，相比那些云里雾里的概念，我还是比较喜欢用自己的话来说明
十种常见的排序算法可以分为两大类：
比较排序：在排序的过程中，每个元素都要与其他元素进行比较才能确定自己的位置
非比较排序：不通过比较元素之间的大小来排序
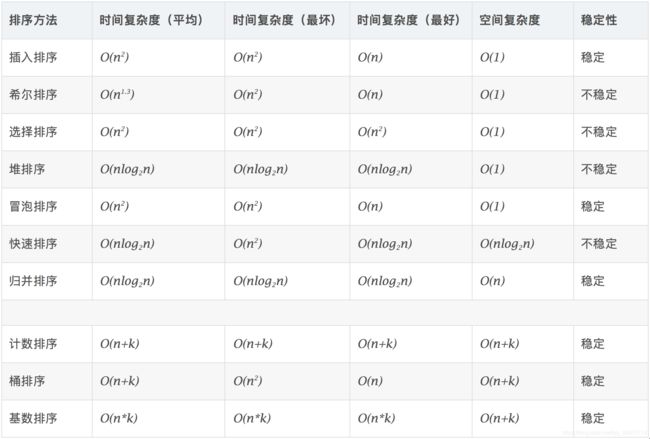
十大算法简略分析
在这里解释一下什么是稳定性：
假设a在b的前面，a = b，排序完成后，a还在b的前面，此为稳定，反正不稳定
还有在这里说明一下，关于时间复杂度这个很重要，许多人只是简单的记住了某些排序的时间复杂度，却不会分析，这其实并没有什么用，我们要知道O(n) ,O(n^2),O(nlogn)是怎么来的
我们简单举个例子
for (int i = 0 ; i < n ; i++) { //1
for(int j = 0 ; j < n ; j++) { //2
num = num + i + j; //3
}
}
1.时间复杂度为：1 + (N + 1) + N 我们按顺序分析一下
1 定义一次变量时间复杂度为1
N + 1 每次进行循环判定时间复杂度为N + 1，因为判断了N + 1次，最后一次没通过而已，但是依然算时间
N 循环变量递增每次都是1，n次就是N
2.时间复杂度为：N +N( N + 1) + NN
N 有第一个循环进入第二个循环一共是N次,所以定义变量jN次
N(N+1) 这个循环判断语句一样会执行N + 1次，在算上第一次循环到第二次循环为N次，所以为N(N+1)
NN 循环变量递增N次，第一次循环到第二次循环为N次，所以为NN
3.时间复杂度为NN
NN 每计算一次为1，第二个循环计算N次，第一个循环到第二次换选也为N次，所以为NN
时间复杂度是这样分析的，而不是记会的，很多自己写的程序不会分析时间复杂度，那是不行的
一、冒泡排序
原理
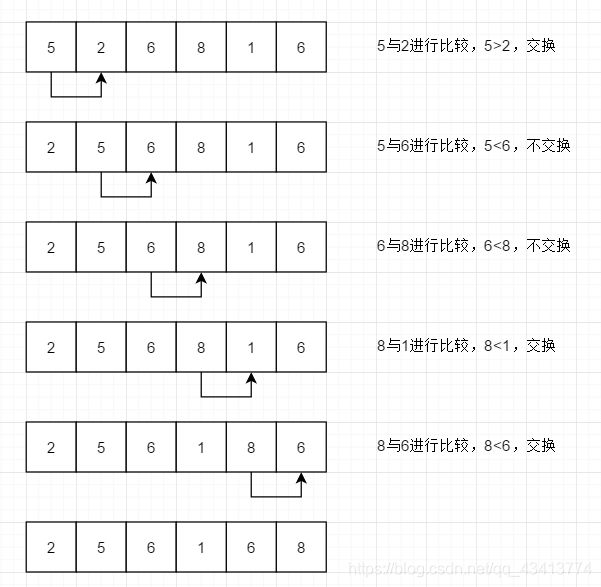
- 冒泡排序就是将相邻的两个元素进行比较，如果前者大于后者（反之降序），则交换，反之不交换。
图解
第一轮将最大值放在最后一位，第二轮将次大值防在倒数第二位
java代码：
public void bubblingSort(int[] nums) {
int n = nums.length;
for (int i = 0 ; i < n - 1; i++) {
for (int j = 0 ; j < n - 1; j++) {
if (nums[j] > nums[j + 1]) {
int temp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = temp;
}
}
}
}
二、直接插入排序
原理
- 插入排序从第二个元素开始，将数组分为有序和无序两部分，一直将所有元素都插入到有序序列当中。
图解
将数组分为有序和无序两部分，前一部分为有序，后一部分为无序
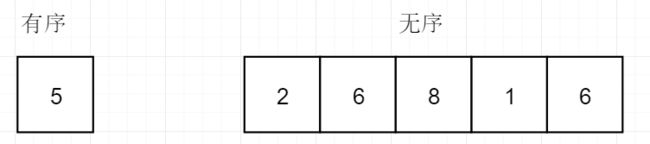
进行判断，由于2 < 5，所以5向后移动一个单位，2插到5的前面
继续进行判断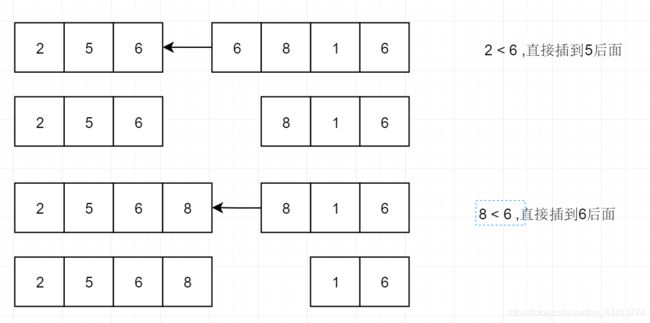
继续插入
继续插入
最终结果：
java代码：
public void insertSort(int[] nums) {
int n = nums.length;
for (int i = 1 ; i < n ; i++) {
int num = nums[i];
int preIndex = i - 1;
for (; preIndex >= 0 ; preIndex--) {
if (num < nums[preIndex]) {
nums[preIndex + 1] = nums[preIndex];
}
else break;
}
nums[preIndex + 1] = num;
}
}
三、希尔排序
原理
- 希尔排序其实就是直接插入排序的进阶版
- 由于插入排序的时间复杂度为O(n^2)，并不是那么的高效，所以我们对其进行了优化，我们将待排序列大部分元素变得有序，插入排序的工作量就会减少
- 在优化的时候我们用到了一个希尔增量，一般取数组长度的一半，下一次再去上次的一半，即n = n / 2
图示
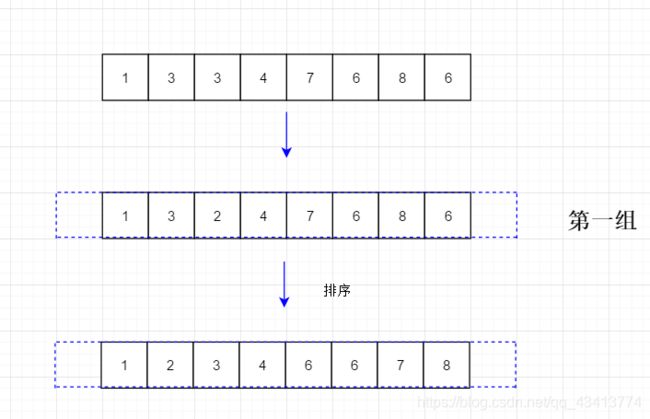
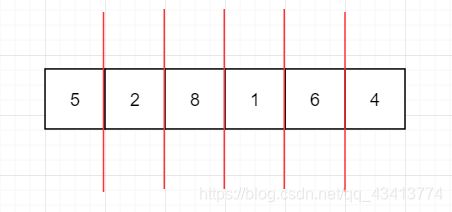
假设有如图这样一组序列
我们对其进行分组排序，对数组进行粗略的调整，就是让两个元素为一组，同组元素之间的跨度为数组总长的一半，即
8,2一组 / 6,4一组 /7,1一组/3,6一组
之后每组分别进行排序
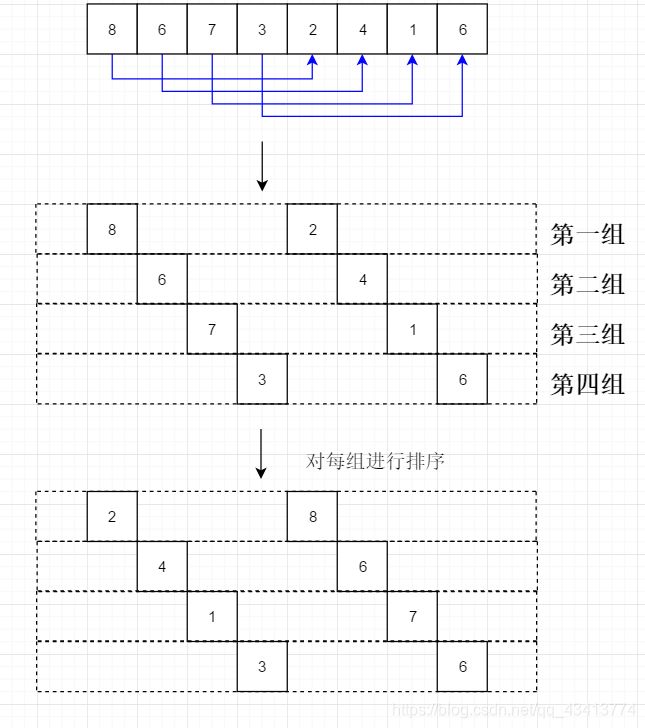
这样数组的顺序就会产生变化，然后在n = n / 2，以2为希尔增量，四元素为一组
以1为希尔增量，八元素为一组
java代码
public void shellSort(int[] arr) {
// 希尔增量n 每次缩减一半
for (int n = arr.length/2 ; n > 0 ;
n /= 2){
// 从第n个元素开始分组，并进行排序
for (int i = n ; i < arr.length ; i++){
//保存i，否则会出现越界
int j = i;
int temp = arr[j];
//对每一组进行插入排序
if (arr[j] < arr[j - n]){
while (j - n >= 0 && temp < arr[j - n]) {
arr[j] = arr[j - n];
j -= n;
}
//注意最后一定要找到插入的位置，然后赋值
arr[j] = temp;
}
}
}
四、选择排序
原理
- 找到当前序列的最大值（最小值），记录其所在位置，将其与最前面或者最后面的元素进行交换，使这个最大值（最小值）上浮（下沉）本次序列的最前面（最后面），从而完成一趟排序。下一趟排序时，已经有序的序列不参与。
- 和插入排序有相似性，将序列分为有序序列和无序序列两部分。
图解
第一趟排序
第二趟排序有序序列不参与，从5开始。
Java代码：
public void selectSort(int[] nums) {
int n = nums.length;
for (int i = 0 ; i < n ; i++) {
for (int j = i + 1 ; j < n ; j++) {
if (nums[i] > nums[j]) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
}
}
五、快速排序
原理
- 快速排序是对冒泡排序的一种改进。它的基本思想是通过一次排序将数据分隔成两部分，其中一部分中的所有数据比另一部分的所有数据都要小，之后再对这两部分分别进行快排，最终变成有序序列。
图解
例如数组
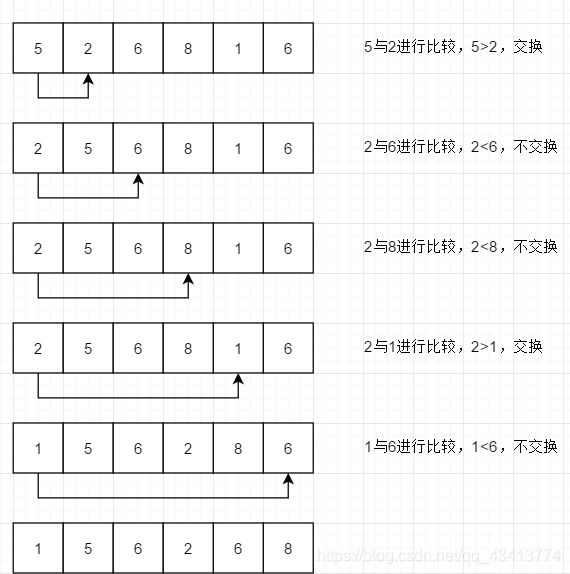
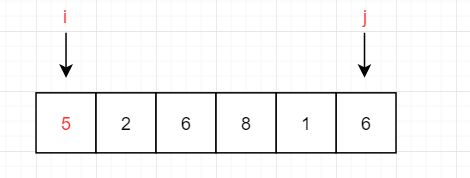
我们将第一位5作为一个基本数，用一个变量key将它存储起来，否则他会消失
- 我们将大于5的数字都放在5右边，小于5的都放在5的左边
- 使用双指针头部为指针i，尾部为指针j
第一次：6 > 5，放右边，移动指针j，j–
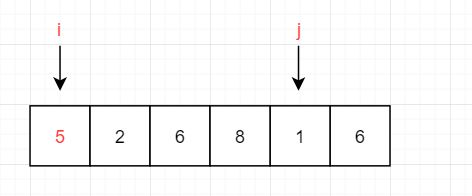
第二次：1 < 5,放左边，用nums[j]覆盖nums[i]，即nums[i] = 1，之后移动指正i，i++
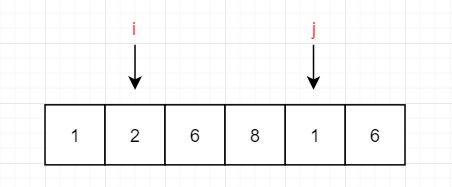
第三次：2 < 5，放左边，移动指针i，i++
第四次：6 > 5 ，放右边，用nums[i]覆盖nums[j]，即nums[j] = 6，移动指针j，j–
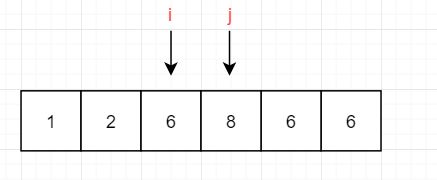
第五次：8 > 6，放右边，移动指针j，j–；这时候i = j，排序结束，这只是第一趟，我们还需要将两部分分别进行快排，我在这个可以使用递归，直到不可再分
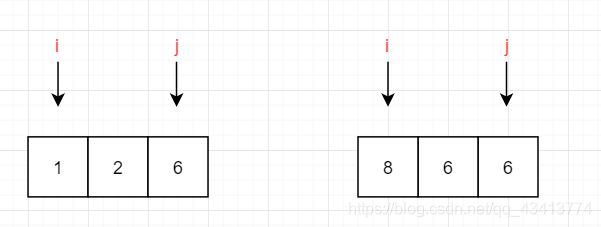
java代码：
public void quickSort(int[] nums , int start , int end) {
if (start < end ) {
//找到基准数
int key = nums[start];
//头指针
int i = start;
//尾指针
int j = end;
//终止条件为i = j
while (i < j) {
//先找比标准数大的值，如果不符合条件，继续移动j
while (i < j && nums[j] >= key) {
j--;
}
//结束循环的时候，已经找到了需要替换的位置
//右边的数字换到左边
nums[i] = nums[j];
while (i < j && nums[i] <= key) {
i++;
}
nums[j] = nums[i];
}
//最后将基准数放进去
nums[i] = key;
//继续快排前半部分
quickSort(nums , start , i);
//继续快排后半部分
quickSort(nums , i + 1 , end);
}
}
六、归并排序
原理
- 将已经有序的子序列合并，得到完全有序的序列；即使每个子序列有序，再使每个子序列间有序。
图解
我们一直两个子序列[1,5,9]和[2,4,6]，他们本事是有序的，将他们合起来就是无序的，我们现在要将他们变得有序。
我们首先定义一些变量作为标记
- L为新数组最左边位置，R为最右边位置
- L - M为数组left的长度，R-M+1为数组right的长度，M为中间长度
- i来表示数组left的下标位置，j来表示数组right的下表位置，k来表示数组nums的下标位置
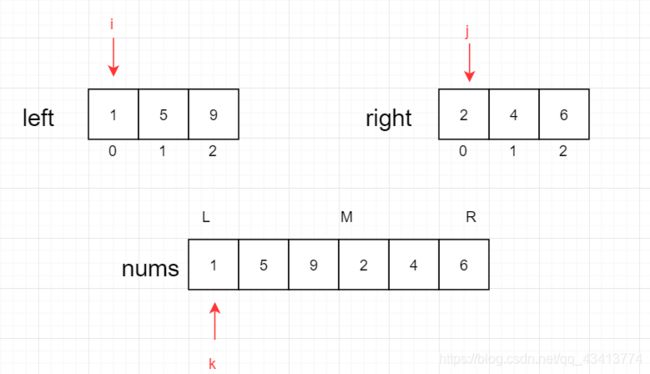
1.我们将i和j指向的值进行比较，1<2,即left[i] < right[j]，nums[k] = 1,i++,j++
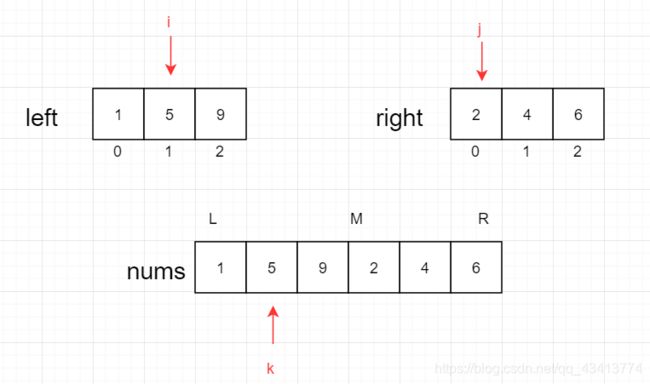
2.继续比较，5 > 2,即left[i] > right[i],nums[k] = 2,k++,j++
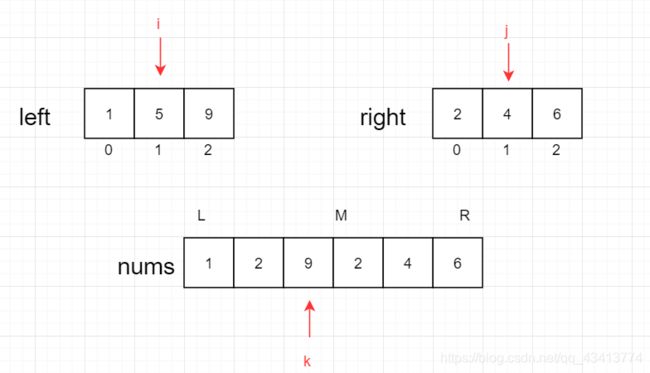
3.就这样一直比较下去…其实就是俩个数组的数据进行比较，形成一个新的有序数组
这种情况我们称为二路归并
但是如果给你一个序列你一刀没办法分出俩个有序序列呢？
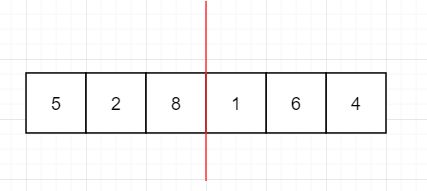
遇到这种情况，我们继续砍，直到只有一个元素，一个序列一定是有序的
这中情况被我们称为多路并归
java代码（二路归并）：
public void mergeSort(int[] nums){
int L = 0;
int R = nums.length - 1;
int M = R / 2 + 1 ;
int[] left = new int[M - L];
int[] right = new int[R - M + 1] ;
//为了新手方便理解，我将两个有序序列都放在了一个新的数组上
for (int i = 0 ; i < left.length ; i++) {
left[i] = nums[i];
}
for (int j = 0 ; j < right.length ; j++) {
right[j] = nums[M + j];
}
int i = 0 , j = 0 ,k = 0;
//注意：不能超出两数组的范围
while (i < left.length && j < right.length) {
nums[k++] = left[i] > right[j] ? right[j++] : left[i++];
}
//由于可能出现一种情况，right数组的所有元素都小于left数组的第一个元素，所有我们要将left数组里的元素跟到后面
while (i < left.length) {
nums[k++] = left[i++];
}
while (j < right.length) {
nums[k++] = right[j++];
}
}
七、堆排序
要了解大顶堆和小顶堆，我们先简单了解一下堆排序。
堆排序（Heapsort）是指利用堆这种数据结构设计的一种排序算法，堆积是一个近似完全二叉树的结构，并同时满足堆积的特性：子节点的键值或者所以总是大于或大于它的父节点（注意：父节点的左节点不一定大于右节点）。
我们还要注意的一点是，我们在学习编程的时候最好把英文名字都记一下，是有好处的。
小顶堆
原理
- 小顶堆就是每节点的值都小于左右节点的值
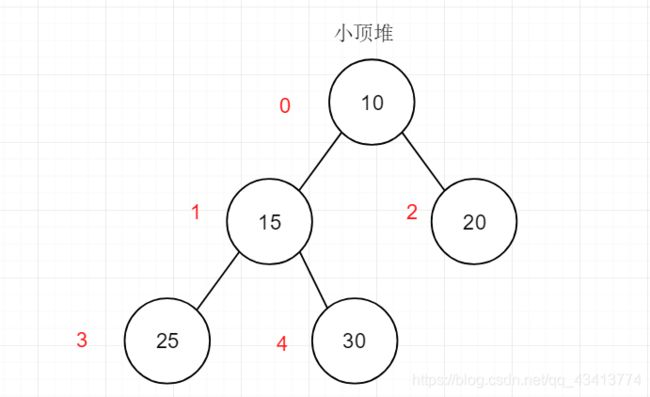
我们可以对堆中的节点按层进行编号，映射在数组中就是这样的
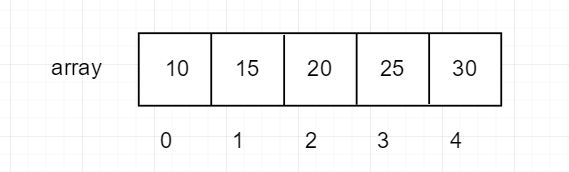
这个数组在逻辑上讲也是一个堆结构（小顶堆），我们用简单公式描述一个它的定义：
小顶堆：array[i] <= array[2i+1] && array[i] >=array[2i+2]
这里的i代表每个节点的键值或者索引，如果看不懂公式，将其代入上图示：
例如i = 0的时候，array[0] = 10,它的左节点为array[20+1],就是array[1] = 15，右节点array[20+2],即array[2] = 20;
此博客只有小顶堆图示，如果想了解堆排序具体步骤
图解
1.我们假设现在有一个无序序列，我们将无序序列构成一个小顶堆
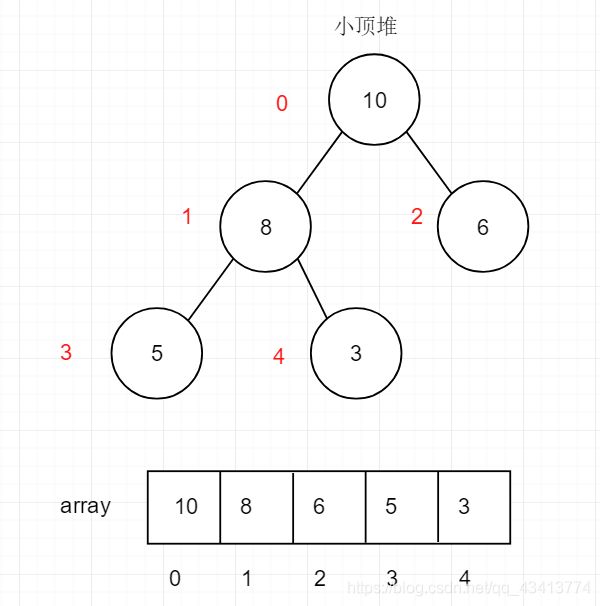
2.我们先从最后一个非叶子节点开始（叶子节点不用整理），一个非叶子节点为array.length/2 - 1 = 5 / 2 - 1 = 1 ，即8节点，从下至上，从左往右依次调整。
由于[8,5,3]中3最小，所以3和8交换
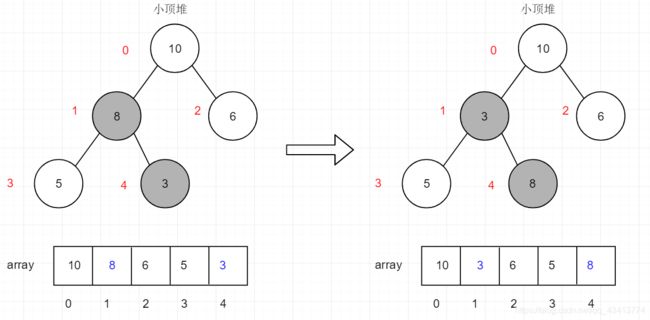
3.在找到第二个非叶子节点10，由于[10,3,6]中3最小，所以
和10交换
4.这时候导致[10,5,8]混乱，继续调整
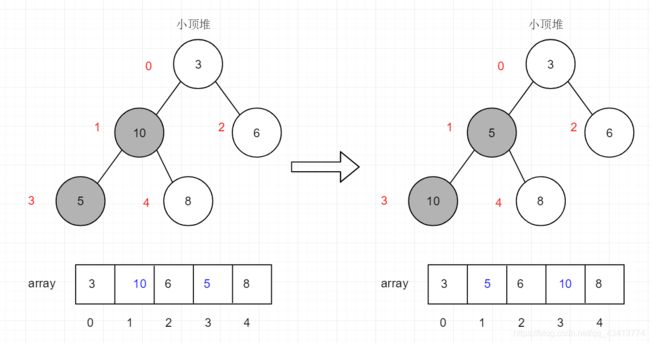
这样这个无序序列就构成了小顶堆（注意：只是构建成小顶堆，并不是有序序列）。
java代码（小堆顶）
/**
* 构造小顶堆
* @param arr 待调整数组
* @param size 调整多少
* @param index 调整哪一个 最后一个叶子节点的父节点开始调整
*/
public static void minHeap(int arr[], int size, int index) {
//左子节点
int leftNode = 2 * index + 1;
//右子节点
int rightNode = 2 * index + 2;
int min = index;//假设自己最小
//分别比较左右叶子节点找出最小
if(leftNode < size && arr[leftNode] < arr[min]) {//如果左侧叶子节点小于min则将最小位置换成leftNode并且递归需要限定范围为数组长度，
min = leftNode;//将最小位置改为左子节点
}
if(rightNode < size && arr[rightNode] < arr[min]) {//如果左侧叶子节点小于min则将最小位置换成rightNode
min = rightNode;//将最小位置改为右子节点
}
//如果不相等就需要交换
if(min != index) {
int tem = arr[index];
arr[index] = arr[min];
arr[min] = tem;
//如果下边还有叶子节点并且破坏了原有的堆。需要重新调整
minHeap(arr, size, min);//位置为刚才改动的位置；
}
}
/**
* 需要将最小的顶部与最后一个交换
* @param arr
*/
public static void heapSort(int arr[]) {
int start = (arr.length - 1)/2;//开始位置最后一个非叶子节点，最后一个叶子节点的父节点
for(int i = start; i>=0; i--) {
minHeap(arr, arr.length, i);
}
//最后一个跟第一个进行调整
for(int i = arr.length-1; i > 0; i--) {
int temp = arr[0];//最前面的一个
arr[0] = arr[i];//最后一个
arr[i] = temp;
//调整后再进行小顶堆调整
minHeap(arr, i, 0);
}
}
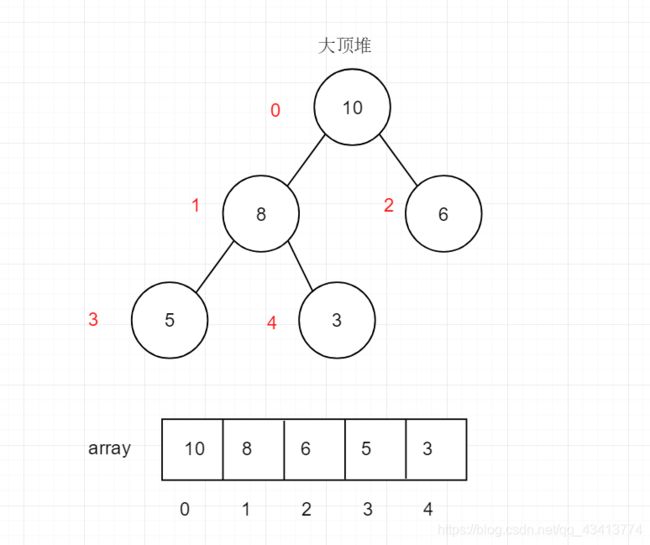
大顶堆
- 大顶堆就是和小顶堆相反，每个节点的值都大于其左右子节点
大堆顶就不细讲了，和小堆顶一个道理
八、桶排序
原理
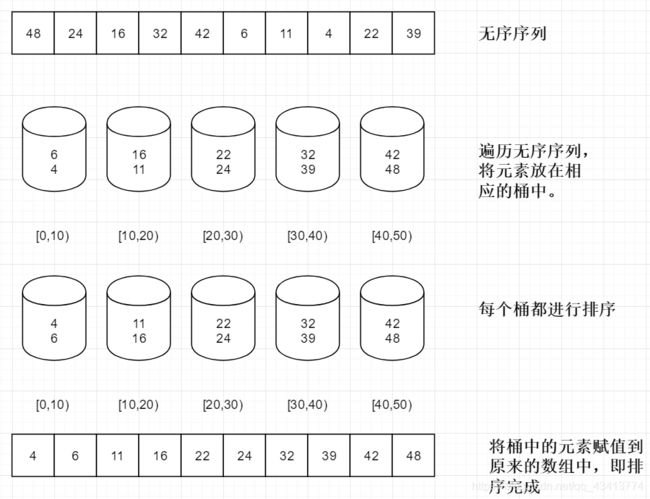
- 桶排序其实原理非常简单，就是划分了多个范围相同的区间，每个区间自动排序，最后合并
- 说到底桶排序重要的是它的思想，而不是它的实现，它是一种空间换取时间的排序。
- 假设一组数组有一w个元素甚至更多，不管你使用哪种排序都会非常的耗时，桶排序会将其分为好多个部分，分别进行排序，最后合起来，所以说它是空间换取时间。
图解
java代码：
public void bucketSort(int[] nums) {
//找出这个无序序列中的最大值
int max = 0;
for (int i = 0 ;i < nums.length ; i++) {
max = Math.max(max , nums[i]);
}
//划分桶的个数，我们这里假设每个桶的区间大小为10
int bucketNumber = max / 10 + 1;
//将桶放在一个容易里面，由你定义
List<List<Integer>> bucket = new ArrayList<List<Integer>>();
for (int i = 0 ; i < bucketNumber ; i++) {
bucket.add(new ArrayList<Integer>());
}
//将元素放入对应的桶中
for (int i = 0 ; i < nums.length ; i++) {
int index = nums[i] / 10 ;
bucket.get(index).add(nums[i]);
}
//对每个桶中的元素进行排序
for (int i = 0 ; i < bucket.size() ; i++) {
//在这里排序的方法你可以调用库函数，也可以自己写，可以是快排，也可以是插入
Collections.sort(bucket.get(i));
}
//最后将桶中的元素赋值到原来的序列中
int index = 0;
for (int i = 0 ; i < bucket.size() ; i++) {
for (int j = 0 ; j < bucket.get(i).size() ;j++) {
nums[index++] = bucket.get(i).get(j);
}
}
}
- 桶排序其实就是一个思想，很大意义上它并不算一个排序，它只能算是其他排序的进阶版，在面试的时候，面试官让你写完一个排序后他（她）可能会问你，我这里有1w个元素或者更多个，该怎么减少时间复杂度，这时候你就该想到桶排序
- 但桶排序也是有使用要求的，要求序列中的元素大小相差不是那么大，例如有这样一个数组[1,99999999]，这时候你不管怎么分，都会对内存造成巨大的浪费。
九、基数排序
原理
基数排序和桶排序其实是很相似的，他们都要用到桶，但区别是，基数排序的桶是固定的是10个桶，我们就在这10个桶里存放元素：
0 1 2 3 4 5 6 7 8 9
基数排序适合于有不同位数的大小数字，如25位两位数，568为三位数，89233为5位数。
通常我们第一轮将个位数相同的元素放在同一个桶中，例如：
0号桶：0,20
1号桶：1,21
第二轮将十位数相同的元素放在同一个桶中，例如：
0号桶：101 5（这里注意5的十位数也为0）
1号桶：16 49
图解
假设有这样一组序列
第一轮我们将个位数相同的元素放在同一个桶中，之后按列顺序取出，覆盖原理的数组
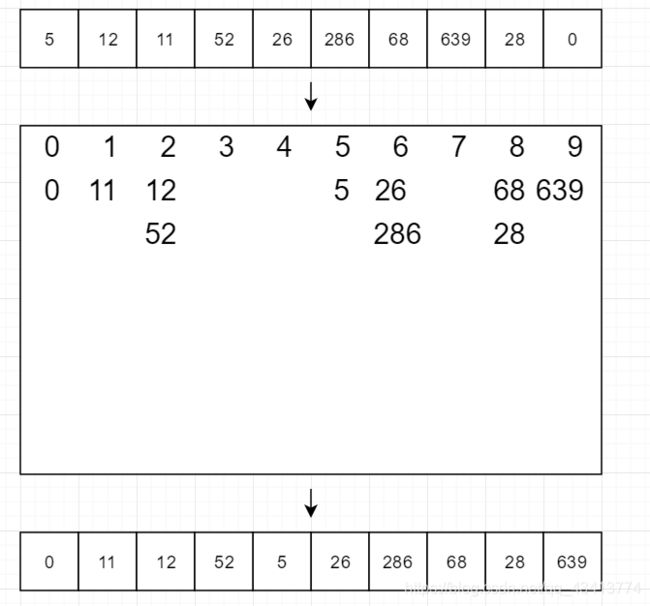
第二轮我们将十位数相同的元素放在同一个桶中，之后按列顺序取出，覆盖原理的数组
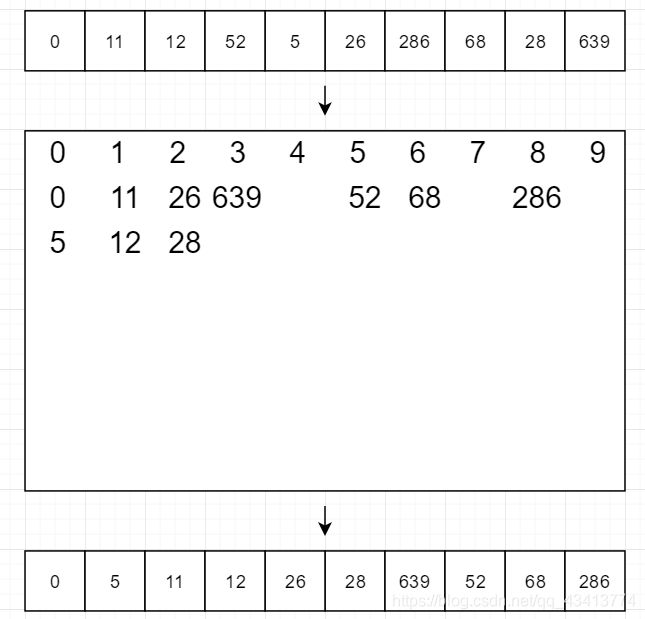
第二轮我们将百位数相同的元素放在同一个桶中，之后按列顺序取出，覆盖原理的数组
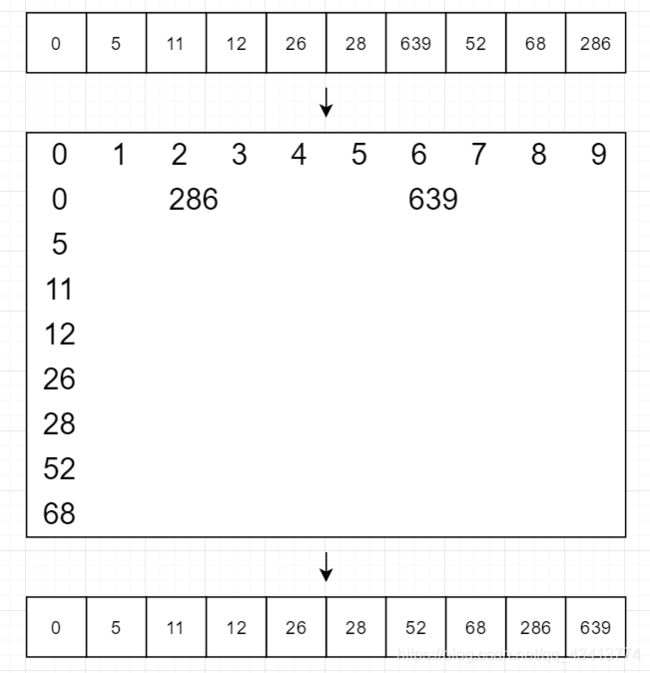
java代码：
public void radixSort(int[] nums) {
//找到数组中的最大值，以便知道循环的次数
int max = 0;
//找出最大值
for (int i = 0 ; i < nums.length ; i++) {
if (nums[i] > max) {
max = nums[i];
}
}
//计算最大值的位数，将最大值转换为字符串取长
int maxLength = (max + "").length();
//最坏的情况下，所给的序列个位数的大小相等，排在同一列，所以列大小为nums.length
int[][] arrs = new int[10][nums.length];
//记录元素的列位置
int[] counts = new int[nums.length];
//第一轮是个位数，第二轮是十位数，第三轮是百位数。。。。
for (int i = 0,n = 1 ; i < maxLength ; i++ , n*=10) {
for (int j = 0 ; j < nums.length ; j++) {
//取余
int remainder = (nums[j] / n) % 10;
//将相应元素放入二维数组
arrs[remainder][counts[remainder]] = nums[j];
//将该列的下标移动一个单位，方便下一个相应元素放入
counts[remainder]++;
}
//记录下标
int index = 0;
//每一轮循环之后都要将二维数组里的元素按列顺序放到原数组
for (int x = 0 ; x < counts.length ; x++) {
if (counts[x] != 0) {
for (int y = 0 ; y < counts[x] ; y++) {
//取出元素放入数组nums
nums[index++] = arrs[x][y];
}
//注意这里一定要把列元素个数清零，不然下一轮循环会出错
counts[x] = 0;
}
}
}
}
十、计数排序
原理
- 计数排序，顾名思义，对元素进行计数，然后进行排序，它适用于一定范围的整数排序
图解
假设有这样一组序列
我们取这组序列中的最大值，来确定辅助数组的大小，最大值为9，所以辅助数组的大小为10（0~9）
辅助数组下标即为待排序列中元素大小，辅助数组中的元素即为待排序列中元素出现的个数
我们进行循环将待排序列中的元素放入辅助元素
最后将输出辅助数组，以下标为元素大小，按顺序覆盖原数组
java代码：
public void countSort(int[] nums) {
//1.找出待排序列中的最大值
int max = 0;
for (int i = 0 ; i < nums.length ; i++) {
max = Math.max(max,nums[i]);
}
//2.确定计数数组的长度大小
int[] temp = new int[max + 1];
//3.将计数数组填充
for (int i = 0 ; i < nums.length ; i++) {
temp[nums[i]]++;
}
//4.覆盖原数组，从而得到有序序列
int index = 0;
for (int i = 0 ; i < temp.length ; i++) {
for (int j = 0; j < temp[i] ; j++) {
nums[index++] = i;
}
}
}
若有误，请指教！