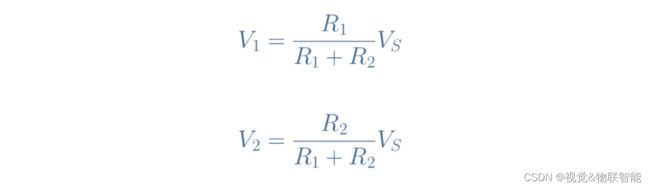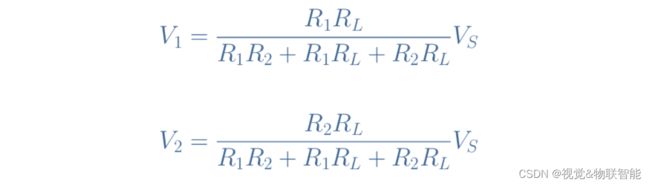【电路笔记】-分压器
分压器
文章目录
- 分压器
-
- 1、概述
- 2、负载分压器
- 3、分压器网络
- 4、无功分压器
-
- 4.1 电容分压器
- 4.2 感应分压器
- 5、总结
有时,需要精确的电压值作为参考,或者仅在需要较少功率的电路的特定阶段之前需要。 分压器是解决此问题的一个简单方法,因为它们利用了串联配置中的组件之间的电压可以下降的事实。
最常见的分压器类型是基于两个电阻器的串联组合,我们在本文的第一部分中详细介绍了这种类型的配置。
通过保持相同的架构,电阻器可以被电容器或电感器等电抗元件替代。 这些不同类型的分压器在另外两个部分中介绍。
1、概述
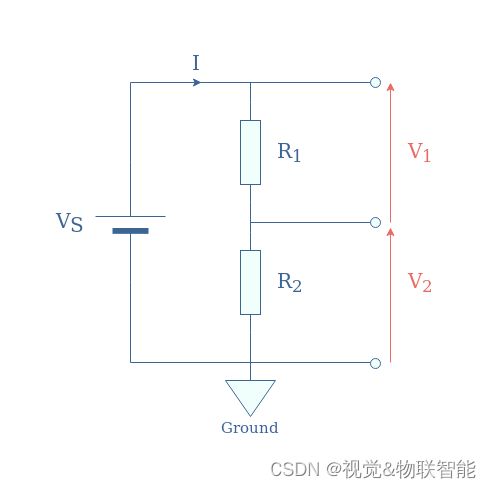
在图1中,我们展示了电阻分压器最常见、最简单的配置:
下面,我们将此配置标记为 R 1 − R 2 R_1-R_2 R1−R2。
首先我们可以注意到,根据基尔霍夫电压定律, V 1 + V 2 = V S V_1+V_2=V_S V1+V2=VS。 由于欧姆定律,该关系可以重写为 V S = ( R 1 + R 2 ) × I V_S=(R_1+R_2)\times I VS=(R1+R2)×I。由于 V 1 = R 1 × I V_1=R_1\times I V1=R1×I、 V 2 = R 2 × I V_2=R_2 \times I V2=R2×I 和 I = V S / ( R 1 + R 2 ) I=V_S/(R_1+R_2) I=VS/(R1+R2),我们在公式1 中得到 以下分压器公式:
有趣的是,公式1 中 V 1 V_1 V1 和 V 2 V_2 V2 的无量纲因子的范围都可以从 0 到 1。因此,信号 V 1 V_1 V1 和 V 2 V_2 V2 的范围可以从 0V 到源值 V S V_S VS。
通过数据程序,可以根据 R 1 R_1 R1 和 R 2 R_2 R2 绘制 V 1 V_1 V1 或 V 2 V_2 V2 可能取的每个可能值,如图 2 所示。在本例中,我们选择绘制 V 2 V_2 V2,其中 V S = 10 V V_S=10V VS=10V 且 R 1 , R 2 = [ 0 ; 300 ] Ω R_1,R_2= [0;300]\Omega R1,R2=[0;300]Ω。
通常,电压源或电流源只能提供固定值的电压或电流。 然而,电路的某些级需要源提供的较低值。
适当选择电阻值的简单分压器可以提供 0 V 和源值之间的任何电压值,它构成了在特定级之前衰减源的良好解决方案。
电阻分压器适用的另一个应用是高直流电压的测量。 我们在图 3 中说明了这种方法:
请注意,电阻器的形状是自愿修改的,以反映比率 R 1 / R 2 R_1/R_2 R1/R2。
为了保护电压表(及其用户)不直接测量高压 V S V_S VS,电压表只测量对应于 R 2 / ( R 1 + R 2 ) × V S R_2/(R_1+R_2)\times V_S R2/(R1+R2)×VS的一小部分。 然后通过将测量值乘以除高电压的相同值来校正显示。
例如,如果 R 1 / R 2 = 99 R_1/R_2=99 R1/R2=99,则电压表仅测量 V S V_S VS 的 1%。 然后,电压表将测量值乘以 100,在屏幕上显示 V S V_S VS 的准确值。
2、负载分压器
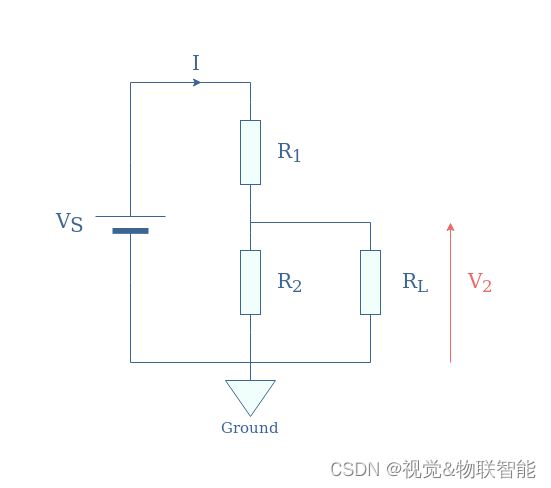
我们现在考虑与图1中所示相同的分压器 R 1 − R 2 R_1-R_2 R1−R2,但在 R 2 R_2 R2 端子处额外存在负载 R L R_L RL:
我们将演示 V 2 V_2 V2的表达式。 首先我们表示 R 2 / / R L R_2//R_L R2//RL并联组的等效电阻 R e q R_{eq} Req:
然后,我们将分压器的公式(公式 1)应用于分压器 R 1 − R e q R1-R_{eq} R1−Req:
如果我们开发并重新排列这个表达式,我们将获得 V 2 V_2 V2 作为 R 1 R_1 R1、 R 2 R_2 R2、 R L R_L RL 和 V S V_S VS 的函数。 此外,如果将输出负载改为连接到R1的端子,我们也可以类似地写出 V 1 V_1 V1的表达式,得到负载分压器的两个公式:
3、分压器网络
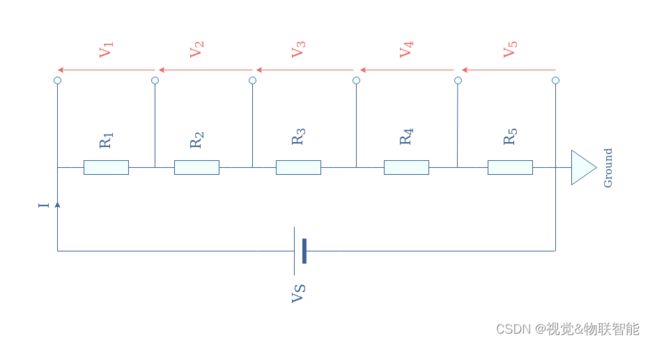
分压器网络是三个或更多串联电阻的组合,充当分压器。 在下图 5 中,我们展示了具有五个电阻器的分压器网络:
如果我们记下 R s e r i e s = R 1 + R 2 + R 3 + R 4 + R 5 R_{series}=R_1+R_2+R_3+R_4+R_5 Rseries=R1+R2+R3+R4+R5 电阻器串联组合的等效电阻,则每个电压由公式 3 给出:
对于具有 N N N 个电阻器的分压器网络,公式3 在 R s e r i e s = R 1 + R 2 + … + R N R_{series}=R_1+R_2+…+R_N Rseries=R1+R2+…+RN 时仍然有效。
我们需要通过说电阻分压器的效率非常低来结束有关电阻分压器的部分,因为电阻器通过焦耳加热来耗散功率。 出于与这些功率损耗相关的明显安全原因,它们仅用于低功率应用,例如在微电子中驱动 MOSFET 和双极放大器。
对于高功率应用,首选无功分压器,因为它们不会因焦耳加热而耗散太多功率。
4、无功分压器
替代分压器可以基于电容器或电感器而不是电阻器,它们被称为无功分压器。
4.1 电容分压器
电容分压器基于与之前图1 中所示相同的架构,只是用电容器替换了电阻器。 由于电容器的电抗由 1 / C ω 1/C\omega 1/Cω 给出,因此电容分压器仅在交流状态下工作。
使用电容器的优点是它们在高频下的功率损耗比电阻器低得多。 事实上,我们在有关交流电阻的专门文章中看到,由于趋肤效应,高频时交流阻抗往往比直流阻抗高得多。
此外,电容分压器通常用于 RMS 值高于 100 kV 的电压。 原因是电阻分压器在高电压下散发过多热量,而理想或接近理想的电容器以电场的形式存储能量并将其释放到电路中。
如果我们将 V 1 V_1 V1、 V 2 V_2 V2 和 V S V_S VS 标记为电压的 RMS 值,则很容易再次证明它们遵循公式 1 中所示的类似关系。但是,由于此处的阻抗与 1/C 成正比,因此 分子变化:
使用图3中的类似电路用电容器代替电阻器,适合测量高交流电压。 由于电容器的压降与 1 / C 1/C 1/C 成正比,因此小电容器 C 1 C_1 C1 中会出现较大的压降:
4.2 感应分压器
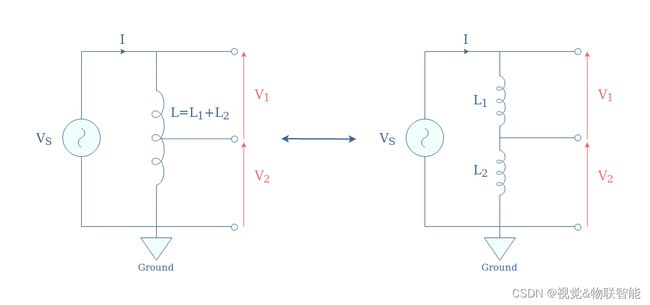
我们在文献中没有遇到“感应分压器”这个术语,但我们更愿意将该电路称为自耦变压器。 自耦变压器是具有多个抽头点的单个电感器,可以将其视为串联的多个电感器。在图8中,我们提出了一种具有一个中间抽头点的自耦变压器,这对应于更简单的设计,相当于串联的两个电感器 :
如果我们记下 N 1 N_1 N1 和 N 2 N_2 N2 为 L 1 L_1 L1 和 L 2 L_2 L2 中的绕组数量,则电压比可以简单地由 V 2 / V 1 = N 2 / N 1 V_2/V_1=N_2/N_1 V2/V1=N2/N1 给出。
与电容分压器类似,自耦变压器适用于高功率应用,因为电感器以磁场的形式存储能量并将其释放到电路,不产生热量耗散。
当绘制为等效“感应分压器”时,自耦变压器的电压公式由公式5给出:
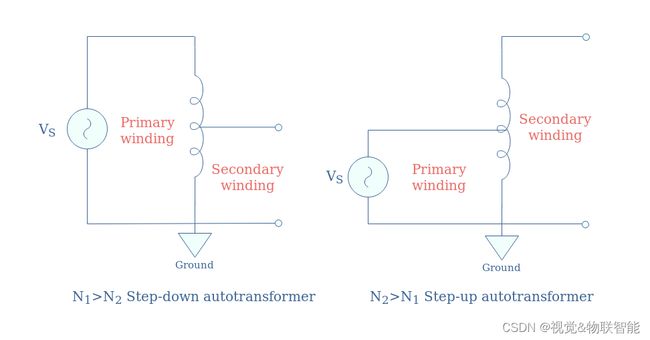
通常,自耦变压器最常见于高功率传输线路中,用于降压或升压。 降压和升压自耦变压器很容易通过其初级和次级绕组的比例来识别:
5、总结
- 任何分压器均由至少两个串联配置的组件组成,其中可能会发生压降。 输出取自分接点和电路参考(接地)之间。
- 此类电路的目标是获得比源电源 V S V_S VS 更小的电压输出值,以便尊重电路输入级的动态。 输出对应于源的一部分,介于 0 和 V S V_S VS 之间。
- 对于低功耗应用,我们依靠基于电阻元件的电阻分压器。 我们详细介绍了输出电压公式的演示、输出负载提供的修改以及电压网络分压器的存在,其中许多电阻器可以串联互连以同时提供不同的电压输出。
- 电阻分压器的缺点是不适合电网配电等大功率应用。 对于此功能,优选无功分压器,因为它们不会散发大量热量,例如电阻器。
- 无功分压器分为两类:电容式分压器和电感式分压器,具体取决于使用的基本元件。 对于电容分压器,电容器串联连接,最大的电压降出现在最小的电容器中,因为它们的电抗与其电容成反比。
- 感应分压器最常被称为自耦变压器,与电阻分压器类似,最大的电压降发生在最大的电感器中,因为它们的电抗与其电感成正比。
- 电容式分压器主要用于万用表中以探测高电压,而电感式分压器则用于电网配电中以降压或升压 50 Hz 高压。 一个典型的例子是自耦变压器在传输线路中不一定使用相同电压的国家之间建立联系。