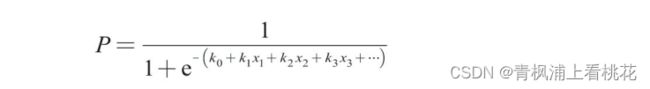机器学习逻辑回归算法原理与python代码实现入门

一、原理

        逻辑回归模型本质就是将线性回归模型通过Sigmoid函 数进行了一个非线性转换，得到一个介于0～1之间的概率值。

对于二分 类问题（分类0和1）而言，其预测分类为1（或者说二分类中数值较大 的分类）的概率可以用如下所示的公式计算。

 

因为概率和为1，则分类为0（或者说二分类中数值较小的分类）的 概率为1-P。

逻辑回归模型的本质就是预测属于各个分类的概率，有了概率之 后，就可以进行分类了。对于二分类问题来说，例如在预测客户是否会 违约的模型中，如果预测违约的概率P为70%，则不违约的概率为 30%，违约概率大于不违约概率，此时就可以认为该客户会违约。对于 多分类问题来说，逻辑回归模型会预测属于各个分类的概率（各个概率 之和为1），然后根据哪个概率最大，判定属于哪个分类。 了解了逻辑回归模型的基本原理后，在实际模型搭建中，就是要找 到合适的系数ki和截距项k0，使预测的概率较为准确，在数学中使用极 大似然估计法来确定合适的系数ki和截距项k0，从而得到相应的概率。

在Python中，已经有相应的库将数学方法整合好了，通过调用库中的模 块就能建立逻辑回归模型，从而预测概率并进行分类。下面通过一个简 单的案例来说明如何在Python中快速搭建逻辑回归模型，以帮助大家加 深对逻辑回归模型的理解。

二、逻辑回归python实现

1.简单案例

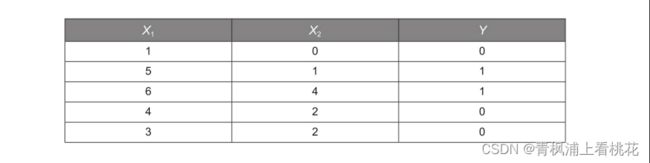
本小节通过一个简单的Python案例来说明逻辑回归模型的算法原 理，数据见下表。特征变量有2个——X1和X2；Y是目标变量，取值为0 或1，代表2个不同的分类。以客户违约预测模型为例，可以把特征变量 X1看成收入，X2看成历史违约次数，目标变量Y看成是否违约（0表示 不违约，1表示违约）。

先构造数据，代码如下。

1 X = [[1, 0], [5, 1], [6, 4], [4, 2], [3, 2]]

2 Y = [0, 1, 1, 0, 0]

再将已有数据使用逻辑回归模型进行拟合，代码如下。

1 from sklearn.linear_model import LogisticRegression

2 model = LogisticRegression()

3 model.fit(X, Y)

第1行代码从Scikit-Learn库中引入逻辑回归模型 LogisticRegression。

第2行代码将逻辑回归模型赋给变量model，这里没有设置参数，即 使用默认参数。

第3行代码用fit()函数进行模型的训练。

训练完模型之后，即可用模型的predict()函数进行预测，代码如 下。

1 model.predict([[2, 2]])

预测结果如下。

1 [0]

       有的读者可能会感到疑惑：为什么上述代码中的predict()函数中要 写两组中括号，而不是写成model.predict（[2,2]）呢？这是因为predict() 函数默认接收一个多维数据，将其用于同时预测多个数据时大家会更容 易理解，演示代码如下。

1 model.predict([[1, 0], [5, 1], [6, 4], [4, 2], [3, 2]])

因为这里演示的多个数据和变量X是一样的，所以也可以直接写成 model.predict（X），预测结果如下。

1 [0 1 1 0 0]

可以看到其预测准确度为100%。

 2.用逻辑回归模型处理多分类问题

1 # 构造数据，此时y有3个分类-1、0、1

2 X = [[1, 0], [5, 1], [6, 4], [4, 2], [3, 2]]

3 y = [-1, 0, 1, 1, 1] 4 5

# 模型训练

6 from sklearn.linear_model import LogisticRegression

7 model = LogisticRegression() 8 model.fit(X, y)

模型训练完成后，同样可以用predict()函数进行分类预测，代码如 下。

1 print(model.predict([[0, 0]])) 打印结果如下。

1 [-1]

同样可以用predict_proba()函数获取各个分类的概率，代码如下。

1 y_pred_proba = model.predict_proba([[0, 0]])

 打印结果如下。

可以看到预测分类为-1的概率最大，因此数据[0，0]被预测为分 类-1。