【Python】Python实现LRU_Cache
题目
1.给出斐波那契数列的递归解法,找一种方法优化该函数
2.如果我们的空间有限怎么办?也就是说当内存有限的时候,我们需要有一种策略来解决缓存已满的问题。
常规优化法就是给他加上一个数组来存储已经计算过的值,避免重复计算
Pythonic的写法是给他加上一个装饰器,
装饰器的思路:用一个字典来缓存已经计算过的内容,如果传过来的参数在我们的保存结果里面就可以直接返回,如果不在则先去调用原来的函数计算出结果,存储到缓存队列中,并将结果返回
这样即使当n很大的时候也可以很快的计算出斐波那契数列的值
#coding:utf-8
def cache(func):
data = {}
def wrapper(n):
if n in data:
return data[n]
else:
res = func(n)
data[n] = res
return res
return wrapper
@cache
def fib(n):
if n < 2:
return n
else:
return fib(n - 1) + fib(n - 2)
for i in range(1, 10):
print(fib(i))
如果我们的空间有限怎么办?也就是说当内存有限的时候,我们需要有一种策略来解决缓存已满的问题。
最常见的缓存置换策略有LRU和LFU
LRU表示最近最少使用算法,是把最远访问的元素剔除
LFU表示最不经常使用算法,是把使用频率最少的元素剔除
依据局部性原理以及缓存都会有热数据,很有可能最近使用过的元素还会很快被再次使用到,所以当内存有限的时候,我们一般都会使用LRU来做缓存。
这个时候我们需要手动实现一个LRU
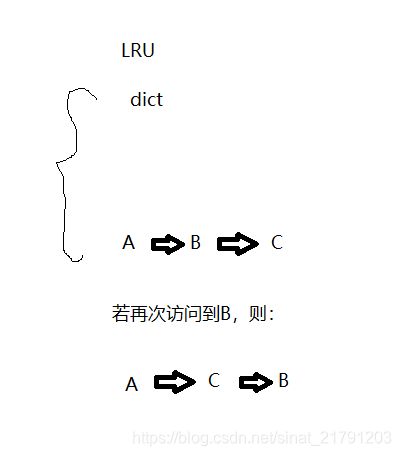
刚才比较直观,我们直接用dict来缓存已经计算过的数据,但是我们怎样来实现一个LRU把最远访问的元素剔除呢?
最常规的想法就是有一个链表每次访问key的时候都将他们的访问顺序记录下来,如果再次被访问到的时候就需要把他放在最前面这样的话最早访问的元素还是在链表的最左端,这样每一次当缓存满了的时候就可以直接将最左端的元素剔除。
但实际上用单链表的话会有很大的问题,就是如果你要找到一个元素并删除他,时间复杂度是O(n),因为单链表的查找需要从头遍历到尾才能找到目标元素。不过如果用双链表的话就可以在时间复杂度为O(1)的情况下找到要删除的元素,并将其删除。
如果要删除双链表中的结点,则只需将该结点的前一个结点的next指针指向该结点的下一个结点,将该结点的下一个结点的prev指针指向该结点的前一个结点,只需要两步操作,所以双链表删除一个结点需要的时间复杂度是O(1)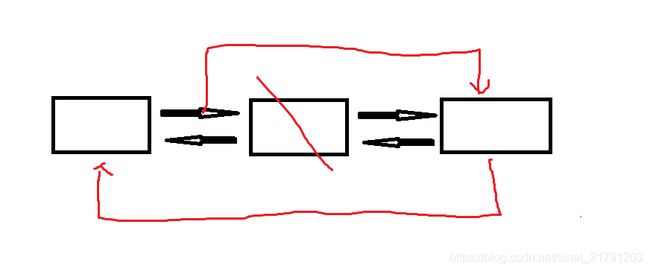
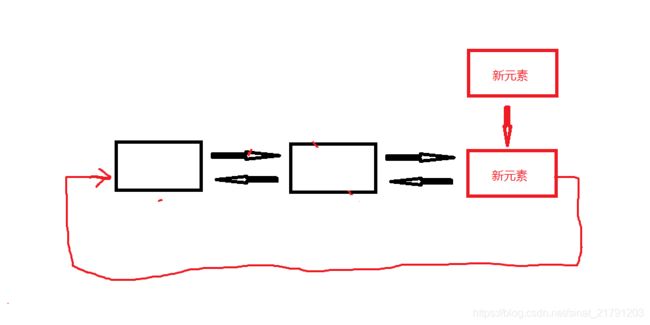
如果需要在双链表中添加元素,原链表最后一个结点的next指针指向新元素,新元素的prev指针指向原链表的最后一个结点,新元素的next指针指向原链表的第一个结点,实际上这样的话就构成了一个环形双向链表
下来我们检测一下是否能满足要求
记录一下操作,假如访问顺序order是A, B, C, B,缓存的字典dict的size只有两个,然后用access记录访问顺序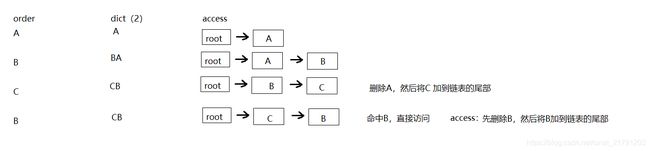
接下来实现一个双端队列
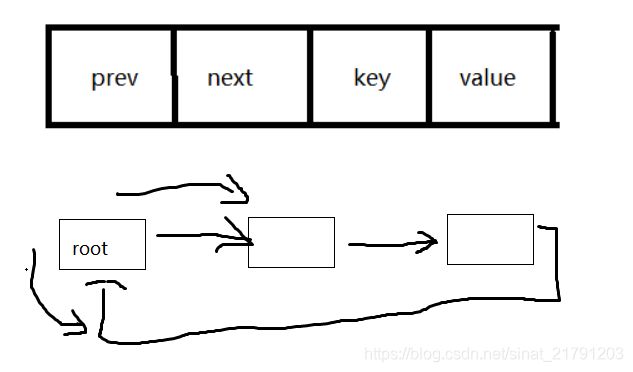
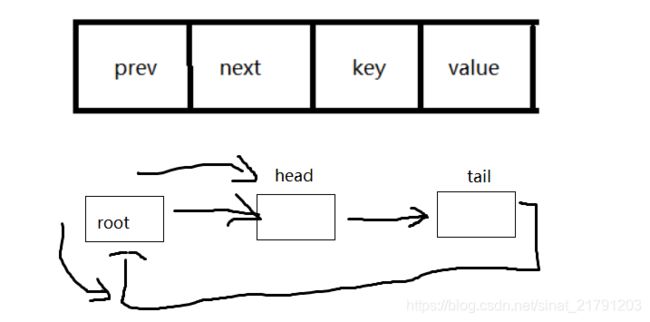
首先有一个root结点,然后对应每一个结点都是有四个元素,根节点指向下一个结点,最后一个结点指向首节点,这样的话可以通过根节点查找他的下一个结点,查找他的最后一个结点
接下来跟着这个思路实现一下
首先实现一个叫做结点Node,表示链表结点
四个结点默认值为none,因为下边实现循环双端队列定义一个root结点,需要指向他自己
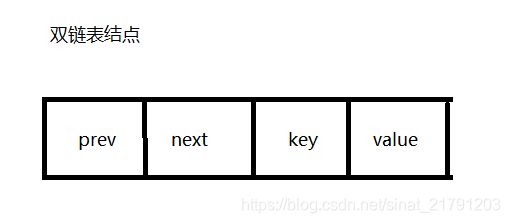
# 双链表结点
class Node(object):
def __init__(self, prev=None, next=None, key=None, value=None):
self.prev, self.next, self.key, self.value = prev, next, key, value实现一个循环双端队列
定义一个根节点
定义操作,首先我们可以看到在刚才访问的时候,有删除和append操作,以及访问第一个节点,首尾节点的操作
访问首节点head,尾结点tail,
访问头结点head,返回root结点的下一个结点,
访问尾结点tail,返回root结点的上一个节点
接下来还需要实现两个操作,删除,追加到结尾
定义两个操作,
一个是remove操作,即删除一个结点
删除结点的话先考虑一个特殊情况,如果这个结点本身就是根节点的话,就什么都不需要做否则的话来考虑如何删除一个结点,删除结点的话需要把前一个节点跟后一个结点连接起来,具体操作就是,把当前结点的上一个结点的next指针指向当前结点的下一个结点,将当前结点的下一个结点的prev指针指向当前结点的上一个结点。
一个是append操作,即追加一个结点
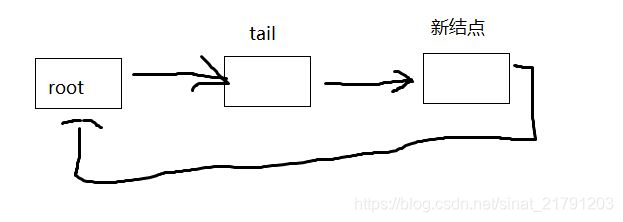
当我们需要追加一个新结点的时候,我们需要将原链表末尾的结点tail的next指针指向新结点,将新结点的next指针指向root结点。将root结点的prev指针指向新结点
# 循环双端链表
class CircleDoubleLinkedList(object):
def __init__(self):
node = Node()
# 该结点的prev指针和next指针都指向它自己
node.prev, node.next = node, node
# 给他一个根节点
self.rootnode = node
# 访问首结点head结点,返回root结点的下一个结点
def headnode(self):
return self.rootnode.next
# 访问尾结点tail,返回root结点的上一个节点
def tailnode(self):
return self.rootnode.prev
# 删除一个结点
def remove(self, node):
if node is self.rootnode:
return
else:
node.prev.next = node.next
node.next.prev = node.prev
# 追加一个结点的操作
def append(self, node):
tailnode = self.tailnode()
tailnode.next = node
node.next = self.rootnode
self.rootnode.prev = node
接下来实现LRUcache,用类来实现,因为他会有一些属性,用类的话我们可以用成员来保存他
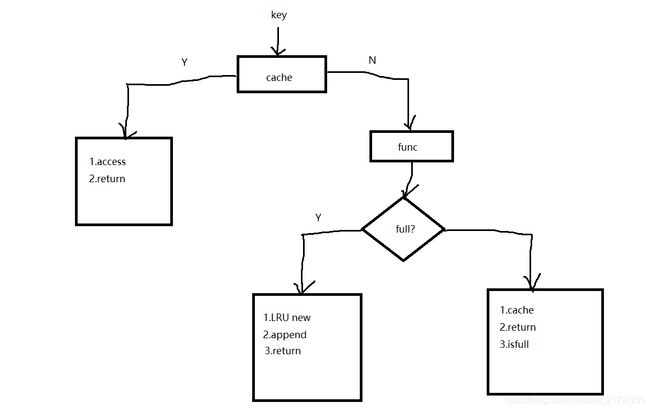
定义完属性之后来写装饰器,先画一个流程图
如果有一个key值进来,我们需要先查看cache中有没有缓存
如果有则:
1.更新access顺序
2.返回结果
如果没有在缓存中则需要先调用原来的function,计算出来结果
然后查看缓存是否已满,如果已满则将1.缓存更新new,2.将新结点加入access中
如何实现一个装饰器
伪代码:
def wrapper(n):
-
首先拿一下缓存的结点cachenode
-
命中:
-
-
如果cachenode不是None则说明命中缓存:
-
如果命中则需要将当前结点移到双端链表的尾端,表示该结点是最新访问过的
-
具体操作是:
-
先删除当前结点,
-
再将当前结点append到双端链表的尾部
-
返回结果值cachenode.value
-
-
未命中
-
缓存未满:
-
-
-
-
将原链表的尾结点tailnode拿出来
-
构造一个新结点newnode,该结点的prev指针指向原链表的尾结点tailnode,next指针指向原链表的根节点rootnode,key是传入的参数n,值value是刚才调用函数计算的结果值value
-
将该结点缓存到cache中去,即append到原双端链表的尾部
-
更新一下isfull是否已满,即判断当前缓存的长度是否大于等于最大值
-
返回newnode的value值
-
-
缓存已满:
-
-
-
-
取出要删除的结点lru_node,也就是头结点,即root结点指向的下一个结点
-
删除最远结点的key值
-
删除最远的结点lru_node,
-
将原链表的尾结点tailnode拿出来
-
构造一个新结点newnode,方法同上
-
将新结点加入到当前链表的尾部
-
将新结点的值缓存下来
-
返回结果值
-
-
代码:
#coding:utf-8
def cache(func):
data = {}
def wrapper(n):
if n in data:
return data[n]
else:
res = func(n)
data[n] = res
return res
return wrapper
# 双链表结点
class Node(object):
def __init__(self, prev=None, next=None, key=None, value=None):
self.prev, self.next, self.key, self.value = prev, next, key, value
# 循环双端队列
class CircleDoubleLinkedList(object):
def __init__(self):
node = Node()
# 该结点的prev指针和next指针都指向它自己
node.prev, node.next = node, node
# 给他一个根节点
self.rootnode = node
# 访问首结点head结点,返回root结点的下一个结点
def headnode(self):
return self.rootnode.next
# 访问尾结点tail,返回root结点的上一个节点
def tailnode(self):
return self.rootnode.prev
# 删除一个结点
def remove(self, node):
if node is self.rootnode:
return
else:
node.prev.next = node.next
node.next.prev = node.prev
# 追加一个结点的操作
def append(self, node):
tailnode = self.tailnode()
tailnode.next = node
node.next = self.rootnode
self.rootnode.prev = node
class LRUCache(object):
def __init__(self, maxsize=16):
self.maxsize = maxsize
# 字典存储结果
self.cache = {}
# 循环双端链表
self.access = CircleDoubleLinkedList()
# 将访问key的数据记录下来,
# 标识记录缓存是否已经满了
# 看一下当前缓存中的数据个数是否大于maxsize
length_cache = len(self.cache)
print(type(length_cache))
print(type(self.maxsize))
self.isfull = len(self.cache) >= self.maxsize
# 接下来看如何实现一个装饰器
def __call__(self, func):
def wrapper(n):
# 首先拿一下缓存的结点
cachenode = self.cache.get(n)
# 如果cachenode不是None则说明命中缓存
if cachenode is not None: # hit
# 如果命中则需要将当前结点移到双端列表的尾端,表示他是最新访问的
# 删除当前结点
self.access.remove(cachenode)
# 将当前结点append到双端链表的尾部
self.access.append(cachenode)
# 返回结点值cachenode.value
return cachenode.value
# 如果cachenode不是None则说明未命中
else: #miss
# 先调用函数计算出结果值
value = func(n)
# case1缓存未满
if not self.isfull:
tailnode = self.access.tailnode()
newnode = Node(tailnode, self.access.rootnode, n, value)
self.access.append(newnode)
self.cache[n] = newnode
self.isfull = len(self.cache) >= self.maxsize
return value
else: #full
lru_code = self.access.headnode()
del self.cache[lru_code.key]
self.access.remove(lru_code)
tailnode = self.access.tailnode()
newnode = Node(tailnode, self.access.rootnode, n, value)
self.access.append(newnode)
self.cache[n] = newnode
return value
return wrapper
@LRUCache()
def fib(n):
if n < 2:
return n
else:
return fib(n - 1) + fib(n - 2)
for i in range(1, 10):
print(fib(i))Reference
1.B站大佬视频讲解