小程序中的大道理之三--对称性和耦合问题
再继续扒
继续 前一篇 的话题, 在那里, 提到了抽象, 耦合及 MVC, 现在继续探讨这些, 不过在此之前先说下第一篇里提到的对称性.
注: 以下讨论建立在前面的基础之上, 为控制篇幅起见, 这里将不再重复前面说到的部分, 如果您还没看过前两篇章, 阅读起来可能会有些困难.
这是第一篇的链接小程序中的大道理
对称性(Symmetry)
这里先说下对称性的问题. 问题中的图案是左右对称的, 但到目前为此, 我们的代码却不是对称的, 输出之所以对称原因在于空格与背景之间难以区分.
让我们换个符号, 比如脱字符"^", 再输出一下, 就可以看出不对称来, 因为在右边我们输出星号后就直接换行了:
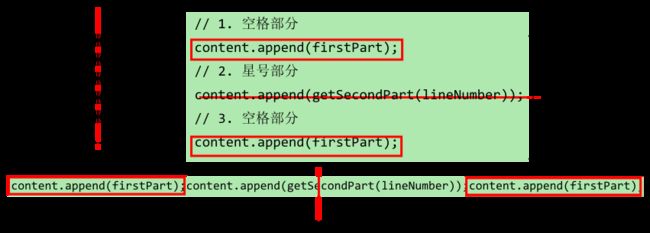
只要稍微调整一下程序, 在输出换行之前再输出一下空格(或者现在的脱字符"^"), 就能满足对称的输出了:
private String getLineContent(int lineCount, int lineNumber) {
StringBuilder content = new StringBuilder();
String firstPart = getFirstPart(lineCount, lineNumber);
// 1. 空格部分
content.append(firstPart);
// 2. 星号部分
content.append(getSecondPart(lineNumber));
// 3. 空格部分
content.append(firstPart);
// 4. 换行部分
content.append(System.lineSeparator());
return content.toString();
}
这样之后, 图案是左右对称, 反映在程序上就呈现出上下对称了. 当然也可以把三个语句写在一行里, 这样它也左右对称了:
程序是对客观世界的问题的一种映射, 因此程序的结构反映了问题的结构.
当然了, 如果你的程序写得很松散, 结构, 层次不清晰, 就不太容易看出这种对称来.
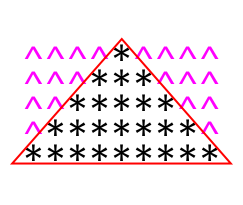
不知道是否有人意识到了, 在前面我有意无意地忽略了另一个对称问题. 这就是星号的对称, 在上图中只是把它当成对称轴看待.
撇开什么脱字符"^"或者空格, 其实单纯由星号构成的三角形也是对称的, 这是更主要的一个对称:
这种对称又来自哪里呢? 让我们深入到 getSecondPart 里面去:
private String getSecondPart(int lineNumber) {
int count = getElementCountOfSecondPart(lineNumber);
StringBuilder part = new StringBuilder();
for (int i = 0; i < count; i++) {
part.append(" ");
}
return part.toString();
}
很遗憾, 你看不到什么对称. 继续深入到 getElementCountOfSecondPart 去:
public int getElementCountOfSecondPart(int lineNumber) {
return lineNumber * 2 + 1;
}
好了, 你已经到头了, 可好像还是找不到对称的影子呀? 前面说"程序的结构反映了问题的结构", 难道这个结论并不总是成立的?
有这么一个故事, 我估计很多人都听说过(文字摘自以下网址 http://www.niwota.com/submsg/5682754/):
有一位牧师在某个星期六的早晨正在为明天的讲道稿大伤脑筋. 他的太太外出买东西了, 外面正下着雨, 小儿子失去了户外活动的机会, 在屋里折腾. 牧师的思路一再被儿子打断.
牧师手边正好有本旧杂志, 为了把儿子从身边支开, 他撕下一张彩色世界地图, 再撕成碎片, 丢到客厅地板上对儿子说: "Johnny, 你把它拼成原样, 我就给你一个 Nickle(25 美分镍币). "
儿子有事可做, 又有报酬可得, 积极性很高, 立刻拼了起来. 牧师想, 这下子我可以安静一个上午, 构思自己的讲道稿了. 谁知道只隔了十分钟, 儿子就来敲书房的门了, 说已经拼好. 牧师不相信, 跑到客厅一看, 果然整幅地图完整无缺. 牧师又懊恼又惊奇地问儿子: "你怎么那么快就拼好了呢? "
儿子得意地说, 这再简单不过了, 这张地图的背后印着一幅人物肖像, 我想, 如果这个人拼对了, 世界地图也就拼对了.
牧师忍不住笑了起来, 很高兴地给了儿子一个镍币, 说, 你替我把明天讲道的题目也准备好了: 如果一个人是对的, 那么这个人的世界也是对的.
现在我们的程序能够输出一个对称的图案来, 肯定不是巧合, 而且我也可以肯定地告诉你, 这里面是有对称的. 你可以再仔细找找看, 如果你已经找到或者实在找不出来, 那么可以往下看了:
现在看来是不是很明显呢? 也许你早也看出来了. 我们能得到有什么启示呢?
运用**直觉(Intuition)**去思考!
如果你的代码中怎么变换也找不出对称来, 当你的人都是错的时候, 你的世界还可能正确吗? 所以你甚至不用费心去上机验证了.
发明了**差分机(difference engine)的计算机先驱查尔斯·巴贝奇(Charles Babbage)**说:
我曾两次被(议员)问到, "巴贝奇先生, 请问假如您往机器里输入了错误的数据, 还会出来正确的答案吗? "我实在无法恰当地理解是怎样的逻辑混乱才会(使他们)提出这样的一个问题.
On two occasions I have been asked [by members of Parliament], ‘Pray, Mr. Babbage, if you put into the machine wrong figures, will the right answers come out?’ I am not able rightly to apprehend the kind of confusion of ideas that could provoke such a question.
看得出来巴贝奇的评论还是很客气的, 他当时似乎在寻求议员拨款来支持他的差分机研究, 我估计他当时内心其实想说: “你丫脑子进水了, 问这种问题!”
巴贝奇谈的是往正确的机器里输入错误的数据的情况, 在这里, 如果连机器里面(即代码)都已经是错的, 那么即便给出了正确输入, 也不可能有正确的输出了.
在某些特殊情况下, 你也许会碰到"负负得正"的情况, 但这不过是巧合而已.
你可能遇到过这样的 bug:
你加了一个新特性, 系统出错了, 你找到一处 bug, 然后你很奇怪, 为何之前居然没问题? 而在你改正这个 bug 后, 之前的一些功能反而不正常了!你可能打死也想不到系统中还有另一个你没发现的 bug 在默默地抵消了它!
诚然, 这样的"负负得正"情况即便能工作也是非常脆弱的.
当事实与直觉不符时, 那么一定有什么地方出错了.
回到我们的问题, 再单独地拿输出空格部分来看:
public int getElementCountOfFirstPart(int lineCount, int lineNumber) {
return lineCount - lineNumber - 1;
}
有对称吗? 它有两个不同变量, 单独的一份随便你怎么去变换, 你都找不到对称. 这也是为何你需要二份一左一右围绕在星号旁边才能形成对称.
关于直觉, 如果你还有兴趣, 可以见我之前写的另一篇文章(有些读者可能已经看过), 深入图解字符集与字符集编码–定长与变长, 也有谈到用天平之类的模型来直观地思考问题.
本质, 证明以及直觉
按前面那图:
如果有人试图从输出的 1, 3, 5, 7 的展开式的对称性来向你证明表达式"lineNumber*2+1"的对称性, 那么呢? 这不过是本末倒置. 正如前面所说, 你把表达式做个变换就可以看出表达式是对称的, 对称是该表达式的本质属性, 所以输出的1, 3, 5, 7 的对称性恰恰是表达式所决定的.
相信很多人都跟作者类似, 在大学的数学课上, 被那些形形色色的恐怖的证明弄得苦不堪言:
这里是在对"人"弹琴, 数学大"牛"们请走开或请无视(要鄙视, 俺也认了), 这里不是在说你们!你们不会懂的!
如果你的老师只能通过证明来告诉你一件事情为什么是这样, 通常你还是很难明白它为什么是这样, 你甚至可以怀疑老师是否真的深刻理解了这件事情, 要么他就是不打算告诉你真正的原因:
好好反思一下你是否在什么事情上得罪了他? 你写作业是不是全靠"Ctrl+C, Ctrl+V"?
又或者他想让你自己去领悟:
真是用心良苦!你体会到了没有? 你领悟了吗? 要是没有请继续, 学费是不会退滴, 你别领悟到其它地方去了~
而如果你的老师可以通过直觉告诉你事情为什么是这样, 你也许就会说: "啊哈, 原来如此(Aha moment)!"从此你就记住了事情为什么是这样了, 那些冗长的证明你都可以丢到一边去了.
独立的数据模型(Isolated Data Model)
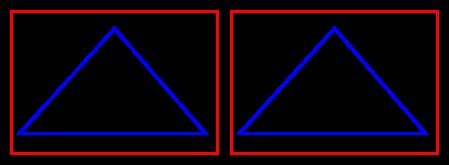
前面说到 getElementCountOfFirstPart 和 getElementCountOfSecondPart 两个方法达到了抽象的极致, 从而与具体的表现形式解耦. 在有了对称性之后, 我们甚至可以反转两个表现形式, 依然可以呈现出所谓的"三角形"出来:
对比两种情况, 不变的是三个部分中的那些数字:
所以这才是图案的"魂", 或者说是它的"意", 抽象出意, 我们就能"得意而忘形".
前面说过也许有一天, 客户的需求可能扩展到 web service 上, 对于一个较大的行数, 需要传输较大的数据, 但有了这种解耦, 我们可以把一个纯粹的数组传递过去:
[3][1][3]
[2][3][2]
[1][5][1]
[0][7][0]
另一方可以在收到这个数据模型后, 再把图形还原.
因为存在对称性, 第三列甚至也可以不传.
灵活性(Flexibility)与松耦合(Loose Couple)
而这个还原过程则可以很灵活地处理, 下图演示了在本地直接利用上述两方法获取图案模式并用 icon 图片展示的效果:
代码如下(我对 swing 之类的编程也不是很熟, 随便在网上搜来的代码改了下):
public class PatternPic extends JPanel {
private static final long serialVersionUID = 1L;
private Image image;
public PatternPic(Image image) {
this.image = image;
};
@Override
public void paintComponent(Graphics g) {
super.paintComponent(g);
int width = image.getWidth(this);
int height = image.getHeight(this);
int lineCount = 4;
Pattern pattern = new Pattern();
for (int lineNumber = 0, y = 0; lineNumber < lineCount; lineNumber++, y += height) {
// 直接获取各部分的数目
int elementCountOfFirst = pattern.getElementCountOfFirstPart(lineCount, lineNumber);
int elementCountOfSecond = pattern.getElementCountOfSecondPart(lineNumber);
for (int i = 0, x = elementCountOfFirst * width; i < elementCountOfSecond; i++, x += width) {
g.drawImage(image, x, y, width, height, this);
}
}
}
public static void main(String[] args) throws IOException {
Image image = ImageIO.read(PatternPic.class.getResource("/logo-git-oschina.png"));
JFrame frame = new JFrame();
frame.add(new PatternPic(image));
frame.setSize(800, 600);
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
frame.setVisible(true);
}
}
所以这样的抽象是有很大好处的, 我们说高层的一些抽象如果觉得啰嗦可以去掉一些(如上述就没作过多的抽象), 但这一层的抽象反而要保留. 我们把它作为公共的 API 提供出去, 调用者就不再受限于那些写死的"空格与星号", 这种灵活性与前面说到的可重用性及可扩展性都是紧密相关的.
MVC
MVC 中重要的一点即是强调模型(M, Model)与视图(V, View)的分离. 所谓的模型即是一种独立于视图的数据, 这与我们抽象出来的数据模型是很相似的.
真正的 MVC 与我们这里的例子间或许还有很大差异, 但在解耦合这一点, 两者是一致.
可以对比下最初的玩具式的代码, 那种情况就是一种 紧耦合(tight couple), 而这里则达到了 松耦合(loose couple) 的目的.
在当下, 常常一方面要处理传统的 web 界面, 另一方面又要处理移动端的界面, 抽取出纯粹的数据模型无疑将带给我们很大方便.
在下一篇将谈谈单元测试的问题.