字符集与编码(三) 定长与变长

☯, 首先, 这并不是图片, 这是一个 Unicode 字符, Yin Yang, 即阴阳符, 码点为 U+262F. 如果你的浏览器无法显示, 可以查看这个链接http://www.fileformat.info/info/unicode/char/262f/index.htm. 这与我们要讨论的主题有何关系呢? 下面我会谈到.

连续式表示带来的分隔难题

计算机的底层表示

在计算机的最底层, 一切都成了 0 和 1, 你也许见过一些极客(Geek)穿着印有一串 0 和 1 的衣服招摇过市, 像是数字化时代的某种图腾.

比如, 这么一串 0001100101101110001111111000…, 如果它来自某个文本文件保存后的结果, 我们如何从这一串的 0 和 1 中重新解码得到一个个的字符呢? 显然你需要把这一串的 0 和 1 分成一段一段的 0 和 1, 在讲述编码是如何分隔之前, 我们先看看自然语言的分隔问题.

自然语言的分隔问题

大家是否意识到, 我们的中文句子里字词之间也是连续的呢? 英文里说 “hello world”, 我们说 “你好世界”, “我们 不 需要 在 中间 加 空格!” 在古代, 句与句之间甚至都没有分开, 那时还没有标点! 所以有了所谓的 断句 问题. 让我们来看一个例子:

民可使由之不可使知之 –出自<<论语 第八章 泰伯篇>>

这么一串十个字要如何去分隔并解释呢?

断法一:

民可使由之, 不可使知之.

解释: 你可以去驱使你的民众, 但不可让他们知道为什么（不要去教他们知识）

评论: 很显然是站在统治阶级立场的一种愚民论调.

断法二:

民可, 使由之；不可, 使知之.

解释: 民众可以做的, 放手让他们去做；不会做的, 教会他们如何去做（又或: 不可以去做的, 让他们明白为何不可以）

评论: 这看来是种不错的主张.

显然, 以上的文字是以某种定长或变长的方式组合在一起的, 但是关于它们如何分隔的信息则被丢弃了, 于是在解释时就存在产生歧义可能了.

如何快速准确分词在中文 NLP 领域还是蛮有挑战的一件事, 当然了, 字符集编码的分隔就简单多了.

编码的分隔

自然语言中我们可以使用空格, 标点来减少歧义的发生. 在计算机里, 一切都数字化了, 包括所谓的空格, 标点之类的分隔符.

老子说"道生一, 一生二, 二生三, 三生万物", 计算机则是"二生万物", 0 和 1 表示了一切.

在空格与标点都被数字化的情况下, 我们在这一串 01 中如何去找出分隔来呢? 显然我们需要外部的约定.

8 位（bit） 一组的 字节 是最基本的一个约定, 也是 文件 的基本单位, 文件就是字节的序列. 字节显然就是最基础的一个分隔依据.

定长(Fixed-length)的解决方案

定长仅表明段与段之间长度相同, 但没说明是多长. 有了字节这一基本单位, 我们就可以说得更具体, 如定长一字节或者定长两字节.

ASCII 编码是最早也是最简单的一种字符编码方案, 使用定长一字节来表示一个字符.

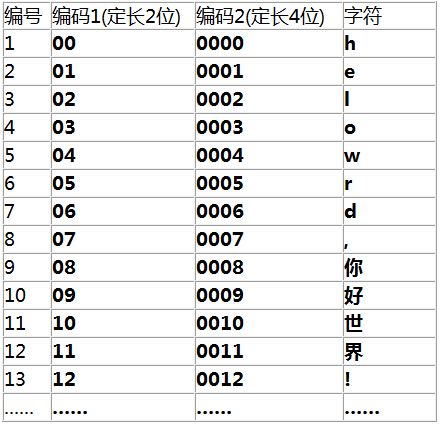
下面我们来看一个具体的编码示例, 为了方便, 采用了十进制, 大家看起来也更直观, 原理与二进制是一样的.

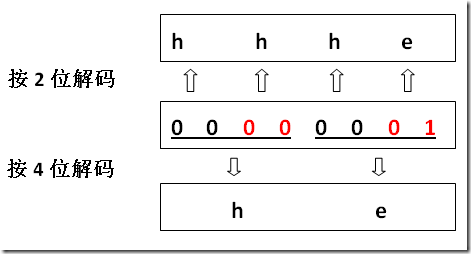
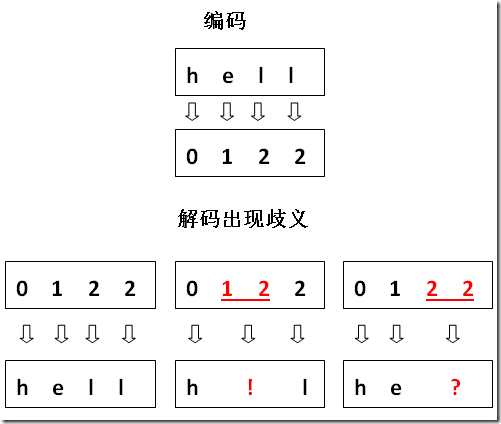
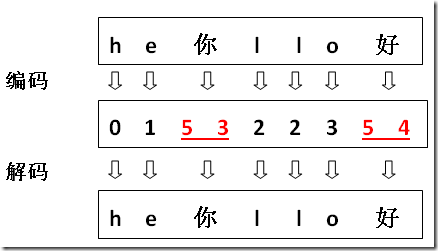
假设我们现在有个文件, 内容是 00000001, 假如定长 2 位（这里的位指十进制的位）是唯一的编码方案, 用它去解码, 就会得到"hhhe"（可以对比图上的编码, 00 代表 h, 所以前 6 个 0 转化成 3 个 h, 后面的 01 则转化成 e, 具体如下图上半部分所示）.

但是, 如果定长 2 位不是唯一的编码方案呢? 如上图中的定长 4 位方案, 如果我们误用定长 4 位去解码, 结果就只能得到"he"（0000 转化为 h, 0001 转化为 e, 具体如上图下半部分所示）!

毕竟, 文件的内容并没*暗示它使用了何种编码! 这就好比孔夫子写下"民可使由之不可使知之"时并没有暗示它是 5|5 分隔（民可使由之|不可使知之）还是 2|3|2|3 分隔（民可|使由之|不可|使知之）那样.

如何区分不同的定长（以及变长）编码方式?

答案是: 你无法区分! 好吧, 这么说可能有点武断, 有人可能会说 BOM(Byte Order Mark 字节顺序标识) 能否算作某种区分手段呢? 但也有很多情况是没有 BOM 的.

关于 BOM, 可见字符集与编码（七）–BOM

总之, 我想给读者传递的一个信息就是:

文本文件 作为一种通用的文件, 在存储时一般都不会带上其所使用编码的信息. 编码信息的丢失, 其实这正是乱码的根源.

我们说无法区分即是基于这一点而言, 但另一方面, 各种编码方案所形成的字节序列也往往带有某种特征, 综合统计学, 语言偏好等因素, 还是有可能 猜测 出正确的编码的, 比如很多浏览器中都有所谓"编码自动检测"的功能.

本章主题主讲定变长, 更多讨论可见乱码探源系列.

定长多字节方案是如何来的?

显然, 字符集的扩充是主要推动力. 定长一字节编码空间撑死了也就 2⁸=256.

这点可怜的空间拿到中国来, 它能编码的汉字量也就小学一年级的水平.

其实 变长 多字节方案更早出现, 比如 GB2312, 采用变长主要为了兼容一字节的ASCII, 汉字则用两字节表示（这也是迫不得已的事, 一字节压根不够用）. 随着计算机在全世界的推广, 各种编码方案都出来了, 彼此之间的转换也带来了诸多的问题. 采用某种统一的标准就势在必行了, 于是乎天上一声霹雳, Unicode 粉墨登场!

前面已经谈到, Unicode 早期是作为 定长两字节 方案出来的. 它的理论编码空间一下达到了 2¹⁶ =65536 (即 64K, 这里 1K=1024=2¹⁰).

对于只用到 ASCII 字符的人来说, 比如老美, 让他们采用 Unicode, 多少还是有些怨言的. 怎么说呢? 比如"he"两个字符, 用 ASCII 只需要保存成 68 65(16 进制), 现在则成了 0068 0065, 前面两个毫无作用的 0 怎么看怎么碍眼, 原来假设是 1KB 的文本文件现在硬生生就要变成 2KB, 1GB 的则变成 2GB!

可是更糟糕的事还在后头, 在老美眼中, 16 位的空间已经算是天量了!要知道一字节里 ASCII 也仅仅用了一半,

后面将会看到, 这一特性为各种变长方案能兼容它提供了很大便利! 因为最高位都是 0.

而且这一半里还有不少控制符. 可随着整理工作的深入, 人们发现, 16 位空间还是不够!!

说起来我们的中文可是字符集里面的大头. “回字有四种写法”, 上大人孔乙己的这句名言想必大家还有点印象. 据说有些新近整理的汉语字典收录的汉字数量已经高达 10 万级别! 我的天! 这里面很多字怕是孔乙己先生也未必认得了!

那现在该咋办呢? 如果还是定长的方案, 眼瞅着就要奔着四字节而去了.

计算机界有动不动就翻倍的优良传统, 比如从 16 位机一下就到 32 位, 32 位一下又到了 64 位. 当然了, 这里面是有各种权衡的, 包括硬件方面的.

那些看到把 68 65 保存成 0068 0065 已经很不爽的人, 现在你却对他们说, “嘿, 伙计, 可能你需要进一步存成 00000068 00000065…”. 容量与效率的矛盾在这时候开始激化.

容量与效率的矛盾

首先, 需要明确一下:

• 所谓 容量, 指用几个字节表示一个字符, 显然用的字节越多, 编码空间越大, 能表示更多不同的字符, 也即容量越大.
• 所谓 效率, 当表示一个字符用的字节越多, 所占用的存储空间也就越大, 换句话说, 存储（乃至检索）的效率降低了.

如果说效率是 阴, 那么容量就是 阳. （我没还没忘记自小学语文老师就开始教导的, 写作文要遥相呼应）

我们说定长不是问题, 关键是定几位. 定少了不够用, 定多了太浪费. 定得恰到好处? 可怎样才算恰好呢? 你可能会说, 至少要能容纳所有字符吧? 但重要的事实是并非所有的字符所有的人都用得上! 哪怕用得上, 也可能是偶尔用上, 多数时候还是用不上!

<<动物庄园>> 里说: 所有动物生而平等, 但有的动物比其它动物更平等!

字符之间并不是平等的. 用数学的语言来说, 每个字符出现的机率不是等概率的, 但表示它们却用了同样长度的字节.

学过<<数据结构与算法>>的同学可能听过哈夫曼编码(Huffman Coding), 又称霍夫曼编码, 就为了解决这样的问题.

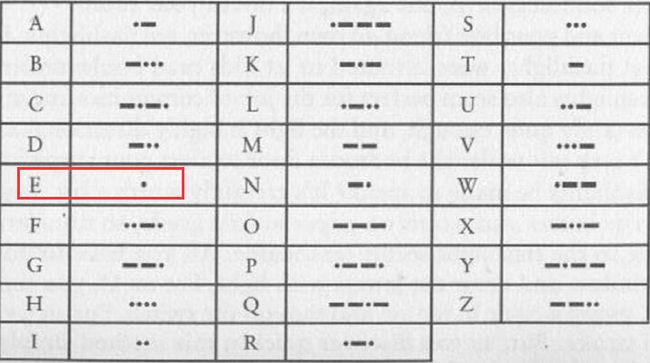
如果你对前一篇所发的莫尔斯电码图还有印象, 你就会发现, 字母 e 只用了一个 点（dot） 来编码.

其它字母可能觉得不公平, 为啥我们就要录入那么多个 点 和 划（dash） 才行呢? 这里面其实是有统计规律支撑的. e 出现的概率是最大的. z 你能想到什么?

zoo 大概很多人能想到, 厉害一点可能还能想到 zebra（斑马）, Zuckerberg（扎克伯格）, 别翻字典! 你还能想到更多不?

但含有的 e 的单词则多了去了. zebra 中不就有个 e 吗, Zuckerberg 中还两个 e 呢!

在存储图片时, 一个像素点用几个位来表示也是一个很值得考究的问题. 你也许听过所谓的 24 位真彩色, 这暗示了一个像素使用了高达 3 个字节来表示. 24 位的空间可以表示高达 1600 多万种颜色, 但各种颜色的出现概率在均衡度上肯定要好于字符.

回到我们的主题, 虽然很多字连我们的孔乙己先生见了都要摇头, 可还是有少部分人会用到它们, 比如一些研究古汉字的学者. 有些人取名还喜欢弄些偏僻字, 所以很多人口登记方面的系统也有这个超大字符集的需求.

好吧, 我们不能不顾这些人需求. 那么有可能在 定长方案 的框架下解决这一 容量与效率的矛盾 吗? 答案是 否定的!

矛盾是事物发展的动力, 下面我们将看到定长方案的简单性使它无法缓和容量与效率的冲突, 平衡这一对矛盾的努力最终推动了编码方案从定长演变到变长, 事情也由此从简单变得复杂了.

CAP 理论及扩展

CAP 是什么玩意?

著名的 Brewer 猜想说: 对于现代分布式应用系统来说, 数据一致性(Consistency), 系统可用性(Availability), 服务规模可分区性(Partitioning)三个目标(合称 CAP)不可同时满足, 最多只能选择两个.

你可能要问, 这貌似跟我们要讨论的问题风牛马不相及? 别着急, 我们可以借鉴他的这种思想, 扩展到我们的问题上来.

两个维度

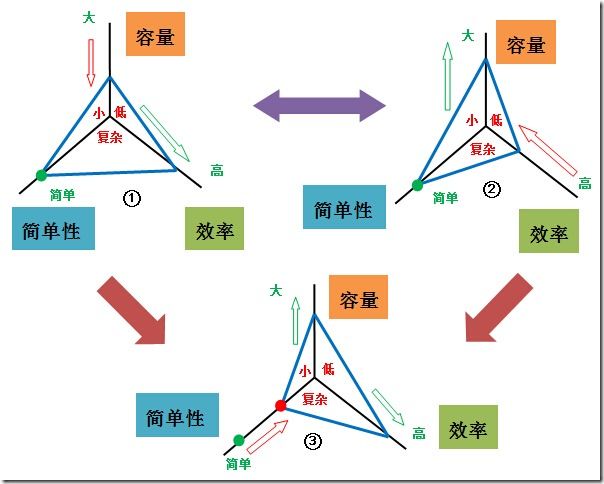
我们所应对的问题常常很抽象, 有时借助某些 隐喻（metaphor） 可以帮助我们来理解. 天平就是一个很好的隐喻.

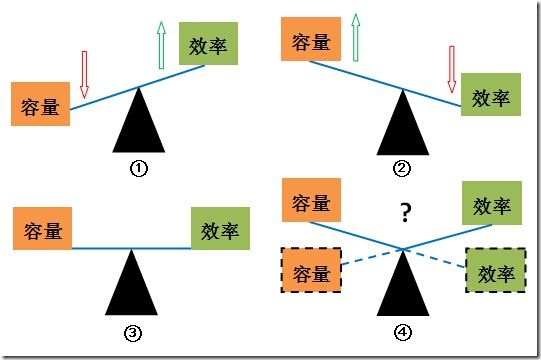
先看图中四个天平. 你叫它跷跷板我也没意见, 反正我没打算吃美术这碗饭!（嗯, 也许是少个了指针的缘故, 希望这空指针的天平不要引发什么异常. ）

这幅图表示的就是定长方案下容量与效率的一种约束关系.

1. 容量小则效率高
2. 容量大则效率低
3. 容量与效率均不能让人满意!
4. 容量与效率均较好, 但这是不可能的情形!

让我们具体解释一下: 天平的蓝色横梁一种刚性约束的隐喻. 所谓刚性, 这里简单理解成不能变形就是了.

天平的两端的容量与效率是它的两个维度, 或者说两个自由度. 不必去纠结物理学上的定义, 简单理解就是它们能自由上下就好了. 但我们可以看到, 由于受到横梁的约束, 两个维度同时向上是不可能的! 它们的相互运动呈现出彼消此长的关系.

天平可以隐喻很多, 比如安全性与便利性. 为什么要我录入验证码? 为什么支付宝登录与支付要用不一样的密码? 为何输入密码还不够, 还要什么手机验证码? 这些都很不方便呀!

当你觉得只有一个前门还不够方便时你又加开了个后门, 但你是否想过在方便自己的同时也方便了小偷呢?

鱼和熊掌不可兼得!

三个维度

好了, 现在要再次拓展一个维度了, 以使得它更像 CAP 理论.

还有一个维度在哪呢? 我们说容量大是好, 效率高是好, 我们为何青睐定长方案呢? 因为定长它简单, 简单当然也是好, 复杂就不好了. 这就是第三个维度–简单性.

你也可以叫成复杂性, 意思是一样的.

先深呼吸一下, 让我们再看一个图:

首先这里多了一个维度, 天平模型不足以表达了, 改用三条互成 120 度的直线表示这三个维度. 越往里, 红色的字代表是越差的情况；越往外, 绿色的字代表是越好的情况.

图中的约束在哪呢? 就在蓝色的三角形上, 它有一个固定的周长, 这就代表了它的约束. 也许我们把它想像成一条首尾相接的固定长度的 钢丝绳 更好, 在图中它只是被拉成了三角形. 它可以在三个维度上运动, 这让它比天平的横梁更灵活, 但它的长度不能被拉伸, 它不是橡皮绳!!

这幅图能告诉我们什么?

• 图1跟图2, 当我们维持简单性不变时, 容量与效率的关系其实跟天平模型中是相似的, 也是一种彼消此长的关系.
• 图3, 让简单性下降（换句话说就是变复杂了）, 才能为其它两个维度腾出"余量"来. 即是说你要"牺牲"简单性来调和容量与效率的矛盾.

我们能从模型得到什么启示呢?

一, 事物的多个方面往往是相互制衡的.

在前面的图中, 我们用钢丝绳来形象隐喻这种制衡, 深刻理解制衡是各种直觉与预见性的前提, 当我们作出决定时, 便能够预判出可能的后果. 深层次的矛盾暗示了我们有些冲突是不可避免的, 同时为我们找到正确解决问题的路径指明了方向.

二, 制衡的局面暗示了凡事有代价, 站在一个全局上去考量, 我们常常需要在各方面达成某种平衡与妥协.

举个例子, 分层会对性能有所损害, 但不分层又会带来紧耦合的问题. 很多时候, 架构就是关于平衡的艺术. 如果我们能明白这一点, 就不会为无法找到"完美"方案而苦恼.

三, 复杂性从根本上是由需求所决定的. 我们既要求容量大, 又要求效率高, 这种要求本身就不简单, 因此也无法简单地解决.

你功能做好了, 用户说性能还不行；

你性能达标了, 用户说界面还太丑. . .

丫的能不能先把首付款付清了再跟哥提要求? !

为什么谈这些理论?

一方面我不想仅仅为谈定变长而只谈定变长, 单纯谈理论又往往过于抽象. 我想说的一点是"我们在编码上所遇到的困境往往不过是我们在软件开发过程中遇到的各种困境的一个缩影".

下图是所谓的 芒德布罗集（**Mandelbrot set）, 是 分形（Fractal） 理论中的一个重要概念. 图片来自 wiki 百科.

很多问题需要我们站在更高层面上去观察与思考时才能发现它们的某些相似性或者说共性, 这些共性被抽象出来也就形成了我们的理论.

不识庐山真面目, 只缘身在此山中. –苏轼<<题西林壁>>

另一方面, 因为这种相似性, 我们在编码问题上得到的启示也能够指导我们去解决其它领域的问题. 我想这就是这些理论的意义所在.

调和矛盾的努力, 兼容考虑与变长方案的引入

通过前面分析, 我们知道, 定长两字节方案无法满足容量增长, 转向定长四字节又会引发效率危机, 最终, Unicode 编码方案演化成了变长的 UTF-16 编码方案. 那么UTF-8 方案又是如何来的呢? 为何不能统一成一个方案呢? 搞这么多学起来真头痛!

我们前面提到了有一群 ASCII 死忠对 Unicode 统一使用两字节编码 ASCII 字符始终是有不满的, 现在眼见简单的定长方案也不行了, 他们中的一些大牛终于忍无可忍. 既然决定抛弃定长, 他们决定变得更彻底, 于是这帮人揭竿而起, 捣鼓出了能与 ASCII 兼容的 UTF-8 方案. （_注: 真实历史也许并非如此, 我不是考据癖, 以上叙述大家悠着看就是了, 别太当真. _）

如今装个逼还分高低格, 大牛不折腾, 谁又知道他们是大牛呢? 只是可怜了我们这些码农, 你还在苦苦研究 sql, 忽如一夜春风来, Nosql 菊花朵朵开.

UTF-16 用所谓的 代理对(surrogate pair) 来编码 U+FFFF 以上的字符. 在采用了变长之后, 事情变得复杂了, 以后我们还将继续探讨 代理区, 代理对, 编码单元(Code Unit) 等一系列由此而来的概念.

这种变化甚至还影响到对 字符串长度 的定义, 比如, 在 java 中, 你可能认为包含一个字符的字符串它的长度就是 1, 但现在, 一个字符它的长度也可能是 2! 这样的字符也无法用 char 来存储了.

UTF-8 因为能兼容 ASCII 而受到广泛欢迎, 但在保存中文方面, 要用 3 个字节, 有的甚至要 4 个字节, 所以在保存中文方面效率并不算太好, 与此相对, GB2312, GBK 之类用两字节保存中文字符效率上会更高, 同时它们也都兼容 ASCII, 所以在中英混合的情况下还是比 UTF-8 要好, 但在国际化方面及可扩展空间上则不如 UTF-8 了.

其实 GBK 之后又还有 GB18030 标准, 采用了 1, 2, 4 字节变长方案, 把 Unicode 字符也收录了进来. GB18030 其实是国家强制性标准, 但感觉推广并不是很给力.

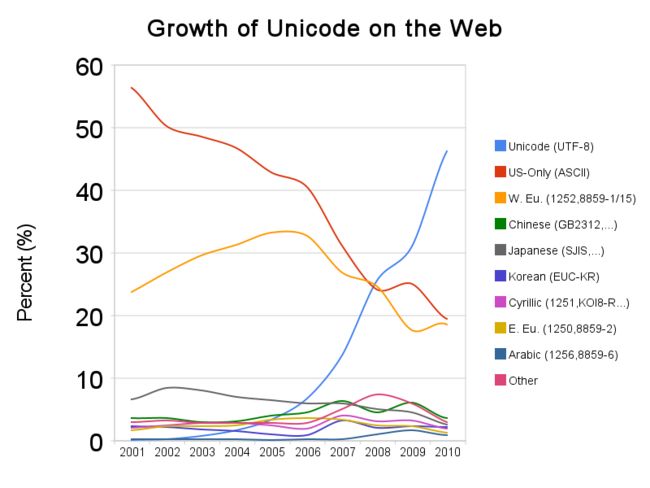
目前, UTF-8 方案在越来越多的地方有成为一种默认的编码选择的趋势. 下面是一张来自 wiki 百科的图片, 反映了 UTF-8 在 web 上的增长.

在软件开发的各个环节强制统一采用 UTF-8 编码, 依旧是避免乱码问题的最有效措施, 没有之一. 技术人员也许更偏爱技术问题技术解决, 但不得不承认有时行政手段更加高效!

变长(Variable-length)的编码方案

好了, 现在是时候谈谈变长方案的实现问题了, 在这里将通过尝试自己设计来探讨这一问题.

变长设计的核心问题自然就是如何区分不同的变长字节, 只有这样才能在解码时不发生歧义.

利用高位作区分

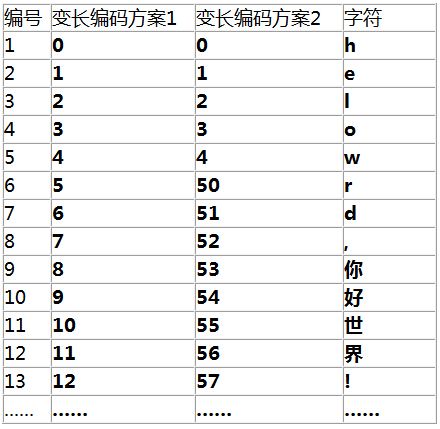
还是以前面的例子来看, 我们设计了几种变长方案

第一种方案的想法很美好, 它试图跟随编号来自然增长, 它还是可以编码的, 但在解码时则遇到了困难. 让我们来看看.

可见, 由于低位的码位被"榨干"了, 导致单个位与多位间无法区分, 所以这种方案是行不通的.

第二种方案, 低位空间有所保留, 5 及以上的就不使用了. 然后我们通过引入一条变长解码规则:

从左向右扫描, 读到 5 以下数字按单个位解码；读到 5 或以上数字时, 把当前数字及下一个数字两位一起读上来解码.

让我们来看个实例

这种方案避免了歧义, 因此是可行的方案, 但这还是非常粗糙的设计, 如果我们想在这串字符中搜索"o"这个字符, 它的编码是 3, 这样在匹配时也会匹配上 53 中的 3, 这种设计会让我们在实现匹配算法时困难重重. 我们可以在跟随位上也完全舍弃低位的编码, 比如以 55, 56, 57, 58, 59, 65, 66…这样的形式, 但这样也会损失更多的有效编码位.

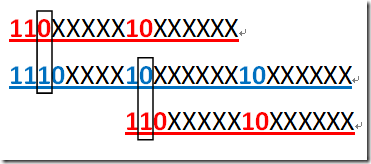
GB2312, GBK, UTF-8 的基本思想也是如此. 下面也简单示例一下（0, 1 代表固定值；黑色的 X 代表可以为 0 或 1, 为有效编码位）:

注: GBK 第二字节最高位也可能为 0.

其实关键就在于用高位保留位来做区分, 缺点就是有效编码空间少了, 可以看到三字节的 UTF-8 方式中实际有效的编码空间只剩两字节. 但这是变长方案无法避免的.

我们还可以看到, 由于最高位不同, 多字节中不会包含一字节的模式. 对于 UTF-8 而言, 二字节的模式也不会包含在三字节模式中, 也不会在四字节中；三字节模式也不会在四字节模式中, 这样就解决上面所说的搜索匹配难题. 你可以先想想看为什么, 下面的图以二, 三字节为例说明了为什么.

可以看到, 由于固定位上的 0 和 1 的差别, 使得二字节既不会与三字节的前两字节相同, 也不会它的后两字节相同. 其它几种情况原理也是如此.

利用代理区作区分

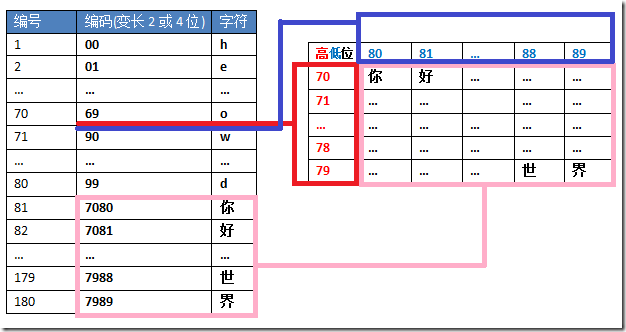
让我们再来看另一种变长方案. 用所谓代理区来实现.

这里挖出 70-89 间的码位, 形成横竖 10×10 的编码空间, 使得能再扩展 100 个编码空间. 原来 2 位 100 个空间损失了 20 还剩 80, 再加上因此而增加的 100 个空间, 总共是 180 个空间. 这样一种变长方式也就是 UTF-16 所采用的, 具体的实现我们留待后面再详述.

好了, 关于定变长的问题, 就讲到这里, 下一篇将继续探讨前面提及但还未深入分析的一些问题.