汉诺塔问题——分治思想

汉诺塔规则如下：

1、有三根相邻的柱子，标号为x,y,z。

2、x柱子上从下到上按金字塔状叠放着n个不同大小的圆盘。

3、现在把所有盘子一个一个移动到柱子z上，并且每次移动同一根柱子上都不能出现大盘子在小盘子上方。

目录：

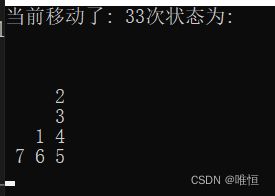
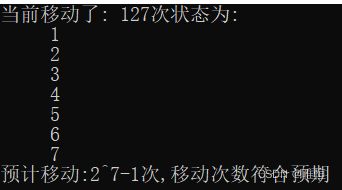
1.代码效果预览

2.分治思想剖析汉诺塔原理

3.汉诺塔常见疑惑剖析

4.代码及其解析，关于头部代码的理解误区

1.代码效果预览

 

2.分治思想剖析汉诺塔原理

首先汉诺塔可以分为两种情况，1层和n层。

一层就直接将盘子从x移到z,不在多做解释。

那么n层怎么解决呢？

首先明确我们的目的是什么？

把x上的盘子全部移到到z上面，且不能让大的压在小的上面。

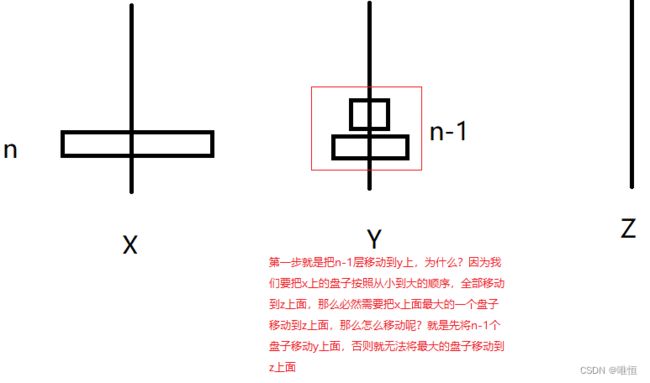
那么第一步是什么？

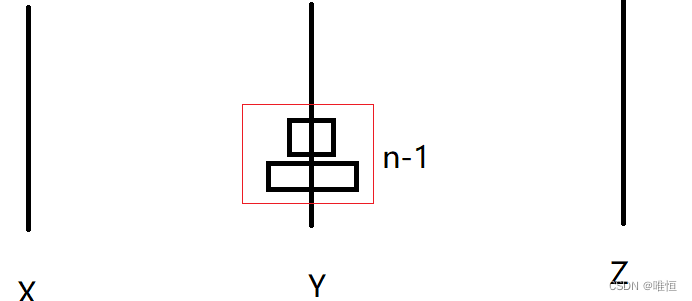
 那么怎么移动这n-1层呢？

这个先不管，假设现在我们已经成功移动了这n-1层。

那么接下就是将第n层移动到z上面。

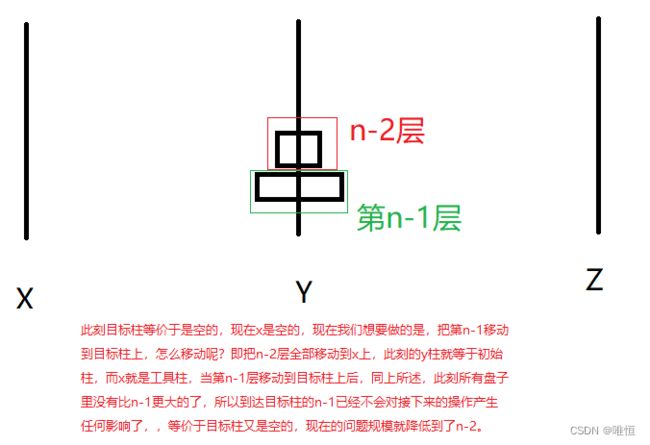
 好了这里已经成将第n层移动到z上了，那么我们回顾一下规则，不能将大盘子压在小盘子上面，现在我们引入一个概念，目标柱，工具柱，初始柱。

刚开始时盘子全部在x上面，那么x即为初始柱，此时我们希望将盘子全部移动到z上面，那么z即为目标柱，而在此过程中，我们借助了y,则y即为工具柱。

当最大的盘子移动到目标柱时，我们不管移动任何盘子到目标柱，都不会犯规了，因为，没有任何盘子大于它，不存在将大盘子压在小盘子上面的说法，因为它就是最大的。

所以此刻，我们可以等价看作，目标柱是空的，问题的规模从n降阶为了n-1,因为那个最大的盘子已经对接下来的操作产生不了任何影响了。

即如图：

 

 

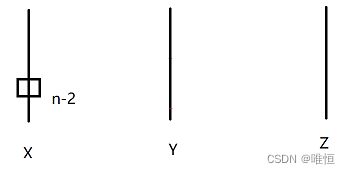
好了，现在的状况是不是感觉有些相似？

那么现在我们要做什么呢？

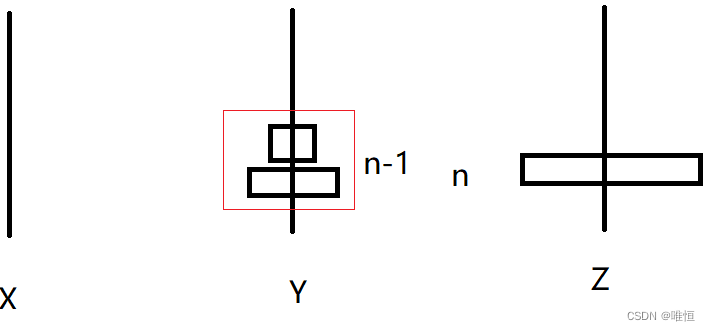
 当完成上述操作后，状态如图：

 那么接下来就如同回到了初始状态，对比一下最开始的状态。

 

是不是除了问题规模减小了之外，没有任何区别？

这就是分治法的思想，将规模很大的问题，分割成为一个个类似的小的子问题。

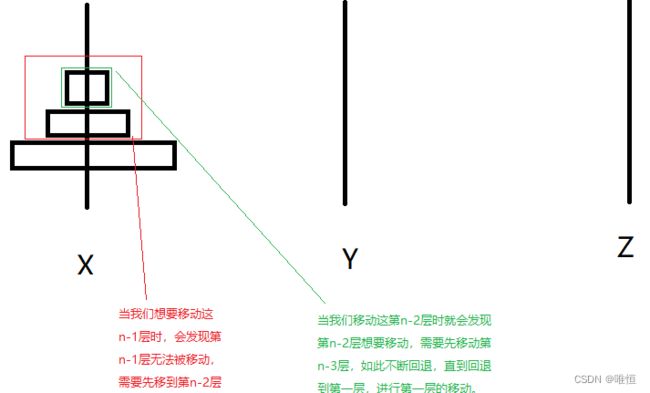
好了理解了原理之后，我们回到刚开始遗留的问题上面，我们要把第n层移动到目标柱上面，就要先把，第n-1层全部先移到工具柱上面。

那么这n-1层是如何移动的呢？

 

3.汉诺塔常见疑惑剖析

我们在将前n-m层移动到工具柱的这整个过程中，还剩下m层的初始柱起到了什么作用，充当了什么角色？

当我们在移动这n-m层时，初始柱剩下的这m层都是最大的，前面的n-m层里面并没有比这m层的柱子里面任意一层盘子大的，所以可以等价于这个初始柱是空的，就像前面所讲的将第n层移动到目标柱后，这个第n层不会再对后续操作产生任何影响，所以可以把此时的目标柱看作是空的一样，是同一个道理。所以在这个过程中，可以把这个不会产生影响的初始柱当作，空的工具柱来使用。

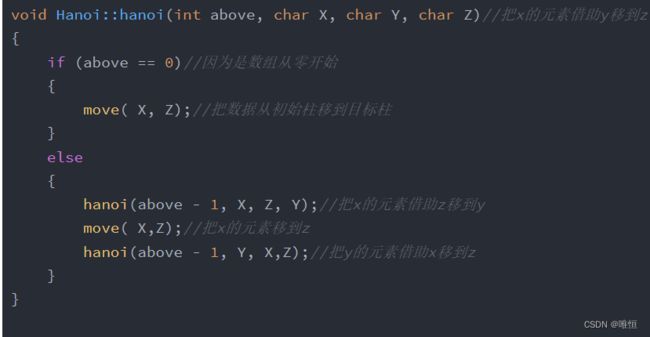
4.代码及其解析，关于头部代码的理解误区

解析不动，代码先行。

/****************************************************
    > File Name:     Hanoi
    > Author:        唯恒
    > Mail:          [email protected]
    > Created Time:  2022年10月24日
*******************************************************/

#include 
#include
#include
using namespace std;

class Hanoi {
public:
    const int number;//汉诺塔层数
    char **pillar;//模拟xyz三个柱子
    void visit();//观看三个柱子
    int find_top(int row);//查找当前列的顶部不为空格的元素的层数
    void move(char X, char Z);//将顶部元素从x柱移到z柱
    void hanoi(int above, char X, char Y, char Z);//圆盘从x借助y移到z
    Hanoi(int number);//构建对象时确定汉诺塔的个数
};

Hanoi::Hanoi(int numbers):number(numbers)
{
    //为柱子分配内存
    pillar = new char*[number];

    for (int i = 0;i < number;i++)
    {
        pillar[i] = new char[3];
    }

    //将三个柱子初始化
    for (int i = 0;i < number;i++)
    {
        for (int j = 0;j < 3;j++)
        {
            if (j == 0)//如果是0号柱子则初始化为1,2,3,4,......
            {
                pillar[i][0] = '1' + i;
            }
            else//否则初始化为空格
            {
                pillar[i][j] =' ';
            } 
        } 
    }
    visit();//初始化汉诺塔后查验一下
}

void Hanoi::visit()
{
    static int count = 0;//记录下移动了几次
    cout << "当前移动了: "< 9)
    {
        cout << "请输入汉诺塔的层数(数量请勿超过9，否则难以显示):";//不能超过9是因为,每个柱子输出时，间隔一个空格
        cin >> n;                                                 //二位数，会导致数字连着不利于观看,并且我定义的                                   
    }                                                             //是字符数组，只有1—9的ASCII,二位数没有ASCII
     Hanoi h(n);
    h.hanoi(n-1, 'X', 'Y', 'Z');
    return 0;
}

其它部分的代码，注释已经很清晰了，便不在多做解释，这里只讲解，最主要的部分。

关于头部代码的理解误区： 

当above==0时，每次都是把，X的数据移动到Z上面，那么岂不是会把大的盘子全部压在小的上面？而且Y去哪里了？怎么没有用到Y?

注意这里的XYZ是char类型；那么举个例子：

当汉诺塔为两层时：

第一步：进入程序hanoi(1,X,Y,Z);（传1的原因是这里的柱子是数组，下标从0开始）

第二步：above!=0，进入hanoi（0,X,Z,Y）;

第三步：above==0，进入注意了，第二步时传入的是此时第三步里的Z,实际上等于柱子Y。

主代码解析：

1

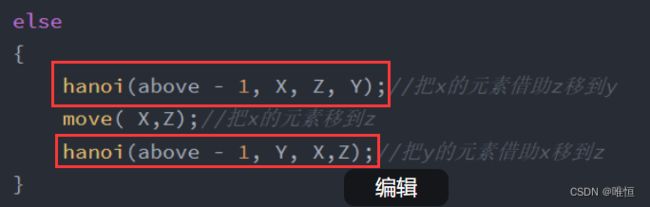
当above==0，便不作解释了，当above！=0时

这一步即为，将above-1层全部移动到Z上。

即前面的这幅图：

 2.

这一步即为将x上最大的那个盘子移动到目标柱上。

即前面的这幅图：

 3.

 即前面的这幅图：

4.当前面的

 hanoi（）内部的递归执行情况，便类似于前面的这幅图：

如果还是没有理解，也没有关系，后续我会在b站上传该代码的讲解视频，并在下方附上链接。