文章解读与仿真程序复现思路——电网技术EI\CSCD\北大核心《基于外部性理论的网侧储能成本疏导机制研究》
这个标题涉及到一个关于储能的研究,主要聚焦在基于外部性理论的网侧(电网侧)储能成本疏导机制上。
-
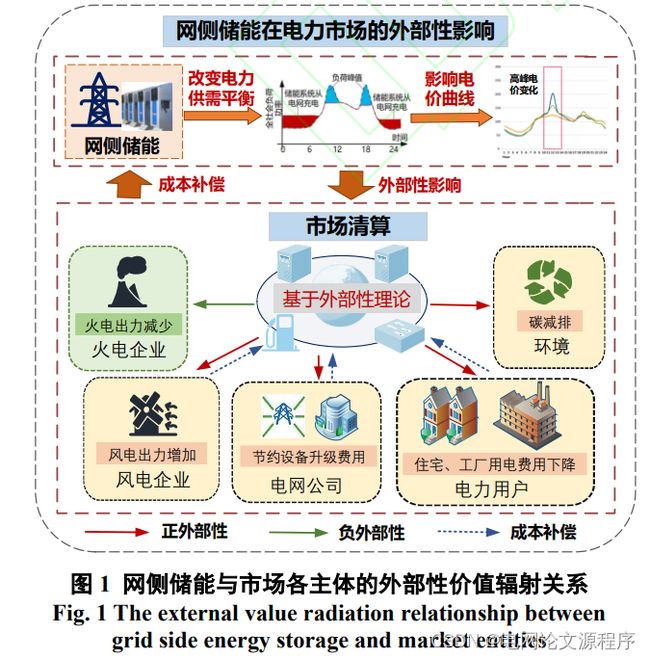
基于外部性理论: 这表明研究的框架或者理论基础是"外部性理论"。外部性是指某个经济活动的影响不仅限于直接参与者,还波及到其他与之无直接关系的人或者企业。在储能领域,外部性理论可能用于分析储能系统对电网整体效益的影响,包括降低网络传输损耗、提高系统韧性等。
-
网侧储能: 网侧意味着储能系统位于电力网络的一侧,这通常涉及到与电力系统相连接的储能设备。这可能包括储能电站、电池系统等,旨在提供电力网络服务。
-
成本疏导机制: 这指的是一种机制或者方法,其目的是引导、调整或者管理储能的成本。在这个背景下,"成本疏导"可能涉及到通过一定的机制来优化或者调整储能系统的运营和成本结构,以更好地适应电力系统的需求。
因此,整个标题的含义可以解读为,研究的焦点是通过应用外部性理论,探索在电网侧的储能系统中,如何设计一种成本疏导机制,以优化储能系统的运营,提高整个电力系统的效益。这可能涉及到经济、技术和政策等多个方面的考虑。
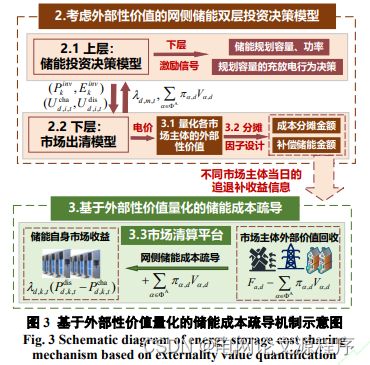
摘要:“双碳”目标下构建以新能源发电为主体的新型电力系统需要大量灵活性资源保障其可靠运行。大规模的网侧储能为电力系统提供调峰、调频、惯量支撑等多元服务,具有重要调节作用。然而,网侧储能仅靠峰谷电价差获取电量收益难以回收其投建成本,已成为制约大规模网侧储能发展的主要原因。为此,基于外部性理论对网侧储能成本疏导机制展开研究。在分析市场环境下网侧储能对源-网-荷多主体外部性价值特点的基础上,建立包含储能外部性价值量化及储能成本疏导的网侧储能双层规划决策模型,即上层给出储能的规划容量,下层模拟网侧储能参与现货市场运营对市场电价的影响,并量化其对不同市场主体的外部性价值,同时反馈到上层决策模型引导储能投资;进而设计网侧储能的成本分摊方法及基于市场清算的成本疏导机制。算例结果表明所提方法能够指导网侧储能的投建规模,所设计的成本疏导机制满足多市场主体激励相容,可以缩短储能项目的成本回收年限,并与现有电力市场交易规则兼容性好。
这段摘要描述了在实施"双碳"目标的背景下,建设以新能源发电为主体的新型电力系统所需的灵活性资源。特别强调了大规模的网侧储能在电力系统中提供调峰、调频、惯量支撑等多元服务的关键作用。然而,摘要也指出,目前网侧储能主要依赖于峰谷电价差来获取电量收益,这难以完全回收其投建成本,成为制约其大规模发展的主要障碍。
为解决这一问题,研究者基于外部性理论展开了对网侧储能成本疏导机制的研究。在分析市场环境下,研究考虑了网侧储能对整个电力系统(源-网-荷)的多主体外部性价值特点。为此,建立了一个双层规划决策模型,上层确定了储能的规划容量,而下层则模拟了网侧储能参与现货市场运营对市场电价的影响,并量化了其对不同市场主体的外部性价值。这些信息反馈到上层决策模型,从而引导储能投资。
进一步,研究者设计了网侧储能的成本分摊方法,并提出了基于市场清算的成本疏导机制。通过案例研究,结果表明这种方法可以有效地指导网侧储能的投建规模,而设计的成本疏导机制不仅满足多市场主体的激励要求,还可以缩短储能项目的成本回收年限。此外,该机制与现有电力市场交易规则兼容性良好。
总体而言,这项研究提供了一种理论框架和方法,有助于优化网侧储能的规划、投资和运营,以更好地支持新型电力系统的可靠运行和可持续发展。
关键词:网侧储能 外部性价值双层规址分摊因子:成本疏导机制:
-
网侧储能 (Grid-Side Energy Storage):
- 解读 : 指的是在电力系统中,储能系统安装在电网侧(网侧),用于储存电能以供电力系统调度和优化。这些系统可以在需要时释放储存的电能,以平衡电力系统的供需。
-
外部性价值 (Externalities):
- 解读 : 外部性是指一种经济活动对非参与者产生的影响,这些影响可能是正面的(正外部性)或负面的(负外部性)。在这里,可能是指储能系统对整个电力系统及其参与者产生的额外价值或影响。
-
双层规划 (Two-Tier Planning):
- 解读: 双层规划通常指的是将一个大的规划问题分解为两个层次,其中上层处理高层次的决策,而下层则处理更详细的问题。在这里,可能指的是一个包含上层和下层决策的规划模型,用于优化储能系统的规模和运营。
-
成本分摊因子 (Cost Allocation Factor):
- 解读: 成本分摊因子是一种指标,用于确定各个参与者应对某项成本负担的程度。在这里,可能是指确定储能系统建设和运营成本如何分摊给不同的市场主体或参与者。
-
成本疏导机制 (Cost Guidance Mechanism):
- 解读 : 成本疏导机制是一种引导或指导系统中各项成本的方法。在这里,可能指的是一种机制,通过它可以引导储能系统的建设和运营成本,以更好地满足市场需求和提供经济效益。
综合来看,摘要中提到的关键词涵盖了从网侧储能的规划到运营的多个方面,包括外部性价值的考虑、双层规划的决策模型、成本分摊和成本疏导机制等。这些概念在设计和优化储能系统,特别是在新能源发电主导的电力系统中,都是至关重要的。
仿真算例:算例包含 5 个火电商、2 个风电商和 1 个网侧储能运营商,风电出力的预测值选取中国西北某风电场实际数据,储能和火电的相关参数见表 1 所示。本文建立的双层决策模型在 MATLAB R2022a 中使用YALMIP 优化工具箱的 CPLEX 求解器进行迭代求解。为了验证本文所提的储能成本疏导机制有效性,设计了如表 2 所示的三个对比场景:1)S1(基准场景),节点边际电价(LMP)机制下无储能参与的场景;2)S2(传统场景),节点边际电价(LMP)机制下仅考虑总运行成本最低的储能决策场景;3)S3(验证场景),节点边际电价(LMP)机制下同时考虑系统总成本和储能外部性价值补偿的储能决策场景,即本文所提方法的验证场景。
仿真程序复现思路:这个案例涉及建立双层决策模型,以验证储能成本疏导机制的有效性。为了简化说明,以下是伪代码示例,演示可能的复现思路:
% 步骤 1: 准备数据
% 假设数据已经准备好,例如储能和火电的参数,风电出力预测等
% 步骤 2: 构建双层决策模型
% 使用 YALMIP 工具箱,构建双层决策模型,并指定 CPLEX 作为求解器
clear all;
clc;
% 假设有关数据的一些变量,这里的数据是示例数据,实际使用时需要替换为真实数据
wind_power_forecast = rand(24, 1) * 100; % 风电出力预测
% 其他数据...
% YALMIP 设置
yalmip('clear');
ops = sdpsettings('solver', 'cplex', 'verbose', 1);
% 定义变量
% 假设有关决策变量的一些定义,需要根据实际情况进行调整
energy_storage_decision = sdpvar(1, 1); % 储能决策变量
% 其他变量的定义...
% 构建上层目标函数和约束
upper_level_objective = ... % 根据实际情况定义上层优化目标
upper_level_constraints = ... % 根据实际情况定义上层优化约束
% 构建下层目标函数和约束
lower_level_objective = ... % 根据实际情况定义下层优化目标
lower_level_constraints = ... % 根据实际情况定义下层优化约束
% 构建双层决策模型
upper_level_problem = optimize(upper_level_constraints, upper_level_objective, ops);
lower_level_problem = optimize([lower_level_constraints, energy_storage_decision >= 0], lower_level_objective, ops);
% 步骤 3: 设计对比场景
% 设置三个不同的场景(S1,S2,S3),对应不同的储能决策情景
% 省略对比场景的设置,根据实际需要进行设计
% 步骤 4: 仿真求解
% 在每个场景下进行仿真求解
for each scenario in [S1, S2, S3]
% 根据场景设置不同的目标函数和约束
% 求解上层问题
upper_level_problem = optimize(upper_level_constraints, upper_level_objective, ops);
% 获取上层问题的结果
upper_level_decision = value(energy_storage_decision);
% 将上层决策传递给下层问题
lower_level_constraints = [lower_level_constraints, energy_storage_decision == upper_level_decision];
% 求解下层问题
lower_level_problem = optimize([lower_level_constraints, energy_storage_decision >= 0], lower_level_objective, ops);
% 提取并记录结果
upper_level_cost = value(upper_level_objective);
lower_level_cost = value(lower_level_objective);
% 输出或记录结果
fprintf('Scenario: %s, Upper Level Cost: %f, Lower Level Cost: %f\n', scenario, upper_level_cost, lower_level_cost);
end
% 步骤 5: 结果分析和对比
% 比较三个场景下的仿真结果,对储能成本疏导机制的有效性进行分析和评估
% 省略分析过程,根据实际需要进行设计