Motion Plan之基于采样的路径规划算法笔记

Motion Plan之搜索算法笔记

背景：

基于采样算法是一种在路径规划中广泛应用的有效方法。它通过在图中随机选择点来生成一个简化的搜索图，从而加速搜索过程。这种方法的主要优点包括减少内存使用，避免计算错误，具有动态障碍物对抗性，以及易于应用于高维C空间。
基于采样路径规划优缺点如下：
优点：
a.即时生成搜索图不需要存全部图信息、减少内存
b.不试图明确构造C空间及其边界
c.即时生图有一定动态障碍物对抗性
d.易于应用于高维C空间
e.如果进行了足够的预处理，支持快速查询
不足：
a.需要解决2点边界值问题。
b.对某些任务效果不佳。
b.1.不太可能在狭窄通道中放置样本节点。
b.2.在约束表面上采样/连接节点困难。
c.既不是最优的也不是完整的。

1.有了图搜索路径规划为什么还需要随机采样路径规划"

Sample base plan"和"搜索路径规划"是两种不同的策略，它们在处理问题和优化解决方案时有所不同。
** a.Sample base plan**：这是一种基于样本的规划方法，它通过生成大量的样本点来寻找最优解。这种方法的优点是可以处理高维度和复杂的问题，因为它不需要对整个问题空间进行详细的搜索。然而，这种方法的缺点是可能会产生次优的解决方案，因为它并不总是能找到全局最优解⁴。此外，如果样本点的生成和选择方法不合适，可能会导致效率低下⁵。
** b.搜索路径规划**：这是一种基于搜索的规划方法，它通过在问题空间中搜索最优路径来找到解决方案。这种方法的优点是在给定足够的计算资源和时间的情况下，可以找到全局最优解。然而，这种方法的缺点是在处理高维度和复杂的问题时，可能会遇到"维度灾难"的问题，因为问题空间的大小随着维度的增加而指数级增长，这使得搜索变得非常困难和耗时。
这两种方法各有优缺点，适用于不同的问题和场景。在实际应用中，可能需要根据具体的问题特性和需求，选择最合适的规划方法。对于一些特别复杂或者高维度的问题，可能需要结合使用这两种方法，或者使用其他的优化策略和技术。

2.基于采样路径规划算法主要围绕以下几点，衍生出各种随机采样路径规划算法

a.如何采样撒点(采样撒点方式）：均匀采样、高斯采样、随机采样
采样方法是选择节点的具体方式，常见的采样方法包括均匀采样、随机采样、高斯采样等。均匀采样是从图中均匀分布的点中随机选择点，随机采样是从图中随机选择点。
b.何时建图（何时做采样点是否可行点判断）
建图时机是指确定在何时生成搜索图。通常情况下，当需要搜索解决方案时，可以生成搜索图。但是，在问题规模较大时，生成搜索图可能会消耗大量时间和内存。因此，可以根据问题的具体情况来确定建图的时机。
c.建图范围（需要遍历的采样点）
建图范围是指需要遍历的采样点。通常情况下，建图范围包括图中所有节点。但是，在问题规模较大时，遍历所有节点可能会消耗大量时间和内存。因此，可以根据问题的具体情况来确定建图范围。
可行的路径规划方法：概率路线图 (PRM)，快速探索随机树 (RRT)；最优路径规划方法：RRT*；加速收敛：RRT#，Informed-RRT*，和 GuILD。

3.基于采样的路径规划算法的共同处理流程：

尽管这些算法在实现细节上有所不同，但它们都遵循了基于采样的路径规划算法的基本框架，即采样、构建图或树、碰撞检测和路径搜索。这些共同的处理流程使得这些算法能够在各种复杂的环境中进行有效的路径规划。具体选择哪种算法，需要根据实际应用的需求和环境条件来决定。
基于采样的路径规划算法的共同处理流程主要包括以下几个步骤
** a.采样**：在配置空间中随机撒点，生成一组采样点。
** b.构建图或树**：根据采样点之间的关系（例如距离、连通性等），构建一个图或树来表示整个配置空间。
** c.碰撞检测**：检查采样点和采样点之间的连线是否与障碍物发生碰撞，如果有碰撞，则舍弃这些采样点或连线。
** d.路径搜索**：在构建的图或树上搜索一条从起点到终点的路径。
这个流程是基于采样的路径规划算法的基本框架，不同的算法可能会在这个基础上添加一些额外的步骤，例如概率路图算法（PRM）的学习阶段和查询阶段，快速随机扩展树算法（RRT）的树扩展过程，RRT*算法的路径优化过程等。这些算法的具体实现和优化方法可能会有所不同，但它们的核心思想都是通过采样和搜索来寻找一条满足特定条件的路径。

4.prm、rrt、rrt*、rrt# 、Informed-RRT* 、GuILD差异

基于采样的路径规划算法，如概率路线图（PRM）、快速搜索随机树（RRT）、RRT_、RRT#、Informed-RRT_和GuILD，虽然在实现细节上有所不同，但它们都遵循了一些共同的处理流程，包括采样、构建图或树、碰撞检测和路径搜索。这些共同的处理流程构成了这类算法的基本框架。
然而，这些算法在具体实现这些处理流程时，会有一些重要的差异。主要差异:

1. PRM属于多查询算法,可用于离线全局规划;RRT属于单查询算法,适用于在线规划。
2. PRM采用批量全局采样;RRT采用增量式采样。PRM覆盖整个空间,RRT增量扩展。
3. PRM构建无向图(可能有环),RRT构建有向树。
4. PRM全局在图上搜索路径,RRT从根节点增量搜索。
5. RRT*、Informed-RRT*、GuILD在RRT基础上引入了贪心策略、启发式、预构建路线图等机制进行加速和优化。

更详细的介绍他们之间差异:

1. 采样范围:全局vs增量
   • PRM:预处理阶段进行全局批量采样
   • RRT/RRT_/_:增量迭代采样
   • GuILD:在增量迭代采样的基础上结合全局Roadmap
2. 数据表示:图vs树
   • PRM:构建路线图(图结构)
   • RRT/RRT#:构建树结构
   • RRG/GuILD:既有树结构,也结合路线图
3. 搜索策略:全局vs增量
   • PRM:全局搜索路径
   • RRT/RRT*/RRT#:增量构建搜索树
   • GuILD:在RRT的搜索树上结合全局路线图搜索
4. 是否利用额外信息进行加速和优化
   • RRT*/RRT#:在RRT上增加贪心策略
   • Informed-RRT*:集成启发式采样
   • GuILD:集成局部子集采样
5. 时间性能

• PRM:两阶段分离,预处理时间长
• RRT系列算法:适合在线规划

下面是这些算法的原理和流程的详细描述：
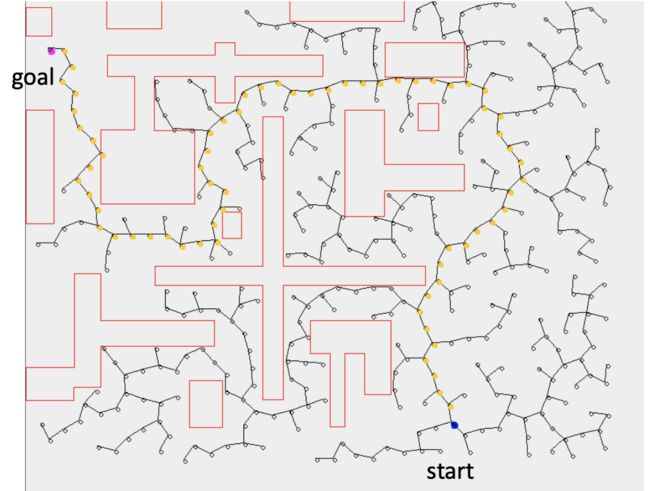
PRM(Probabilistic Roadmap Method):

1. 原理:通过在自由空间中随机采样节点,然后使用本地规划方法连接这些节点来构建路线图(roadmap)。
2. 流程:分学习阶段和查询阶段。学习阶段中,随机采样自由空间中的配置,并使用简单的运动规划器测试这些配置之间的连接;通过重复这个过程,逐步构建路线图。查询阶段中,将起点和终点连接到路线图,然后在路线图上搜索路径。
   • 采样：在整个配置空间中进行均匀采样，生成一些节点。
   • 连接：对于每个节点，找到距离它最近的几个节点，并检查它们之间是否可以直接连接。如果可以，就在这两个节点之间添加一条边。
   • 搜索：在这个图中，使用图搜索算法（如Dijkstra或A*）来找到从起始点到目标点的最短路径。

• 缺点是环境变化后要重新构建地图,计算代价大，难以处理窄通道。

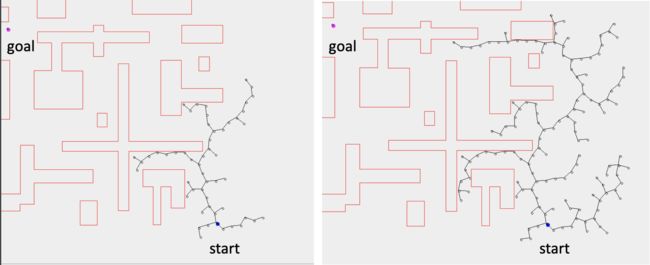
RRT(Rapidly Exploring Random Tree):

1. 原理:一种增量搜索算法,通过扩展一棵树来探索空间。从起点开始,选择最靠近树的随机配置并尝试扩展树向该配置移动来增长树。
2. 流程:重复采样、找到nearest节点、尝试连接新样本和nearest节点、如果连接成功则添加新节点和边到树中,直到树达到目标区域或指定迭代次数。
   • 采样：在每次迭代中，随机采样一个点。
   • 连接：找到距离这个点最近的树中的节点，然后向这个点的方向扩展一条边。
   • 搜索：重复上述过程，直到找到一条从起始点到目标点的路径。

• 缺点是扩展方向随机,扩展不均匀,易进入死胡同。

RRT*(Rapidly Exploring Random Tree*):

1. 原理:RRT的优化版本。与RRT类似,但在扩展树的同时,还会改进树上已经存在的路径,通过重新连接节点来优化路径质量。
2. 流程:与RRT基本相同,增加了考虑近邻节点代价的ChooseParent过程和Rewire过程。
   • 采样：与RRT算法相同，每次迭代中随机采样一个点。
   • 连接：不仅连接到距离采样点最近的节点，还会尝试连接到周围的其他节点，以寻找可能的更优路径。
   • 搜索：与RRT算法相同，通过不断迭代来搜索路径。

• 缺点是重新连接代价较大，收敛到最优解较慢。

RRT# (Rapidly-exploring Random Tree Sharp)：

1. 原理:这是RRT*的一个变种，它在每次迭代中都会尝试优化整个树，以更快地找到更优的路径⁴。

Informed-RRT:*

1. 原理:利用先验信息来加速RRT*的搜索过程。会向更有可能包含最优解的区域扩展树。在找到初始解决方案后，它会在一个椭圆区域内进行采样，该区域包含了所有可能改进当前解决方案的状态。
2. 流程:与RRT*基本相同,改进了采样策略,偏向先验设置的有利区域采样。

GuILD:

1. 原理:利用prebuilt roadmap来加速RRT的搜索过程。首先构建全局roadmap,然后使用RRT在roadmap上执行局部搜索以查找解决方案路径。它依赖于增量密集化来发现逐渐缩短的路径。在计算出从起始点到目标点的可行路径后，GuILD利用这些信息从Informed Set的局部子集进行采样。
2. 流程:分为Global Planning和Local Planning两个阶段。Global Planning构建roadmap覆盖整个空间;Local Planning基于roadmap使用RRT搜索路径。
   

正文：

概率路线图（PRM）规划器

概率路线图规划器是一种运动规划算法，确定从机器人的起始配置到目标配置的路径，同时避免碰撞。PRM背后的基本思想是从机器人的配置空间中随机取样，测试它们是否在自由空间中，并使用本地规划器尝试将这些配置连接到其他附近的配置。
概率路线图规划器包括两个阶段：构造阶段和查询阶段。

• 在构造阶段，构建一个路线图（图）。创建一个随机配置。它连接到邻居，例如，最近的k个。
• 在查询阶段，将起始配置和目标配置连接到图上，然后通过Dijkstra的最短路径查询获得路径。

概念和符号定义：

• 路线图是一个图G(V,E)
• Q-Free中的机器人配置q是一个顶点
• 边(q1, q2)意味着这些机器人配置之间的无碰撞路径 - 这里需要本地规划器
• 需要一个度量来衡量配置之间的距离：dist(q1,q2)（例如，欧几里得距离）
• 使用节点的粗采样和边的细采样
• 无碰撞的顶点，边在Q-Free中形成一个路线图
  

PRM路线图构建

• 最初的空路线图图G
• 随机选择一个机器人配置q
• 如果q→Q-Free（无碰撞配置）则添加到G
• 重复直到选择N个顶点
• 对于每个顶点q，选择k个最近的邻居
• 本地规划器尝试将q连接到邻居q’
• 如果连接成功（即，无碰撞的本地路径），添加边(q, q’)

带有障碍物的二维平面环境

在C-空间中随机采样N个无碰撞的配置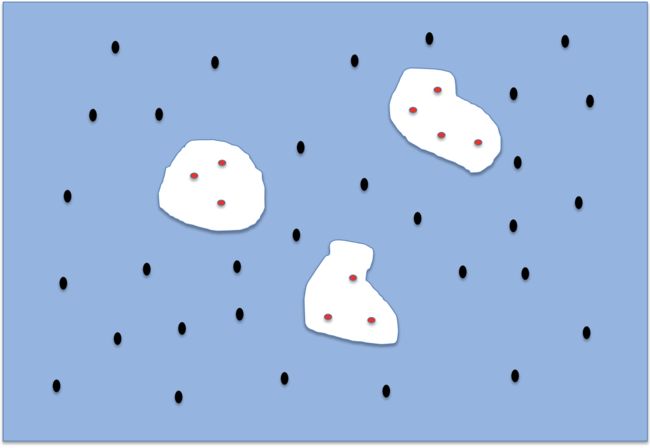

将Q-Free中的每个顶点与K个最近的邻居连接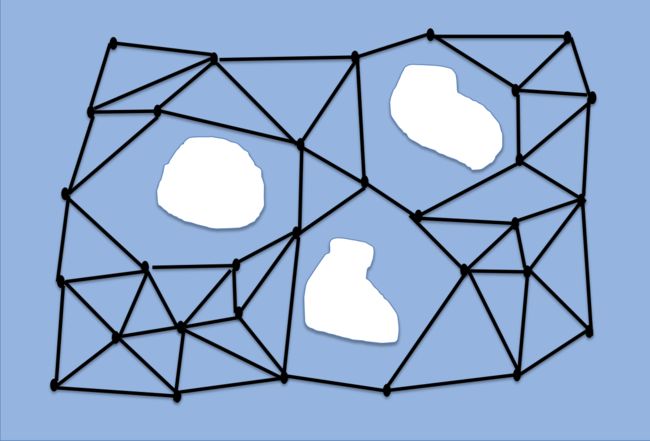

#roadmap construction algorithm
input:
  n: number of nodes in the roadmap
  k: number of closest neighbors to examine for each configuration
output:
  A roadmap g = (v, e)
--------------------------------------------------------------------------
v <-- 0
e <-- 0
while |v| < n do
    repeat
        q<--random configuration in Q
    until q is collision-free
    v <--v U v{g}
end while
for all q in V do
    Nq <--the k closest neighbors of q chosen from V according to dist
    for all q' in Nq do
        if (q,q') not in E and delta(q,q') npt null then
            E <--E U{(q,q')}
        end of
    end for 
end for 

PRM搜索路径

• 给定q_init和q_goal，需要将每个连接到路线图
• 在路线图中找到q_init和q_goal的k个最近邻居，规划本地路径
• 问题：路线图图可能有断开的组件…
• 需要找到从q_init，q_goal到同一组件的连接
• 一旦在路线图上，使用Dijkstra算法

将起点和终点连接到路线图中的最近节点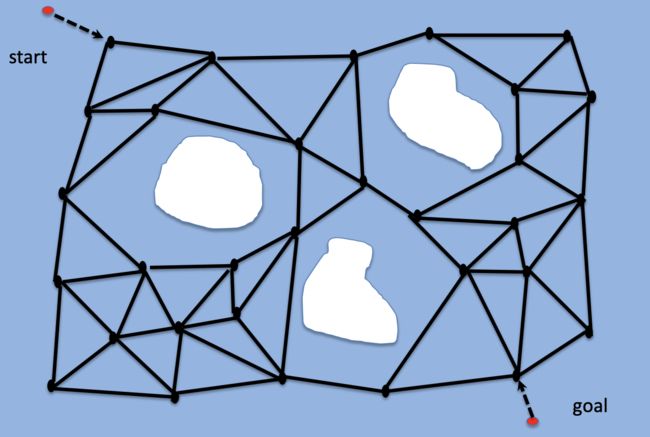

图搜索最短路径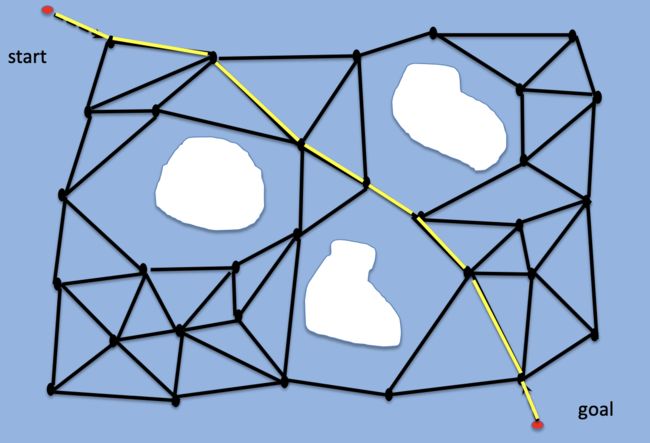

处理多个查询-一旦在路线图上，就找到一条路径

#solve query algorithm
input:
    qinit:the initial configuration
    qgoal:the goal configuration
    k:the number of closest neighbors to examne for each configuration
    g=(v,e):the road map computed by roadmap construction algorithm
output:
    a path from qinit to qgoal or failure
--------------------------------------------------------------------------
Nqinit<--the k closest neighbors of qinit from V according to dist
Ngoal<--the k closest neghbors of qgoal from V according to dist
V<--{qinit} U{qgoal} U V
set q' to be the closest neighbor of qinit in Nqinit
repeat
    if delta(qinit,q') not null hen
       E<--(qinit,q') U E
    else
       set q' to be the next closest neighbor of qinit in Nqinit
    end if
until a connection was succesful or the set Nqinit is empty
set q' to be the closest neighbor of qgoal in Nqgoal
repeat
    if delta(qgoal,q') not null hen
       E<--(qgoal,q') U E
    else
       set q' to be the next closest neighbor of qgoal in Ngoal
    end if
until a connection was succesful or the set Ngoal is empty
P<--shortest path(qinit,qgoal,G)
if P is not empty then
    return p
else
    return failure
end if

懒惰的碰撞检查：

• 在不考虑碰撞的情况下采样点并生成线段（懒惰）。
• 在未进行碰撞检查的路线图上找到一条路径。
• 如果路径不是无碰撞的，则删除相应的边和节点。
• 重新开始寻找路径。
  

RRT：快速探索随机树

• 单查询规划器用于从配置A到配置B
• 随机采样Q-Free以从q_start到q_goal的路径，向目标生长一棵树
• 可以使用2棵树，分别以q_start和q_goal为根。
• 随着树的生长，它们最终会共享一个公共节点，并合并成一条路径
  

RRT：构建树算法

通过执行随机控制在树中生成“下一个状态”，从起点到终点构建一棵树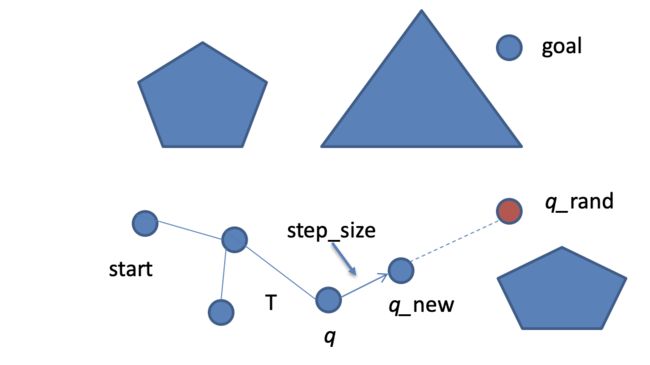

• 起始节点是树的根
• 生成新的随机配置q_rand
• 找到最近的树节点q
• 沿着路径(q, q_rand)移动距离step_size
• 如果无碰撞，将q_new添加为新的树节点
• 重复以上步骤…

• 从起始节点开始，一次扩展一节点的树
• 每次随机生成新的样本配置
• 尝试将样本连接到树中的最近节点
• 如果无碰撞，向样本方向创建新节点的小距离（步长） - 这里需要调用本地规划器

• 一旦树达到目标，我们就有了一条路径
• 路径在任何意义上都不是最优的
• 每次路径可能都会不同 - 随机的
• 可以扩展到更高的维度

#build rrt algorithm
input:
    q0:the confguration where the tree is rooted
    n:the number of attempts to expand the tree
output:
    A tree  T=(V,E)that is rooted at q0 and has<=n confgurations
----------------------------------------------------------------------
V<-{q0}
E<--0
for i=1 to n do
    qrand<--a randomly chosen free confguration
    extend RRT(T,qrand)
end for
return T

#extend rrt algorith 
input:
    T=(V,E):an RRT
    q:a configuration toward which the treet T is grown
output:
    a new confguration qnew toward q,or nil in case of failure
----------------------------------------------------------------------
qnear<--closest neighbor q of T
qnew<--progress qnew by step size along the straght line in Q between qnew
qrand
if qnew is collision free then
    V<--V U (qnew)
    E<--E U {(qnear,qnew){
    return qnew
end if
return nil

优点 l 易于实现 l 旨在找到从起点到终点的路径 l 比PRM更具目标导向性
缺点 l 不是最优解 l 不高效（留有改进空间） l 在整个空间中取样

最优RRT（RRT∗）

RRT（快速探索随机树）是一种增量式的、基于采样的运动规划算法，它构建了一棵树，这棵树以起始位置为根，不断向未探索的区域扩展。然而，RRT生成的路径并不一定是最优的。
为了解决这个问题，研究人员提出了RRT算法。RRT 在RRT基础上做了改进，主要是进行了重新选择父节点和重布线的操作。试想在RRT中，我们的采样点最终与整棵树上和它最近的点连了起来，但这未必是最好的选择，我们的最终目的是让这个点与起点的距离尽可能近。RRT* 便对此做了改进，它在采样点加入路径树以后，以其为圆心画了一个小圈，考虑是否有更好的父节点，连到那些节点上能使起点到该点的距离更短（尽管那些节点并不是离采样点最近的点）。
在介绍RRT之前我们先介绍RRG算法，之所以介绍RRG是因为RRG引入了RRT中非常重要的技术点：父节点重连技术。所以我们先来看看RRG，然后在切入RRT会更容易理解RRT算法。

快速探索随机图（RRG）：

快速探索随机图算法被引入为一种增量（而非批处理）算法，用于构建可能包含循环的连接路线图。RRG算法与RRT类似，首先尝试将最近的节点连接到新的样本。如果连接尝试成功，新节点将被添加到顶点集。然而，RRG有以下不同之处。每次向顶点集V添加新点xnew时，都会尝试从V中所有其他在半径r(card (V )) = min{γRRG(log(card (V ))/ card (V ))1/d, η}的球内的顶点进行连接，其中η是出现在局部转向函数定义中的常数，γRRG > γ∗ RRG = 2 (1 + 1/d) 1/d (µ(Xfree)/ζd) 1/d。对于每个成功的连接，都会向边集E添加一个新的边。因此，很明显，对于相同的采样序列，RRT图（一个有向树）是RRG图（一个无向图，可能包含循环）的子图。特别是，这两个图共享相同的顶点集，RRT图的边集是RRG图的边集的子集。
还可以考虑另一个版本的算法，称为k-nearest RRG，其中寻找k个最近邻的连接，k = k(card (V )) := kRRG log(card (V ))，其中kRRG > k ∗ RRG = e (1 + 1/d)，并且Xnear ← kNearest(G = (V, E), xnew, kRRG log(card (V )))，在算法5的第7行。
注意，k ∗ RRG是一个只依赖于d的常数，不依赖于问题实例，不像γ ∗ RRG。此外，kRRG = 2e对所有问题实例都是有效的选择。

Algorithm : RRG
V ← {xinit}; E ← ∅;
for i = 1, . . . , n do
    xrand ← SampleFreei;
    xnearest ← Nearest(G = (V, E), xrand);
    xnew ← Steer(xnearest, xrand) ;
    if ObtacleFree(xnearest, xnew) then
        Xnear ← Near(G = (V, E), xnew, min{γRRG(log(card (V ))/ card (V ))1/d, η}) ;
        V ← V ∪ {xnew}; E ← E ∪ {(xnearest, xnew),(xnew, xnearest)} ;
        foreach xnear ∈ Xnear do
            if CollisionFree(xnear, xnew) then E ← E ∪ {(xnear, xnew),(xnew, xnear)}
return G = (V, E);

最优RRT（RRT∗）：

维护树结构而不是图结构不仅在内存需求方面更经济，而且在某些应用中可能更有优势，例如，相对容易地扩展到具有微分约束的运动规划问题，或应对建模错误。RRT∗算法通过修改RRG，避免形成循环，通过移除“冗余”边，即不是从树的根（即初始状态）到顶点的最短路径的部分，从而获得。由于RRT和RRT∗图是具有相同根和顶点集的有向树，边集是RRG的子集，这相当于对RRT树进行“重连”，确保顶点通过最小成本路径到达。
在讨论算法之前，需要引入一些新的函数。给定两点x1, x2 ∈ R^d，让Line(x1, x2) : [0, s] → X表示从x1到x2的直线路径。给定一棵树G = (V, E)，让Parent : V → V是一个函数，它将一个顶点v ∈ V映射到唯一的顶点u ∈ V，使得(u, v) ∈ E。按照惯例，如果v0 ∈ V是G的根顶点，那么Parent(v0) = v0。最后，让Cost : V → R≥0是一个函数，它将一个顶点v ∈ V映射到从树的根到v的唯一路径的成本。为了简化，在陈述算法时，我们将假设一个加法成本函数，即Cost(v) = Cost(Parent(v)) + c(Line(Parent(v), v))，尽管在下一节的分析中这并不是必需的。按照惯例，如果v0 ∈ V是G的根顶点，那么Cost(v0) = 0。
RRT∗算法，如算法伪代码所示，以与RRT和RRG相同的方式将点添加到顶点集V。它还考虑了从新顶点xnew到Xnear的连接，即，其他在距离r(card (V )) = min{γRRT∗ (log(card (V ))/ card (V ))1/d, η}内的顶点。然而，并非所有可行的连接都会导致新的边被插入到边集E。特别是，（i）从Xnear中可以连接到xnew的顶点创建一条边，并且（ii）如果通过xnew的路径的成本低于通过当前父节点的路径的成本，则从xnew到Xnear的顶点创建新的边；在这种情况下，将删除连接顶点和其当前父节点的边，以保持树结构。
还可以考虑另一个版本的算法，称为k-nearest RRT∗，其中寻找k个最近邻的连接，k(card (V )) = kRRG log(card (V ))，并且Xnear ← kNearest(G = (V, E), xnew, kRRG log(i))，在算法6的第7行。

考虑历史成本而不仅仅是局部信息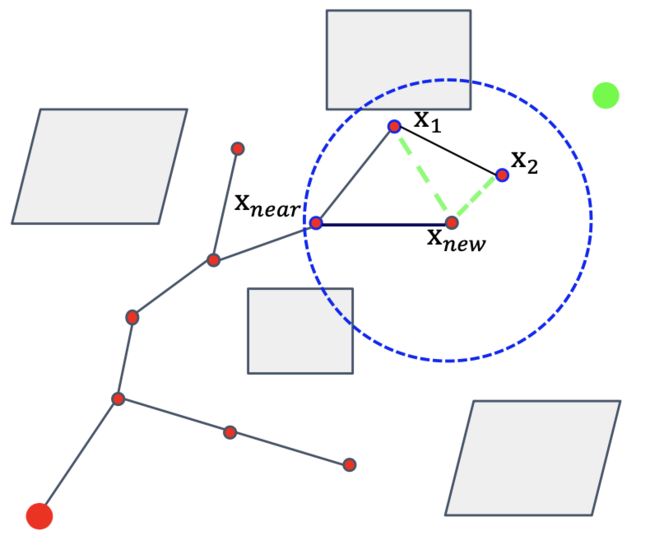

重连以提高局部最优性

Algorithm : RRT∗
V ← {xinit}; E ← ∅;
for i = 1, . . . , n do
    xrand ← SampleFreei;
    xnearest ← Nearest(G = (V, E), xrand);
    xnew ← Steer(xnearest, xrand) ;
    if ObtacleFree(xnearest, xnew) then
        Xnear ← Near(G = (V, E), xnew, min{γRRT∗ (log(card (V ))/ card (V ))1/d, η}) ;
        V ← V ∪ {xnew};
        xmin ← xnearest; cmin ← Cost(xnearest) + c(Line(xnearest, xnew));
        foreach xnear ∈ Xnear do // Connect along a minimum-cost path
            if CollisionFree(xnear, xnew) ∧ Cost(xnear) + c(Line(xnear, xnew)) < cmin then
                xmin ← xnear; cmin ← Cost(xnear) + c(Line(xnear, xnew))
            E ← E ∪ {(xmin, xnew)};
        foreach xnear ∈ Xnear do // Rewire the tree
             CollisionFree(xnew, xnear) ∧ Cost(xnew) + c(Line(xnew, xnear)) < Cost(xnear)
            then xparent ← Parent(xnear);
            E ← (E \ {(xparent, xnear)}) ∪ {(xnew, xnear)}
return G = (V, E);

从经验上看，对于低维规划，我们可以将常数范围设置得稍大于转向距离。
RRT*常用提效优化方法：

• 偏向采样 向目标偏向的采样
• 样本拒绝 拒绝 g + h > c* 的样本
• 分支定界（树剪枝） 剪除非有希望的子树以减少邻居查询成本。
• 图稀疏化 通过分辨率拒绝样本。引入近似最优性。
• 邻居查询 k-最近或范围内最近；近似最近邻；不同维度的范围树。
• 延迟碰撞检查 按潜在的成本值对邻居进行排序。 按顺序检查碰撞，并在找到无碰撞的边时停止。
• 双向搜索
• 有条件的重连 在找到第一个解决方案之前进行重连。
• 数据重用 存储 ChooseParent 和 Rewire 的碰撞检查结果（仅对对称成本有效）。

RRT#

RRT*的利用存在一些缺陷。过度利用的情况下，没有必要对非有前途的顶点进行“重连”。在利用不足的情况下，“重连”只在新节点添加到生成树后发生，并且只对其“附近”的节点起作用。它并不能保证在任何中间迭代中的临时路径是最优的。一言概之：RRT#引入了代价函数、边成本、代价成本、启发函数来记录历史选择路径的代价状态，所以在做新节点选择时候，可以基于这些代价函数快速选出有价值的节点扩展。同时把RRG图探索和利用两阶段做法，解决了RRT算法探索、利用耦合导致的只能求解局部最优问题。既保证了算法渐进最优有保证计算的效率。

摘要

RRT#(RRT “sharp”)，它不仅保证了渐进最优性，而且还确保了以初始状态为根的生成树包含了有可能成为最优解的顶点的最低成本路径信息。这意味着，如果当前图中已经有一些顶点在目标区域内，那么最好的可能解决方案就可以立即计算出来。
为了克服与搜索高维空间相关的计算复杂性，大多数运动规划算法的设计方式相似，并执行两个基本任务：探索和利用。探索获取搜索空间拓扑的信息，即空间的子集如何连接，而利用则通过处理探索任务计算的可用信息逐步改进解决方案。因此，如果可用信息不足，探索可能无法找到解决方案。然而，探索最大程度地利用了当前可用的信息。一般来说，这两个任务的结合方式产生了在次优性、渐进最优性、收敛速率等方面具有不同特性的规划器。为了设计最优的运动规划算法，必须确保探索覆盖整个搜索空间（至少是渐进的），并且利用在不陷入局部解的情况下找到最好的可能解决方案。
概率方法已被证明对于解决具有动态约束的高维搜索空间的运动规划问题非常有效。其中，快速探索随机树(RRTs)是最受欢迎的。然而，最近的研究表明，当算法收敛时，RRTs返回的最佳路径几乎总是（即，以概率1）远离最优解。这重新激发了开发具有最优性保证的增量采样算法来解决运动规划问题的兴趣。在中，作者提出了快速探索随机图(RRG)算法，该算法是渐进最优的，即，它确保当样本数量趋于无穷大时，将找到最优路径。基于RRG算法，同样的作者后来提出了一种新的算法，即RRT*，该算法从RRG算法构造的图中提取一棵树。RRT_算法遵循与RRG算法中的探索过程相同的过程，然而，此外，新的可用信息会立即被利用。这是通过在新采样点的局部区域重新布线树来改进邻居顶点的到达成本值来实现的。因此，探索和利用任务在RRT_算法中是通过设计耦合的，即，当前树的任何顶点的到达成本值都不能在不将新顶点包含到树中的情况下得到改进。由于这两个任务在本质上是不同的，因此，一种直观的提高性能的方法（例如，提高收敛速率）是将这两者分开，并将它们作为不同的过程实现，以便尽可能地并行运行。
RRT#算法将探索和利用作为两个独立的过程实现。为了进一步提高效率，我们在利用步骤中也使用了松弛法。采用了RRG算法的探索算法，然后使用了高斯-赛德尔类型的松弛方法进行利用。RRT#算法保证了渐进最优性，但是，此外，它还确保在每一步，到那一步为止的可用信息都被充分地利用到了最大程度。为底层图构造了一个以初始点为根的生成树，该树包含了从初始点到目标集的最佳可能路径的信息，以及一组顶点的到达成本值，包括有可能成为最优解的目标集。这有两个好处。首先，它确保在每个时间点，算法返回给定当前可用采样点的最短路径。其次，它允许我们根据顶点可能成为最优路径的潜力对顶点进行分类。因此，人们可以快速地确定最有可能找到最优解的区域。这些信息可以随后用来提高算法的收敛速度，以及更有效地探索无障碍空间。

II. 问题的形式化

A. 符号和定义
让X表示状态空间，我们假设它是Rd的一个开子集，其中d ∈ N且d ≥ 2。让障碍区域和目标区域分别由Xobs和Xgoal表示。无障碍空间由Xfree = X \Xobs定义。让初始状态由xinit ∈ Xfree表示。给定两点x, x’ ∈ Rd之间的直线段由Line(x, x’) = {θ ∈ R, 0 ≤ θ ≤ 1 : θx +(1 − θ)x’}表示。让G = (V, E)表示一个图，其中V和E ⊆ V ×V分别是顶点和边的有限集。在后续，我们将使用图来表示从Xfree随机选择的一组（有限）点之间的连接。
后继顶点：给定有向图G = (V, E)中的一个顶点v ∈ V，集值函数succ : (G, v) 7 → V ′ ⊆ V返回可以从顶点v到达的V中的顶点。
前驱顶点：给定有向图G = (V, E)中的一个顶点v ∈ V，集值函数pred : (G, v) 7 → V ′ ⊆ V返回是进入v的边的尾部的V中的顶点。
父顶点：给定有向图G = (V, E)和一个顶点v ∈ V，函数parent : v 7 → u返回一个唯一的顶点u ∈ V，使得(u, v) ∈ E且u ∈ pred(G, v)。
生成树：给定有向图G = (V, E)，G的生成树可以定义为T = (Vs, Es)，其中Vs = V和Es = {(u, v) : (u, v) ∈ E且parent(v) = u}。
边成本值：给定边e = (u, v) ∈ E，函数c : e 7 → r返回一个非负实数。然后c(u, v)，其中v ∈ succ(G, u)，是从u到v移动的成本。
到达成本值：给定顶点v ∈ V，函数g : v 7 → r返回一个非负实数r，这是从给定的初始状态xinit ∈ Xfree到v的路径的成本。我们将使用g∗(v)来表示顶点v在Xfree中可以达到的最优到达成本值。
启发式值：给定顶点v ∈ V，和目标区域Xgoal，函数h : (v, Xgoal) 7 → r返回一个估计值r，这是从v到Xgoal的最优成本；如果v ∈ Xgoal，我们设h(v) = 0。如果它从不高估到达Xgoal的实际成本，那么它就是一个可接受的启发式。在本文中，我们总是假设h是一个可接受的启发式。众所周知，不可接受的启发式可以用来加速搜索，但它们可能导致次优路径。
我们希望解决以下运动规划问题：给定一个有界且连通的开集X ⊂ Rd，集合Xfree和Xobs = X \Xfree，一个初始点xinit ∈ Xfree和一个目标区域Xgoal ⊂ Xfree，找到连接xinit到目标区域Xgoal的最小成本路径。如果不存在这样的路径，那么报告无法找到解决方案。
在下一节中，我们将提出一种迭代算法，该算法找到连接从Xfree随机采样的一系列点的最优路径。该算法基于与RRT_算法中发现的类似的思想，但有一个重要的区别。虽然RRT_算法是基于在添加新顶点后对树进行局部重连，但是提出的算法在每次迭代中都包含了一个重规划步骤，类似于在LPA_和D_算法中实现的，以有效地传播由于包含新顶点而在图的相关部分中发生的变化。因此，提出的算法确保在每次迭代中，都计算出当前图中的最优路径。
相反，RRT*算法并不能保证在任何中间迭代的临时路径是最优的。由于任何算法都将在有限次迭代后终止，因此重要的是要确保，在终止时，返回的路径是最优的，给定到那一点为止的所有可用数据。此外，重要的是要确保在每次迭代中都有效地计算最优路径。这意味着在下一次重新规划步骤中，需要考虑来自前一次迭代的任何先前信息。在我们的实现中，这是通过跟踪图中最“有前途”的顶点（这些是可以成为最优路径的顶点）并在新信息变得可用时更新这些顶点的到达成本值来完成的。已经证明，这相当于在每次迭代后，对变量进行适当的重新排序（以编码更新的信息），类似于在高斯-赛德尔松弛方法中解决固定点问题时所做的事情。

III. RRT#算法 - 概述

给定一个图G = (V, E)，一个初始顶点xinit和一个目标顶点集Xgoal，以下的Bellman类型方程可以用来计算所有顶点的最优到达成本值
g∗(vi) = min vj ∈pred(G,vi) (g∗(vj ) + c(vj , vi)), (1)
其中边界条件是g∗(vi) = 0如果vi = xinit。这个方程可以使用Bellman-Ford算法有效地解决。人们可以通过松弛方程（1）来引入Bellman-Ford算法的Gauss-Seidel版本，以便根据到达成本值。为此，让nk是算法的第k次迭代中的顶点（即，状态）的数量，让gk, ∈ Rnk是nk维向量，其组件是在第k次迭代的算法中，更新了th顺序顶点的到达成本值后的顶点的到达成本值，也就是说，gk, i = gk+1 i 如果vi vo()和gk, i = gk i如果vo() ≺ vi。初始条件设置为g0,0 i = 0对于vi = xinit和g0,0 i = ∞ 对于所有vi ∈ V \ {xinit}。然后，Bellman-Ford算法的Gauss-Seidel迭代可以简洁地写成gk,0 = fG(gk−1,0)，其中
fGo() (gk−1,−1) = min vj ∈pred(G,vo()) (gk−1,−1 j +c(vj , vo())), (2)
和边界条件fGo() (gk−1,−1) = 0如果vo() = xinit。在每次迭代中，gk−1,0的组件被一次更新为gk−1, o() = fGo() (gk−1,−1)其中 gk,0 = gk−1,nk 。 在算法的第k次迭代的th步计算的值fGo()是顶点vo()的一步预测到达成本估计，称为顶点的局部最小到达成本估计，或简称为顶点的lmc值（在中也称为rhs值）。因此，阶段(k, )的顶点vi的lmc值定义为lmck,(vi) = fGi (gk,)对于Gauss-Seidel类型的迭代，如果顶点vi被称为静止的，那么gk,(vi) = lmck,(vi)，这意味着gk, i = fGi (gk,)。否则，它被称为非静止的。 RRT#算法在每次迭代中执行两个任务，即探索和利用。探索任务实现了RRG算法的扩展过程，然后由利用任务跟进，该任务实现了Bellman-Ford算法的Gauss-Seidel版本，如方程（2）所示。下面给出了每个步骤的简要描述。
探索：这一步在Xfree中随机采样一个点，然后通过将其作为当前图中的新顶点，通过连接缺失的边，将基础图向采样点扩展。以下过程是探索步骤的一部分。
采样：Sample : N → Xfree从Xfree返回独立的，同分布的（i.i.d）样本。
最近邻：Nearest返回给定有限集V中，根据给定的距离函数，最接近给定点x的点。
附近的顶点：Near返回给定有限集V中，根据给定的距离函数，最接近给定点x的n个点。
转向：Steer返回以给定状态x为中心的球中的点，该点根据给定的距离函数，最接近另一个给定点xnew。
碰撞检查：给定两点x1, x2 ∈ Xfree，布尔函数ObstacleFree(x1, x2)检查连接这两点的线段是否属于Xfree。如果线段是Xfree的子集，即Line(x1, x2) ⊂ Xfree，它返回True，否则返回False。
图扩展：Extend是一个函数，它将图G向随机采样点xrand扩展最近的顶点。
利用：这一步实现了改进当前顶点的到达成本值的任务，因为新的信息变得可用。它还将对有前途的顶点（见下面的方程（3））和v∗ goal（目标集中具有最低到达成本值的目标顶点）的最低成本路径信息编码为以初始顶点为根的生成树。在每次迭代中，非静止顶点的到达成本值按照它们的f值（即，从初始顶点到通过感兴趣的顶点的目标集的最优路径的成本的低估）的顺序更新，每次迭代中具有较小g值的顶点优先。注意，该算法的工作方式是，只需要一部分顶点（而不是所有顶点）的静止性就足以计算从xinit到Xgoal的最优路径。利用步骤中使用的过程的详细信息如下。
排序：给定一个顶点v ∈ V，函数Key : v 7 → k返回一个实数向量k ∈ R2，其组件是k1(v) = lmc(v) + h(v)和k2(v) = lmc(v)。键的组件分别对应于A*算法中的f-和g值。键之间的优先关系由字典排序确定。给定两个键k1, k2 ∈ R2，布尔函数4 : (k1, k2) 7 → {False, True}当且仅当k11 < k21或（k11 = k21且k12 ≤ k22）时返回True，否则返回False。
有前途的顶点：给定一个图G = (V, E)，其中xinit ∈ V，让g∗(v)是在给定的图G上可以达到的顶点v的最优到达成本值，让v∗ goal = argminv∈V ∩Xgoal g∗(v)。有前途的顶点集Vprom ⊂ V定义为 Vprom = {v : [f(v), g∗(v)] ≺ [f(v∗ goal), g∗(v∗ goal)]}, (3) 其中f(v) = g∗(v)+h(v)。只有有前途的顶点有可能成为从xinit到Xgoal的最优路径的一部分。因此，所有有前途的顶点在每次迭代结束时都必须是静止的。
相关区域：让x∗ goal ∈ Xgoal是目标区域中具有Xgoal中最低最优到达成本值的点，即，x∗ goal = argminx∈Xgoal g∗(x)。Xfree的相关区域是一组点x，其中x的最优到达成本值，加上从x到Xgoal移动的最优成本的估计，小于x∗ goal的最优到达成本值，即， Xrel = {x ∈ Xfree : g∗(x) + h(x) < g∗(x∗ goal)}。 位于Xrel中的点有可能成为从xinit到Xgoal的最优路径的一部分。
重新规划：给定第k次迭代的图Gk = (V k, Ek)，目标区域Xgoal ⊂ Xfree和一个任意向量gk−1,0 ∈ Rnk，它是所有v ∈ V k的到达成本值，其中gk−1,0 i = 0对于v = xinit，函数Replan :(Gk, Xgoal, gk−1,0) 7 → (Gk, Xgoal, gk,0)在所有有前途的顶点都变为静止之前，迭代地对非静止顶点进行操作。Replan函数用于传播图的拓扑变化的影响，因为每次迭代都会添加新的顶点。
顶点的优先级：顶点的优先级与它们关联的键的优先级相同，优先队列用于根据它们各自的键值对图的所有非静止顶点进行排序。以下函数被定义为管理优先队列。
更新队列：函数UpdateQueue根据顶点v的g-和lmc-值改变队列。如果顶点v是非静止的，那么它要么被插入到队列中，要么根据它的最新键值更新它在队列中的优先级，如果它已经在队列中。否则，如果它是一个静止的顶点，那么它将从队列中移除。每一步扩展的顶点的顺序是通过在每一步选择队列中键值最小的顶点来确定的。
查找最小值：函数findmin()返回队列中所有顶点中优先级最高的顶点。这是键值最小的顶点。
删除顶点：函数remove()从队列中删除顶点v。
更新优先级：函数update()通过重新分配顶点v的键值为新的给定键值，改变队列中顶点v的优先级。
插入顶点：给定一个顶点v ∈ V，和一个键值，函数insert()将顶点v和给定的键值一起添加到队列中。

IV. RRT#算法 - 详细信息

RRT#算法的主体在算法1中给出，它与其他RRT变体（RRT，RRG，RRT_等）相似，但有一个显著的例外，它使用所有当前顶点在图中的键值来跟踪顶点的静止性。RRT_和RRT#算法的一个重要区别是，RRT算法计算的树中的所有顶点都有一个基于它们的有限到达成本值的统一类型，而在RRT#算法中，顶点根据它们的一步预测到达成本值的估计有四种不同的类型。在RRT#算法中，每个顶点v都根据其(g(v), lmc(v))对的值被分类为以下四个类别之一：具有有限键值的静态顶点（g(v) < ∞, lmc(v) < ∞且g(v) = lmc(v)），具有无限键值的静态顶点（g(v) = ∞, lmc(v) = ∞），具有有限键值的非静态顶点（g(v) < ∞ , lmc(v) < ∞且g(v) 6 = lmc(v)）和具有无限g-值和有限lmc-值的非静态顶点（g(v) = ∞ , lmc(v) < ∞）。具有无限键值的静态顶点总是非有前途的，而对于其余的情况，顶点可以是有前途的或非有前途的。
算法首先将初始点xinit添加到基础图的顶点集中。然后，它通过从Xfree中随机采样一个点xrand并向xrand扩展图，逐步增长Xfree中的图。然后，Replan过程（在算法3中提供）将新信息传播到整个图中，以改进图中有前途的顶点的到达成本值。所有由采样和扩展步骤产生的计算，后面跟着利用（算法1的第5-7行），形成了算法的单次迭代。这个过程重复给定的固定次数的迭代。最后返回的是以初始顶点为根，包含有前途顶点和v∗ goal的最低成本路径信息的生成树。
这个生成树（算法1中的第7行）包含了每个有前途的顶点和v∗ goal的最低成本路径的信息，这些路径可以在当前图上实现。这是RRT#算法和其他RRT变体（包括RRT算法）之间的关键区别之一。此外，在RRT#算法中，有前途的顶点的g值等于可以通过图的边实现的相应最优到达成本值。这使我们能够在扩展过程中，如果新顶点有任何有前途的邻居顶点，就用一个较小的估计值初始化新顶点的g值。每当图的任何部分出现新的信息时，这个估计都会改进到最好可能的值。因此，图中每个有前途的顶点的g值都会很快收敛到其最优到达成本值。
RRT#算法使用的Extend过程在算法2中给出。在每次迭代中，Extend过程试图将图向随机采样的点xrand ∈ Xfree扩展。首先，在第3行找到图中最近的顶点xnearest，然后在下一行将xnearest向随机采样的点xrand转向。如果连接转向点xnew和xnearest的线段是可行的，那么新点xnew就准备加入到图的顶点集中。然后，在xnew的一些邻域（即，Near过程返回的顶点集）中进行局部搜索，以找到局部最小的到达成本估计值和相应的父顶点。这在算法2的第8-13行中完成。新顶点xnew和所有导致可行路径的扩展都被添加到图的顶点和边集中，这在第14-15行中完成。最后，根据其静止性，决定是否将新顶点插入到优先队列中，这在UpdateQueue过程中完成。新插入的顶点可能是非静止的，如果它有一个有限的lmc值。因此，需要检查生成树，并在必要时执行适当的操作，以更新最低成本路径信息。Replan过程（在算法3中提供）被调用来通过迭代地对图的非静止和有前途的顶点进行操作，更新生成树。它只是从优先队列中弹出最有前途的非静止顶点（如果有的话），并通过将其lmc值赋给其g值，使这个非静止顶点变为静止。然后，它的新g值在其邻居中传播，以便在算法3的第6-10行中改进它们的lmc值。然而，这种信息传播也可能导致一些顶点变得非静止；因此，所有产生的非静止顶点也被插入到优先队列中。这个过程继续，直到优先队列中没有非静止的有前途的顶点为止。
注意，算法3中第2行的终止条件确保了当Replan过程终止时，所有有前途的非静止顶点都被扩展。如果Replan(Gk, Xgoal)过程被允许对图的所有非静止顶点进行操作，那么这显然是正确的，也就是说，如果算法3中第2行的终止条件被替换为“队列不为空”的条件。在这种情况下，Replan过程将扩展所有的顶点，直到它们都变为静止，然后过程才会终止。然而，算法3中第2行的终止条件实际上确保了更多的内容，即，所有有前途的顶点（只有这些顶点）都变为静止，所以没有必要扩展非有前途的顶点。这对于效率很重要，因为一个非有前途的顶点不能成为最优路径的一部分。因此，没有必要扩展非有前途的顶点，从而加快了整个算法的速度。

Algorithm 1: Body of the RRT# Algorithm
RRT#(xinit, Xgoal, X )
    V ← {xinit}; E ← ∅;
    G ← (V , E);
    for k = 1 to N do
        xrand ← Sample(k);
        G ← Extend(G, xrand);
        Replan(G, Xgoal);
        (V , E) ← G; E′ ← ∅;
        foreach x ∈ V do
            E′ ← E′ ∪ {(parent(x), x)}
    return T = (V , E′)

Algorithm 2: Extend Procedure
Extend(G,x)
    (V , E) ← G; E′ ← ∅;
    xnearest ← Nearest(G, x);
    xnew ← Steer(xnearest, x);
    if ObstacleFree(xnearest, xnew) then
        Initialize(xnew, xnearest );
        Xnear ← Near(G, xnew, |V |);
        foreach xnear ∈ Xnear do
            if ObstacleFree(xnear, xnew) then
                if lmc(xnew) > g(xnear) + c(xnear, xnew)
                then
                    lmc(xnew) = g(xnear) + c(xnear, xnew);
                    parent(xnew) = xnear;
                E′ ← E′ ∪ {(xnear, xnew), (xnew, xnear)} ;
        V ← V ∪ {xnew};
        E ← E ∪ E′;
        UpdateQueue(xnew);
    return G′ ← (V , E)

Algorithm 3: Replan Procedure
Replan(G,Xgoal)
    while q.f indmin() ≺ Key(v∗goal) do
        x = q.f indmin();
        g(x) = lmc(x);
        q.delete(x);
        foreach s ∈ succ(G, x) do
        if lmc(s) > g(x) + c(x, s) then
            lmc(s) = g(x) + c(x, s);
            parent(s) = x;
            UpdateQueue(s);

Algorithm 4: Auxiliary Procedures
Initialize(x, x′)
    g(x) ← ∞;
    if x′ = ∅ then
        lmc(x) ← ∞;
        parent(x) ← ∅;
    else
        lmc(x) = g(x′) + c(x′, x);
        parent(x) = x′;
UpdateQueue(x)
    if g(x) 6 = lmc(x) and x ∈ q then
        q.update(x, Key(x));
    else if g(x) 6 = lmc(x) and x /∈ q then
        q.insert(x, Key(x));
    else if g(x) = lmc(x) and x ∈ q then
        q.delete(x);
Key(x)
    return k = (lmc(x) + h(x), lmc(x));

RRT*和RRT#算法计算的树的演变分别在(a)-(d)和(e)-(h)中显示。树的配置(a)，(e)在250次迭代时，(b)，(f)在500次迭代时，©，(g)在2500次迭代时。和(d)，(h)在10000次迭代时。

Informed RRT*

RRT_算法改进解决方案的必要条件是添加一个来自规划问题的子集Xf ⊆ X的状态。对于寻求在R中最小化路径长度的问题 n，这个子集可以通过一个长轴椭球体（一种特殊类型的超椭球体）来估计，Xfb ⊇ Xf，这个长轴椭球体以初始状态和目标状态为焦点。通过拒绝采样一个更大的集合来添加这个子集中的新状态的概率，当问题的维度增加，采样集合的大小增加，或者解决方案接近理论最小值时，这个概率变得任意小。提出了一种简单的方法来直接采样Xfb，这允许创建有信息采样的规划器，如Informed RRT_。
Informed RRT_使用启发式来缩小规划问题到原始域的子集。这使得它本质上依赖于当前的解决方案成本，因为当与规划问题本身相关的长轴椭球体更大时，它不能集中搜索。同样，它只能将子集缩小到由最优解决方案定义的下界。_
Informed RRT_能够在比RRT_少得多的迭代次数内找到接近最优的解决方案。有信息子集的直接采样比全局采样更快地增加了围绕最优解的密度，从而增加了改进解决方案和进一步集中搜索的概率。相比之下，RRT在整个规划域上具有均匀的密度，改进解决方案实际上降低了找到进一步改进的概率。
Informed RRT是对RRT_的一个简单修改，展示了明显的改进。在模拟中，它在简单配置上的表现与现有的RRT_算法一样好，并且在配置变得更困难时显示出数量级的改进。由于其专注的搜索，该算法对规划问题的维度和域的依赖性较小，以及更早找到更好的拓扑不同路径的能力。它还能够在等价计算的情况下找到比RRT_更紧密的最优解，并且在没有障碍的情况下可以在有限时间内找到最优解。它也可以与其他算法，如路径平滑，结合使用，以进一步减少搜索空间。
Informed RRT算法明确计算Xfb，并直接从中采样。与路径偏置不同，它对最优解的同伦类没有做任何假设，与启发式偏置不同，它不探索不能改进解决方案的状态。由于它基于RRT，所以它能够在搜索的整个过程中保留在Xfb中找到的所有状态，与Anytime RRTs不同。通过直接采样Xfb，它总是采样潜在的改进，无论Xfb相对于X的大小如何。这使得它能够有效地工作，无论规划问题的大小或当前解决方案的相对成本接近理论最小值，与样本拒绝和图剪枝方法不同。在问题中，启发式没有提供任何额外的信息，它的表现与RRT完全相同。
直接采样方法允许创建有信息的采样规划器。这样的规划器，被称为Informed RRT，被提出来展示有信息的增量搜索的优点。Informed RRT_的行为与RRT_相同，直到找到第一个解决方案，之后它只从由可接受的启发式定义的状态子集中采样，以可能改进解决方案。这个子集隐含地平衡了利用与探索，并且不需要额外的调整（即，没有额外的参数）或假设（即，搜索所有相关的同伦类）。虽然启发式可能并不总是改进搜索，但它们在实际规划中的突出表现证明了它们的实用性。在它们没有提供额外信息的情况下（例如，当被告知的子集包括整个规划问题时），Informed RRT_等同于RRT。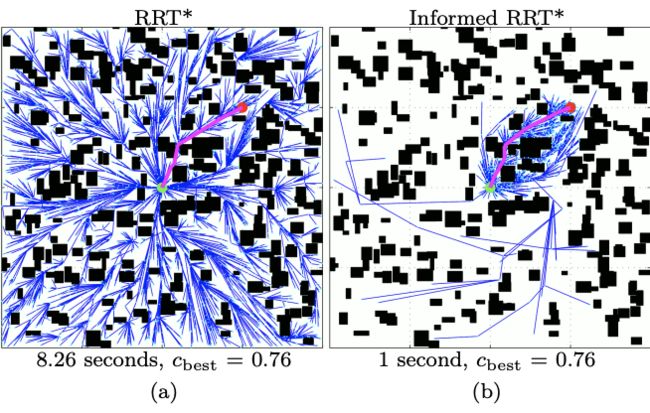

RRT_和Informed RRT_在随机世界上找到的等价成本解决方案。在找到初始解决方案后，Informed RRT_将搜索集中在状态空间的椭球形有信息子集Xfb ⊆ X上，该子集包含了所有可以改进当前解决方案的状态，无论同伦类如何。这使得Informed RRT_能够比RRT*更快地找到更好的解决方案，而不需要任何额外的用户调整参数。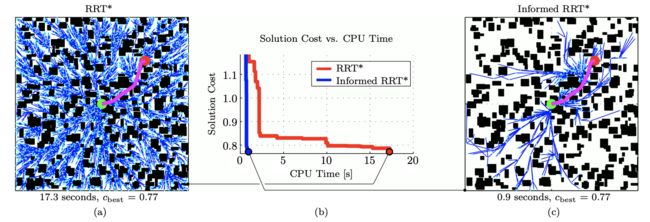

随机世界问题上RRT_和Informed RRT_的解决方案成本与计算时间。两个规划器都运行到找到相同成本的解决方案。图（a, c）显示了最终结果，而图（b）显示了解决方案成本与计算时间。从图（a）可以看出，RRT_在探索规划问题的区域时花费了大量的计算资源，这些区域无法改进当前的解决方案，而图（c）展示了Informed RRT_是如何集中搜索的。

在没有障碍物的情况下，Informed RRT*收敛到机器零的最优。起始和目标状态分别以绿色和红色显示，它们之间的距离为100个单位。当前的解决方案以洋红色突出显示，用于说明的椭球形采样域，Xfb，以灰色虚线显示。改进解决方案会减小采样域的大小，创建一个反馈效应，使其收敛到理论最小值的机器零。图（a）显示了59次迭代后的第一个解决方案，（b）在175次迭代后，和（c），在1142次迭代后的最终解决方案，此时椭圆已经退化为一条从开始到目标的线。

算法伪代码

II. 减少RRT树增长的一些方法

A. 以前的工作
以前的工作是通过样本偏置、基于启发式的样本拒绝、基于启发式的图剪枝和/或迭代搜索来专注RRT和RRT*。
1）样本偏置：样本偏置试图通过偏置从X中抽取的样本的分布，增加从Xf中抽取状态的频率。这继续添加来自Xf之外的状态，这些状态不能改进解决方案。它还导致在被搜索的问题上的非均匀密度，违反了一个关键的RRT假设。
a) 启发式偏置采样：启发式偏置采样试图通过用启发式估计对每个状态进行加权，增加采样Xf的概率。它被用来改进常规的RRT，由Urmson和Simmons [5]在启发式引导的RRT (hRRT)中，通过选择状态的概率与它们的启发式成本成反比。hRRT被证明找到比RRT更好的解决方案；然而，使用RRTs意味着解决方案几乎肯定是次优的[7]。Kiesel等人[11]使用两阶段过程来创建他们的f-biasing技术中的RRT_启发式。首先解决规划问题的粗略抽象，以提供每个离散状态的启发式成本。然后，RRT_通过随机选择一个离散状态，并在其中使用连续均匀分布进行采样，来采样新状态。离散采样被偏置，使得属于抽象解决方案的状态具有最高的选择概率。这种技术为RRT算法的整个持续时间提供了启发式偏置；然而，为了考虑离散抽象，它保持选择每个状态的非零概率。因此，仍然会采样到不能改进当前解决方案的状态。
b) 路径偏置：路径偏置采样试图通过在当前解决方案路径周围采样，增加采样Xf的频率。这假设当前解决方案要么与最优解同伦，要么只被小障碍物分隔。由于这个假设通常不成立，路径偏置算法必须继续全局采样以避免局部最优。这两种采样方法的比例通常是用户调整的参数。
Alterovitz等人[12]使用路径偏置开发了快速探索路线图(RRM)。一旦找到初始解决方案，RRM的每次迭代要么采样一个新状态，要么从当前解决方案中选择一个现有状态并对其进行精化。路径精化通过将选定的状态连接到其邻居，从而产生一个图而不是一棵树。Akgun和Stilman[13]在他们的双树版本的RRT中使用路径偏置。一旦找到初始解决方案，该算法将用户指定的百分比的迭代用于精化当前解决方案。它通过随机选择解决方案路径中的一个状态，然后显式地从其Voronoi区域中采样来实现这一点。这增加了改进当前路径的概率，但以牺牲探索其他同伦类为代价。他们的算法也在探索状态空间时使用样本拒绝（第II-B.2节）。
Nasir等人[14]在他们的RRT-Smart算法中结合了路径偏置和平滑。当找到解决方案时，RRT*-Smart首先将路径平滑并减少到最小的状态数量，然后使用这些状态作为进一步采样的偏置。这将路径平滑算法的复杂性添加到规划器中，同时仍然需要全局采样以避免局部最优。虽然路径平滑快速降低了当前解决方案的成本，但它也可能通过减少绘制样本的偏置点的数量，进一步违反了RRT关于均匀密度的假设。
Kim等人[15]在他们的Cloud RRT算法中使用可见性分析生成初始偏置。当找到解决方案时，这个偏置被更新，以进一步集中路径附近的采样。
2）基于启发式的样本拒绝：基于启发式的样本拒绝试图通过在X上使用拒绝采样来采样Xfb，从而增加实时采样Xf的速率。从较大的分布中抽取的样本要么被保留，要么根据它们的启发式值被拒绝。Akgun和Stilman[13]在他们的算法中使用了这样的技术。虽然这对于单次迭代来说计算成本很低，但是找到Xfb中的单个状态所需的迭代次数与其相对于采样域的大小成正比。当解决方案接近理论最小值或规划域增长时，这变得不平凡。
Otte和Correll[8]在他们的并行化C-FOREST算法中从规划域的子集中抽取样本。这个子集被定义为包围椭球形有信息子集的超矩形。虽然这改善了样本拒绝的性能，但随着问题维度的增加，其效用会减少（注2）。
3）图剪枝：图剪枝试图通过使用启发式函数将图限制在Xfb，从而增加实时探索Xf。规划图中的启发式成本大于当前解决方案的状态被周期性地移除，同时继续全局采样。RRTs的空间填充性质使剪枝图的扩展偏向于Xfb的边界。在子集被填充后，只有来自Xfb本身的样本才能向图中添加新状态。因此，图剪枝在贪婪地填充目标子集后，就变成了一种拒绝采样方法。由于向RRT添加新状态需要调用最近邻算法，图剪枝将比简单的样本拒绝更加计算昂贵，同时仍然受到相同的概率限制。
4）随时RRTs：Ferguson和Stentz[6]认识到，解决方案从上面限制了可以进一步改进的状态子集。他们的迭代RRT方法，Anytime RRTs，解决了一系列独立的规划问题，这些问题的域由前一个解决方案定义。他们将这些域表示为椭圆，但没有讨论如何生成样本。限制规划域鼓励每个RRT找到比前一个更好的解决方案；然而，为了做到这一点，他们必须丢弃已经在Xfb中找到的状态。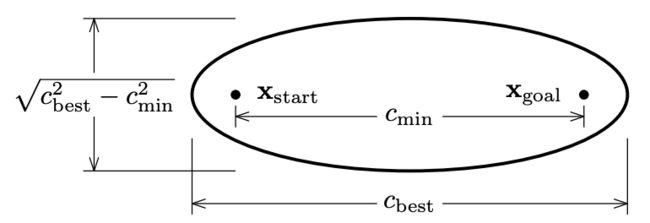

对于在R中寻求最小化路径长度的问题 n，有信息的采样域，Xfb，是一个以初始状态，xstart，和目标状态，xgoal，为焦点的椭圆。椭圆的形状取决于初始状态和目标状态，两者之间的理论最小成本，cmin，以及迄今为止找到的最佳解决方案的成本，cbest。椭圆的偏心率由cmin/cbest给出。

III. Informed RRT*中椭球形有信息子集的分析

给定一个正的成本函数，从xstart到xgoal的最优路径的成本，约束通过x ∈ X，f (x)，等于从xstart到x的最优路径的成本，g (x)，加上从x到xgoal的最优路径的成本，h (x)。由于基于RRT的算法渐进地从上面接近每个状态的最优路径，一个可接受的启发式估计，fb(·)，必须估计这两个术语。可接受性的充分条件是，组件，gb(·)和bh (·)，分别是g (·)和h (·)的可接受启发式。
对于寻求在R中最小化路径长度的问题 n，欧几里得距离是两个术语的可接受启发式（即使有运动约束）。那么，可能改进当前解决方案的状态的有信息子集，Xfb ⊇ Xf，可以用当前解决方案的成本，cbest，的封闭形式来表示， Xfb = x ∈ X ||xstart − x||2 + ||x − xgoal||2 ≤ cbest , 这是n维长轴椭球（即，特殊的超椭球）的一般方程。焦点是xstart和xgoal，横向直径是cbest，共轭直径是p c 2 best - c 2 min (图4)。
fb(·)的可接受性使得添加一个状态在Xfb是改进解决方案的必要条件。由于RRT的空间填充性质，添加这样一个状态的概率很快就变成了采样这样一个状态的概率1。 因此，通过均匀采样一个更大的子集，x i+1 ∼ U (Xs)，Xs ⊇ Xfb，在任何迭代中改进解决方案的概率小于或等于集合度量λ (·)的比率， P注2（矩形拒绝采样）：设Xs是一个紧密包围有信息子集的超矩形（即，每个边的宽度对应于长轴椭球体的直径）[8]。从（3）中，从Xs均匀抽取的样本在Xfb中的概率为ζn 2n，随着n的增加，这个概率迅速减小。例如，当n = 6时，这给出了每次迭代通过拒绝采样改进解决方案的最大8%的概率，无论具体的解决方案、问题或算法参数如何。
定理1（无障碍线性收敛）：对有信息子集的均匀采样，x ∼ U Xfb ，最佳解决方案的成本，cbest，在没有障碍的情况下，线性收敛到理论最小值，cmin。
证明：状态的启发式值等于通过状态并且焦点在xstart和xgoal的长轴椭球体的横向直径。对于均匀采样，期望值是[20] E h fb(x) inc2 best+c 2 min (n+1)cbest . (4) 我们假设RRT_的重连参数大于有信息子集的直径，就像RRT_的渐进最优性的证明假设η大于规划问题的直径一样[7]。解决方案成本的期望值，c i best，然后是从直径为c i−1 best的长轴椭球体中抽取的样本的启发式成本的期望值，即，E c i best = E h fb V. INFORMED RRT 我们在Algs. 1和2中提出了一个使用直接有信息采样的示例算法，Informed RRT*。它与[7]中提出的RRT_完全相同，只是增加了第3行、第6行、第7行、第30行和第31行。像RRT_一样，它通过在状态空间中逐步构建树T = (V, E)，由一组顶点V ⊆ Xfree和边E ⊆ Xfree × Xfree组成，来搜索规划问题的最优路径σ ∗ 。新的顶点是通过在自由空间中向随机选择的状态增长图来添加的。每个新顶点都会对图进行重连，使得附近顶点的成本最小化。
该算法与RRT_的不同之处在于，一旦找到解决方案，它就会将搜索集中在可以改进解决方案的规划问题的部分。它通过直接采样椭球形启发式来实现这一点。当找到解决方案时（第30行），Informed RRT_将它们添加到可能的解决方案列表中（第31行）。它使用这个列表的最小值（第6行）来计算和直接采样Xfb（第7行）。按照惯例，我们认为一个空集的最小值是无穷大。新的子函数在下面描述，而与RRT*共有的子函数的描述可以在[7]中找到：
Sample：给定两个姿态，xfrom, xto ∈ Xfree和一个最大启发式值，cmax ∈ R，函数Sample (xfrom, xto, cmax)返回从状态空间中独立且同分布（i.i.d.）抽取的样本，xnew ∈ X，使得从xstart到xgoal的最优路径的成本，约束通过xnew，小于cmax，如第III节和Alg. 2所述。在大多数规划问题中，xfrom ≡ xstart, xto ≡ xgoal，Alg. 2的第2行到第4行可以在问题开始时计算一次。
InGoalRegion：给定一个姿态，x ∈ Xfree，函数InGoalRegion (x)如果状态在规划问题定义的目标区域，Xgoal，中，返回True，否则返回False。一个常见的目标区域是一个以目标为中心的半径为rgoal的球，即， Xgoal = x ∈ Xfree ||x − xgoal||2 ≤ rgoal 。
RotationToWorldFrame：给定两个姿态作为超椭球体的焦点，xfrom, xto ∈ X，函数RotationToWorldFrame (xfrom, xto)返回从超椭球体对齐的框架到世界框架的旋转矩阵，C ∈ SO (n)，如（6）所示。如前所述，在大多数规划问题中，这个旋转矩阵只需要在问题开始时计算一次。
SampleUnitNBall：函数SampleUnitNBall返回从单位半径的n球体的体积中均匀抽取的样本，即xball ∼ U (Xball)。这个n球体以原点为中心。
A. 计算重连半径 在每次迭代中，重连半径rRRT∗必须足够大，以保证几乎肯定的渐进收敛，同时又要足够小，以只生成可处理的数量的重连候选者。Karaman和Frazzoli[7]提出了这个重连半径的下界，这个下界是以问题空间的度量和图中顶点的数量为基础的。他们的表达式假设样本的分布是单位平方的均匀分布。由于Informed RRT_均匀地采样可以改进解决方案的规划问题的子集，所以可以从这个有信息子集的度量和其中的相关顶点来计算重连半径。这个更新的半径减少了必要的重连数量，进一步改善了Informed RRT_的性能。正在进行的工作集中在找到这个表达式的确切形式，但是[7]提供的半径似乎是合适的。这个表达式也存在一个k-最近邻版本。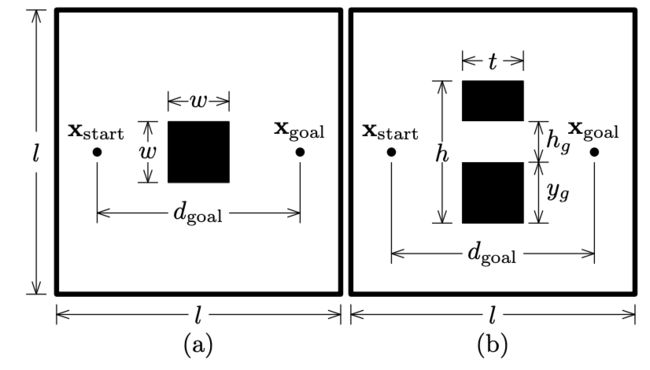

在第VI节中使用的两个规划问题。障碍物的宽度，w，和间隙的位置，yg，对于每次实验运行都是随机选择的。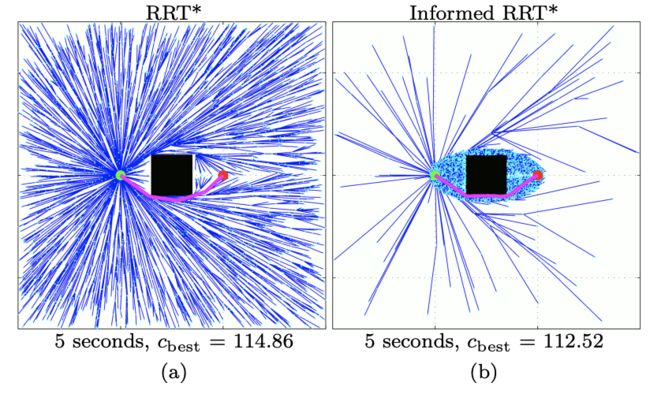

在5秒内对(a)的一个例子，对于一个最优解决方案成本为112.01的问题。注意到，障碍物的存在为椭球形子集提供了一个下界，但是Informed RRT_仍然比RRT_搜索了一个显著减小的域，从而增加了收敛速率和最终解决方案的质量。

对于一个3%偏离中心的间隙的图5(b)的一个例子。通过将搜索空间集中在包含最优解的规划问题的区域的子集上，Informed RRT_能够在4.00秒内找到通过狭窄开口的路径，而RRT_需要12.32秒。

综合全局和增量信息的GuILD

简单来说,GuILD利用搜索树信息分解原始问题,定义局部采样子集,从而使采样更有针对性和高效,加速了基于采样的最优运动规划的收敛。Guided Incremental Local Densification (GuILD)，它利用搜索树中顶点的到达成本的改进来指导采样策略，从而更快地发现更短的路径。GuILD可以与任何基于采样的运动规划器结合使用，例如RRT_，Informed RRT_等。
这是一种基于采样的运动规划器，利用搜索树中的顶点到达成本的改善来指导采样策略，从而更快地发现更短的路径。该算法的原理是，当发现到搜索树中的某个顶点的更短路径时，就可以缩小从该顶点到目标的Informed Set，从而减少无效的采样。

1. 提出了GuILD框架,可以有效利用搜索树信息来聚焦样本,从而指导增量密化。
2. 将原始的问题分解成两个子问题,引入了"灯塔"的概念,灯塔是一个搜索树中的顶点。
3. 定义了由灯塔诱导的局部子集,并比较了它们与已知集的理论属性。
4. 提出了几种BEACONSELECTOR策略,包括一种敌对多臂老虎机算法。
5. 在各种规划域中进行了实验比较,结果表明无论BEACONSELECTOR的选择如何,GuILD都优于已知集密化基线。
6. GuILD在高维规划问题以及包含难以采样同伦类的规划域中表现出色。

算法核心原理：GuILD的核心思想是利用搜索树中顶点的到达成本的改进来缩小采样空间，从而更有可能采样到更优的点。具体来说，GuILD维护了一个Informed Set (IS)，它是一个包含所有可能产生更短路径的点的集合。IS的大小取决于当前最优路径的长度和欧几里得启发式。GuILD还维护了一个Local Subset (LS)，它是一个包含所有到达成本有所改进的点的集合。LS的大小取决于到达成本的改进量和一个阈值参数。GuILD的采样策略是从IS和LS中按一定的概率进行采样，其中LS的采样概率随着到达成本的改进量的增加而增加。这样，GuILD可以在全局和局部之间进行平衡，从而更快地发现更短的路径。
关键步骤：GuILD的关键步骤如下：

• 初始化：从配置空间中随机采样一个点作为搜索树的根节点，将其加入到IS和LS中。
• 迭代：重复以下步骤，直到找到一条从起点到目标的路径或者达到最大迭代次数。
  • 采样：从IS和LS中按一定的概率进行采样，得到一个新的点。
  • 扩展：在搜索树中找到与新点最近的节点，如果两者之间的路径是可行的，就将新点作为搜索树的一个新节点，并连接到最近的节点。
  • 更新：更新新节点的到达成本，如果新节点到目标的距离小于当前最优路径的长度，就更新最优路径。如果新节点的到达成本有所改进，就将其加入到LS中。如果新节点到目标的距离小于IS的边界，就将其加入到IS中。

GuILD算法：

• 初始化搜索树T，将起点xs加入T，设置初始路径ξ为xs到xt的直线，设置初始Informed Set IS为整个配置空间X。
• 重复以下步骤，直到找到一条满足条件的路径或达到最大迭代次数：
  • 从IS中采样一个点x，如果x与T中的任何顶点相连，则将x加入T，并更新T中的边和顶点成本。
  • 如果x与xt相连，则更新路径ξ为T中的最短路径，并更新IS为{x|x ∈ X , h(xs, x) + h(x, xt) ≤ c(ξ)}。
  • 对于T中的每个顶点xv，计算其到目标的Informed Set ISv，并从ISv中采样一个点xv’，如果xv’与xv相连，则将xv’加入T，并更新T中的边和顶点成本。
  • 如果xv’与xt相连，则更新路径ξ为T中的最短路径，并更新IS为{x|x ∈ X , h(xs, x) + h(x, xt) ≤ c(ξ)}。

输入：配置空间X，起点xs，目标xt，最大迭代次数N
输出：一条从xs到xt的路径ξ或者空

初始化搜索树T，将xs加入T
设置初始路径ξ为xs到xt的直线
设置初始Informed Set IS为整个配置空间X
设置迭代次数i为0

当i < N时，重复以下步骤：
    从IS中采样一个点x
    如果x与T中的任何顶点相连，则：
        将x加入T，并更新T中的边和顶点成本
        如果x与xt相连，则：
            更新路径ξ为T中的最短路径
            更新IS为{x|x ∈ X , h(xs, x) + h(x, xt) ≤ c(ξ)}
    对于T中的每个顶点xv，计算其到目标的Informed Set ISv，并从ISv中采样一个点xv'
    如果xv'与xv相连，则：
        将xv'加入T，并更新T中的边和顶点成本
        如果xv'与xt相连，则：
            更新路径ξ为T中的最短路径
            更新IS为{x|x ∈ X , h(xs, x) + h(x, xt) ≤ c(ξ)}
    i = i + 1

如果路径ξ存在，则返回路径ξ
否则，返回空
#其中，h(x, y)表示x和y之间的欧几里得距离，c(ξ)表示路径ξ的长度。

GuILD框架主要优势：

1. 更高的性能：无论信标选择器如何，GuILD在一系列规划领域中都优于现有的最先进的Informed Set密集化基线。特别是在简单的规划领域，GuILD能够带来适度的改进，并在处理困难领域时表现出色[1]。
2. 更高的采样效率：在实验中，无论信标选择器如何，GuILD的采样效率都比从Informed Set采样更高。这支持了GuILD的假设，即所有三个GuILD选择器都能达到相当的采样效率，这表明他们的关键在于如何选择信标，而不是信标的具体选择[3]。
3. 自动聚焦采样：在低成本同源性规划问题中，GuILD能够自动聚焦采样，以通过这些狭窄的通道提供路径。在Trap环境中，GuILD实例能够在大约1100-1200个样本中识别出狭窄的通道，并快速提供路径[2]。
4. 灵活性：GuILD框架可以轻松（并且高效地）融入任何基于采样的最优运动规划算法[5]。
5. 利用搜索树的信息：GuILD框架的一个核心观点是，即使规划器未能发现更短的路径，搜索树中仍然包含有价值的信息，可以用来指导后续的路径搜索和优化[3]。

总的来说，GuILD框架的优势主要体现在其高效的性能、采样效率、自动聚焦采样的能力，以及其灵活性和对搜索树信息的有效利用。

(a) Informed Set和(b) GuILD引导的Local Subsets的比较。为了进一步缩小Informed Set的范围，GuILD选择了一个信标（绿色），并利用搜索树中的信息将原始问题分解为两个较小的问题。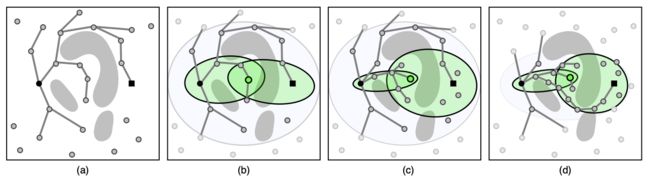

(a) 初始解。 (b) GuILD选择一个信标并引导Local Subsets（绿色），它们没有覆盖狭窄的通道。 © 规划器没有找到一条更短的路径到达目标，所以Informed Set保持不变。但是，GuILD利用搜索树中到达成本的改善来更新Local Subsets。起点-信标集缩小以进一步聚焦采样，而信标-目标集之间的剩余余量用于扩展信标-目标集。Local Subsets现在覆盖了狭窄的通道，聚焦采样在Informed Set内以快速收敛到(d)最优解。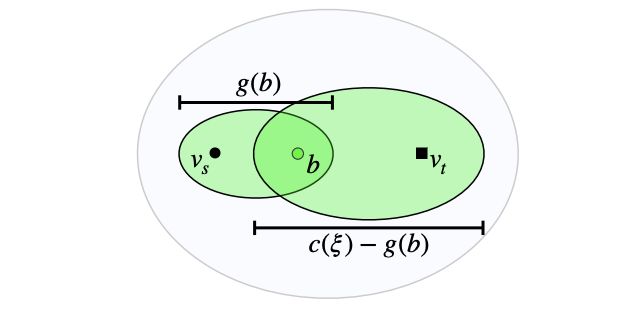

Local Subsets ELS（绿色）由信标b定义， 以及搜索树上的到达成本g(b)和当前最优解的成本c(ξ)。

小结：

本文介绍了“基于采样的路径规划常用算法”，介绍的算法有很多种，但其实都是围绕PRM图搜索、RRT树搜索做的优化、组合的变种。
Sample base plan：这是一种基于样本的规划方法，它通过生成大量的样本点来寻找最优解。这种方法的优点是可以处理高维度和复杂的问题，因为它不需要对整个问题空间进行详细的搜索。然而，这种方法的缺点是可能会产生次优的解决方案，因为它并不总是能找到全局最优解⁴。此外，如果样本点的生成和选择方法不合适，可能会导致效率低下⁵。
尽管这些算法在实现细节上有所不同，但它们都遵循了基于采样的路径规划算法的基本框架，即采样、构建图或树、碰撞检测和路径搜索。这些共同的处理流程使得这些算法能够在各种复杂的环境中进行有效的路径规划。具体选择哪种算法，需要根据实际应用的需求和环境条件来决定。
基于采样的路径规划算法的共同处理流程主要包括以下几个步骤
** a.采样**：在配置空间中随机撒点，生成一组采样点。
** b.构建图或树**：根据采样点之间的关系（例如距离、连通性等），构建一个图或树来表示整个配置空间。
** c.碰撞检测**：检查采样点和采样点之间的连线是否与障碍物发生碰撞，如果有碰撞，则舍弃这些采样点或连线。
** d.路径搜索**：在构建的图或树上搜索一条从起点到终点的路径。
这个流程是基于采样的路径规划算法的基本框架，不同的算法可能会在这个基础上添加一些额外的步骤，例如概率路图算法（PRM）的学习阶段和查询阶段，快速随机扩展树算法（RRT）的树扩展过程，RRT*算法的路径优化过程等。这些算法的具体实现和优化方法可能会有所不同，但它们的核心思想都是通过采样和搜索来寻找一条满足特定条件的路径。
基于采样的路径规划算法，如概率路线图（PRM）、快速搜索随机树（RRT）、RRT_、RRT#、Informed-RRT_和GuILD，虽然在实现细节上有所不同，但它们都遵循了一些共同的处理流程，包括采样、构建图或树、碰撞检测和路径搜索。这些共同的处理流程构成了这类算法的基本框架。
然而，这些算法在具体实现这些处理流程时，会有一些重要的差异。主要差异:

1. PRM属于多查询算法,可用于离线全局规划;RRT属于单查询算法,适用于在线规划。
2. PRM采用批量全局采样;RRT采用增量式采样。PRM覆盖整个空间,RRT增量扩展。
3. PRM构建无向图(可能有环),RRT构建有向树。
4. PRM全局在图上搜索路径,RRT从根节点增量搜索。
5. RRT*、Informed-RRT*、GuILD在RRT基础上引入了贪心策略、启发式、预构建路线图等机制进行加速和优化。

更详细的介绍他们之间差异:

1. 采样范围:全局vs增量
   • PRM:预处理阶段进行全局批量采样
   • RRT/RRT_/_:增量迭代采样
   • GuILD:在增量迭代采样的基础上结合全局Roadmap
2. 数据表示:图vs树
   • PRM:构建路线图(图结构)
   • RRT/RRT#:构建树结构
   • RRG/GuILD:既有树结构,也结合路线图
3. 搜索策略:全局vs增量
   • PRM:全局搜索路径
   • RRT/RRT*/RRT#:增量构建搜索树
   • GuILD:在RRT的搜索树上结合全局路线图搜索
4. 是否利用额外信息进行加速和优化
   • RRT*/RRT#:在RRT上增加贪心策略
   • Informed-RRT*:集成启发式采样
   • GuILD:集成局部子集采样
5. 时间性能

• PRM:两阶段分离,预处理时间长
• RRT系列算法:适合在线规划