C++之unordered_map/set的使用

前面我们已经学习了STL中底层为红黑树结构的一系列关联式容器——set/multiset 和 map/multimap(C++98).

---

unordered系列关联式容器

在C++98中, STL提供了底层为红黑树结构的一系列关联式容器, 在查询时效率可达到log2N,即最差情况下需要比较红黑树的高度次, 当树中的节点非常多时, 查询效率也不理想.

最好的查询是, 进行很少的比较次数就能够将元素找到, 因此在C++11中, STL又提供了4个unordered系列的关联式容器, 这四个容器与红黑树结构的关联式容器使用方式基本类似, 只是其底层结构不同.

---

map,set系列容器和unordered_map,unordered_set系列容器的区别 

1.它们的底层结构是不一样的：

set/multiset 和 map/multimap它们的底层结构是红黑树, 而unordered系列的——unordered_map/unordered_multimap, unordered_set/unordered_multiset它们的底层是哈希表.

unordered系列中, 带multi的和不带multi的区别也是允许键值重复出现和不允许重复出现的问题.

2.从名字上我们其实就能得出它们的第二个区别:

unordered是无序的意思, 所以map和set我们用迭代器遍历, 得到的是有序的序列, unordered系列去遍历的话, 得到的是无序的, 单从使用上来说最大的区别就是有没有序的问题.

3.map和set系列它们的迭代器是双向迭代器, 而unordered系列它们的迭代器是单向迭代器.

4. unorder _ map 容器通过键访问单个元素的速度比 map 容器快, 尽管它们通过元素的子集进行范围迭代的效率通常较低.(和底层实现有关)

---

 unordered_map和unordered_set的使用

单从使用来说, 这和set/multiset 和 map/multimap的使用用法基本一致, 常用的接口都差不多.

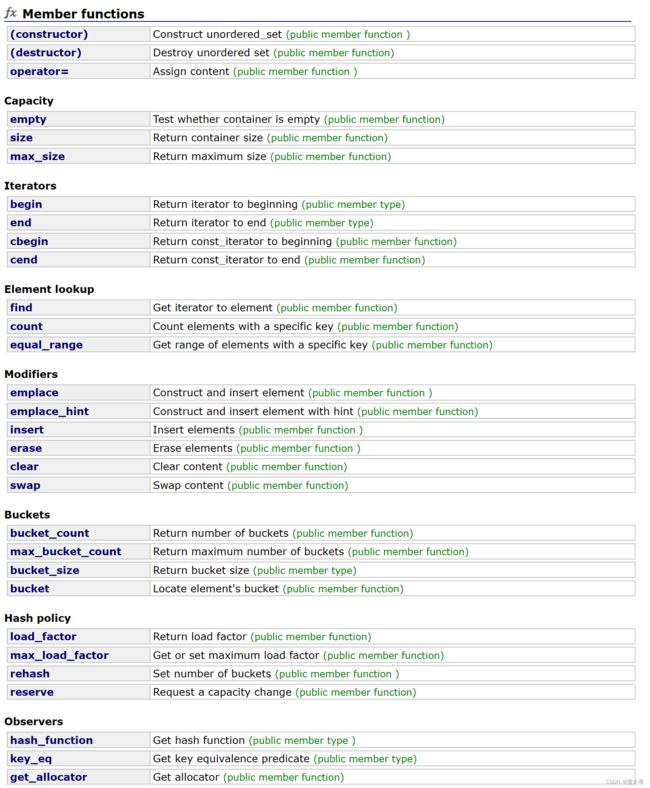
unordered_map的接口:

unordered_map的构造:

函数声明	功能介绍
unordered_map	构造不同格式的unordered_map对象

 unordered_map的容量:

函数声明	功能介绍
bool empty() const	检测unordered_map是否为空
size_t size() const	获取unordered_map的有效元素个数

unordered_map的迭代器:

函数声明	功能介绍
begin	返回unordered_map第一个元素的迭代器
end	返回unordered_map最后一个元素下一个位置的迭代器
cbegin	返回unordered_map第一个元素的const迭代器
cend	返回unordered_map最后一个元素下一个位置的const迭代器

unordered_map的元素访问:

函数声明	功能介绍
operator[]	返回与key对应的value

注意: 该函数中实际调用哈希桶的插入操作, 用参数key与V()构造一个默认值往底层哈希桶
中插入, 如果key不在哈希桶中, 插入成功, 返回V(); 插入失败, 说明key已经在哈希桶中,
将key对应的value返回

unordered_map的查询:

函数声明	功能介绍
iterator find(const K& key)	返回key在哈希桶中的位置
size_t count(const K& key)	返回哈希桶中关键码为key的键值对的个数

注意: unordered_map中key是不能重复的，因此count函数的返回值最大为1 

unordered_map的修改:

函数声明	功能介绍
insert	向容器中插入键值对
erase	删除容器中的键值对
void clear()	清空容器中有效元素个数
void swap(unordered_map&)	交换两个容器中的元素

unordered_map的桶操作:

函数声明	功能介绍
size_t bucket_count()const	返回哈希桶中桶的总个数
size_t bucket_size(size_t n)const	返回n号桶中有效元素的总个数
size_t bucket(const K& key)	返回元素key所在的桶号

它的迭代器没有rbegin、rend, 因为它的迭代器是单向的，不支持反向遍历。

---

 unordered_set的接口:

 接口也都差不多,只是set系列的没有[]和at接口.

#include
#include
#include
using namespace std;

int main()
{
	set s1;
	unordered_set s2;

	s1.insert(1);
	s1.insert(5);
	s1.insert(4);
	s1.insert(3);
	s1.insert(8);
	for (set::iterator it = s1.begin(); it != s1.end(); it++)
		cout << *it << " ";
//
	cout << endl;
//
	s2.insert(1);
	s2.insert(5);
	s2.insert(4);
	s2.insert(3);
	s2.insert(8);
	for (unordered_set::iterator it = s2.begin(); it != s2.end(); it++)
		cout << *it << " ";

	return 0;
}

 

可以看到set按迭代器访问是有序的, unordered_set按迭代器访问是按照插入顺序访问的, unordered_map也是一样.

---

set与unordered_set性能对比 

void test2()
{
	srand(time(nullptr));
	size_t N = 1000000;
	unordered_set us;
	set s;

	vector v;
	v.reserve(N);
	for (size_t i = 0; i < N; i++)
	{
		v.push_back(rand()+i);//减少重复值
	}

	size_t begin1 = clock();
	for (auto& e : v)
		s.insert(e);
	size_t end1= clock();
	cout << "set insert:" << end1 - begin1 << endl;

	size_t begin2 = clock();
	for (auto& e : v)
		us.insert(e);
	size_t end2 = clock();
	cout << "unordered_set insert:" << end2 - begin2 << endl;

	size_t begin3 = clock();
	for (auto& e : v)
		s.find(e);
	size_t end3 = clock();
	cout << "set find:" << end3- begin3 << endl;

	size_t begin4 = clock();
	for (auto& e : v)
		us.find(e);
	size_t end4 = clock();
	cout << "unordered_set find:" << end4 - begin4 << endl;

	size_t begin5 = clock();
	for (auto& e : v)
		s.erase(e);
	size_t end5 = clock();
	cout << "set erase:" << end5 - begin5 << endl;

	size_t begin6 = clock();
	for (auto& e : v)
		us.erase(e);
	size_t end6 = clock();
	cout << "unordered_set erase:" << end6 - begin6 << endl;

}

所以, 综合而言, unordered系列的效率是比较高的, 尤其是find的效率.

---

OJ例题

349. 两个数组的交集 - 力扣（LeetCode） 

map和set的例题-CSDN博客

之前有用set的解法, 排序加去重可以解决, 现在可以用unordered_set, unordered_set虽然不能排序, 但是也是可以去重的, 首先我们先对两个数组进行去重, 然后, 我们遍历其中一个数组, 遍历的同时去依次判断当前元素在不在另一个数组中, 如果在就是交集。

---

 350. 两个数组的交集 II - 力扣（LeetCode）

返回结果中每个元素出现的次数, 应与元素在两个数组中都出现的次数一致(如果在两数组中出现次数不一致,则考虑取较小值), 但是它没有要去输出结果中每个元素是唯一的。 

---

 

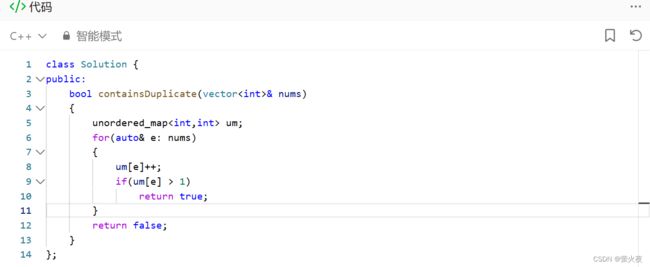
统计次数, 判断有没有次数大于1的就行了:

---

 884. 两句话中的不常见单词 - 力扣（LeetCode）

这道题其实可以求转化成两个字符串合并后, 只出现一次的单词.