【算法系列】时间复杂度、深搜(连通性、剪枝)、宽搜、Flood Fill、图论
目录
- 时间复杂度介绍
- 前言
- 一、深搜
-
- 1.1 深搜思想
- 1.2 基础题目
-
- 1.2.1 排列数字
- 1.2.2 n-皇后问题
- 1.3 DFS中的连通性(能走到，不能保证最短)DFS、BFS均可以求解
-
- 1.3.1 迷宫
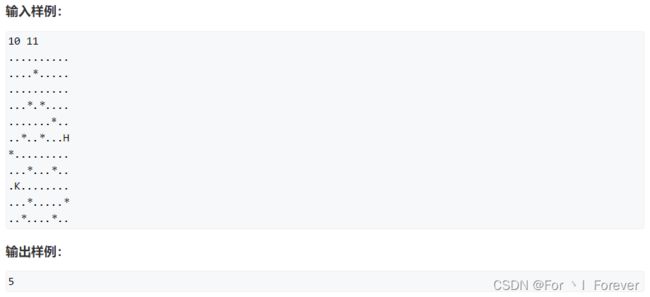
- 1.3.2 红与黑
- 1.4 DFS中的搜索顺序
-
- 1.4.1 马走日
- 1.4.2 单词接龙
- 1.4.3 分成互质组(待补充)
- 1.5 DFS剪枝
-
- 1.5.1 小猫爬山
- 1.5.2 数独
- 二、宽搜
-
- 2.0 宽搜模板
- 2.1 宽搜类型
- 2.2 基础题目
-
- 2.2.1 献给阿尔吉侬的花束
- 2.2.2 走迷宫
- 2.2.3 八数码
- 2.2.4 地牢大师
- 2.3 Flood Fill
-
- 2.3.1 池塘计数
- 2.3.2 城堡问题
- 2.3.3 山峰和山谷
- 2.4 最短路模型
-
- 2.4.1 迷宫问题
- 2.4.2 武士风度的牛
- 2.4.3 抓住那头牛
- 2.5 多源BFS
-
- 2.5.1 矩阵距离
- 2.6 最小步数模型
-
- 2.6.1 魔板
- 2.7 双端队列广搜
-
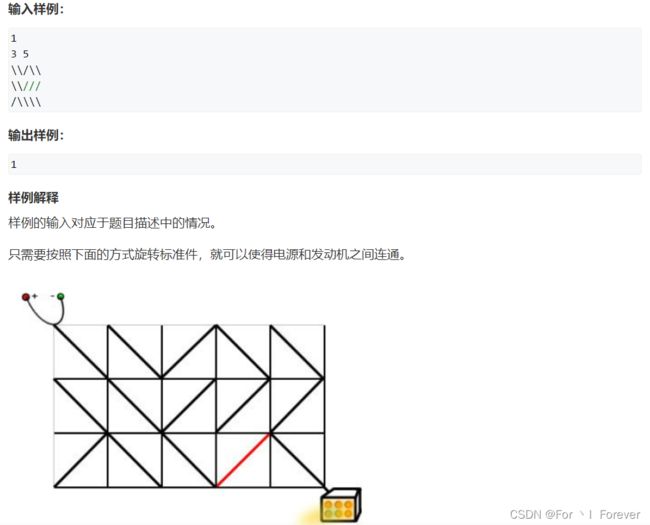
- 2.7.1 电路维修(待补充)
- 2.8 双向广搜(待补充)
-
- 2.8.1 字串变换
- 2.9 A-star
-
- 2.9.1 第k短路
- 2.9.2 八数码
- 三、递推与递归
-
- 3.1 基本思想
- 3.2 基础题目
-
- 3.2.1 递归实现指数型枚举
- 3.2.2 递归实现排列型枚举
- 3.2.3 递归实现组合型枚举
- 3.2.4 带分数
- 四、图论
时间复杂度介绍
一般ACM或者笔试题的时间限制是1秒或2秒。
在这种情况下，C++代码中的操作次数控制在 1 0 7 ∼ 1 0 8 10^7∼10^8 107∼108 为最佳。
下面给出在不同数据范围下，代码的时间复杂度和算法该如何选择：
- n ≤ 30 n≤30 n≤30,
指数级别, dfs+剪枝，状态压缩dp - n ≤ 100 n≤100 n≤100 => O ( n 3 ) O(n^3) O(n3)，
floyd，dp，高斯消元 - n ≤ 1000 n≤1000 n≤1000 => O ( n 2 ) O(n^2) O(n2)， O ( n 2 l o g n ) O(n^2logn) O(n2logn)，
dp，二分，朴素版Dijkstra、朴素版Prim、Bellman-Ford - n ≤ 10000 n≤10000 n≤10000 => O ( n ∗ n ) O(n∗\sqrt{n}) O(n∗n)，
块状链表、分块、莫队 - n ≤ 100000 n≤100000 n≤100000 => O ( n l o g n ) O(nlogn) O(nlogn) =>
各种sort，线段树、树状数组、set/map、heap、拓扑排序、dijkstra+heap、prim+heap、Kruskal、spfa、求凸包、求半平面交、二分、CDQ分治、整体二分、后缀数组、树链剖分、动态树 - n ≤ 1000000 n≤1000000 n≤1000000 => O ( n ) O(n) O(n), 以及常数较小的 O ( n l o g n ) O(nlogn) O(nlogn) 算法 =>
单调队列、 hash、双指针扫描、并查集，kmp、AC自动机，常数比较小的 O ( n l o g n ) O(nlogn) O(nlogn) 的做法：sort、树状数组、heap、dijkstra、spfa - n≤10000000n≤10000000 => O(n)O(n)，
双指针扫描、kmp、AC自动机、线性筛素数 - n ≤ 1 0 9 n≤10^9 n≤109 => O ( n ) O(\sqrt{n}) O(n)，
判断质数 - n ≤ 1 0 18 n≤10^{18} n≤1018 => O ( l o g n ) O(logn) O(logn)，
最大公约数，快速幂，数位DP - n ≤ 1 0 1000 n≤10^{1000} n≤101000 => O ( ( l o g n ) 2 ) O((logn)^2) O((logn)2)，
高精度加减乘除 - n ≤ 1 0 100000 n≤10^{100000} n≤10100000 => O ( l o g k × l o g l o g k ) O(logk×loglogk) O(logk×loglogk)，
k表示位数，高精度加减、FFT/NTT int数据范围：-2147483648~2147483647、大约 2 ∗ 1 0 9 2*10^9 2∗109左右long long数据范围：正负 1 0 18 10^{18} 1018之间- 输入的数据范围 ＜ 1 0 5 ＜10^5 ＜105，可以用
cin、cout - 输入的数据范围 ≥ 1 0 5 ≥10^5 ≥105，建议用
scanf、printf - 2 16 ≈ 1 0 6 2^{16}≈10^6 216≈106、 2 16 = 65536 2^{16}=65536 216=65536、 2 63 ≈ 1 0 18 2^{63}≈10^{18} 263≈1018
前言
队列，bfs。栈，dfs，递归。
《深入理解计算机系统》
bfs： 数据结构：queue、空间：O(2^h)空间大、可以找到一条合法路径，最小步数，一层一层进行拓展，最短路。
dfs： 数据结构：stack、空间：O(n)空间小、不能找最短路径，不具有最短路性质
思路奇怪的：dfs
最短距离：bfs
技巧：
4方向偏移量：
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
8方向偏移量：
int dx[8] = {-1, -1, -1, 0, 1, 1, 1, 0};
int dy[8] = {-1, 0, 1, 1, 1, 0, -1, -1};
8方向日字形偏移量：
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
注意： 对于多组输入的题目，不要忘记将判重数组初始化memset
深搜注意爆栈
深搜恢复现场：一个状态需要多次使用时才会恢复现场。
一、深搜
回溯、剪枝
1.1 深搜思想
关键：考虑顺序，遍历全部方案。
回溯时恢复现场st[]数组
path[]存路径
Flood Fill、图与树的遍历、
深搜的返回条件
//迷宫问题：是否走到最后一个点
if(x==xb&&y==yb) return true;
//其他类搜索问题：是否搜索到最后一个点
if(cnt==n*m) {ans++;return;}
//搜索到没有解
cnt+=dfs(a,b);
1.2 基础题目
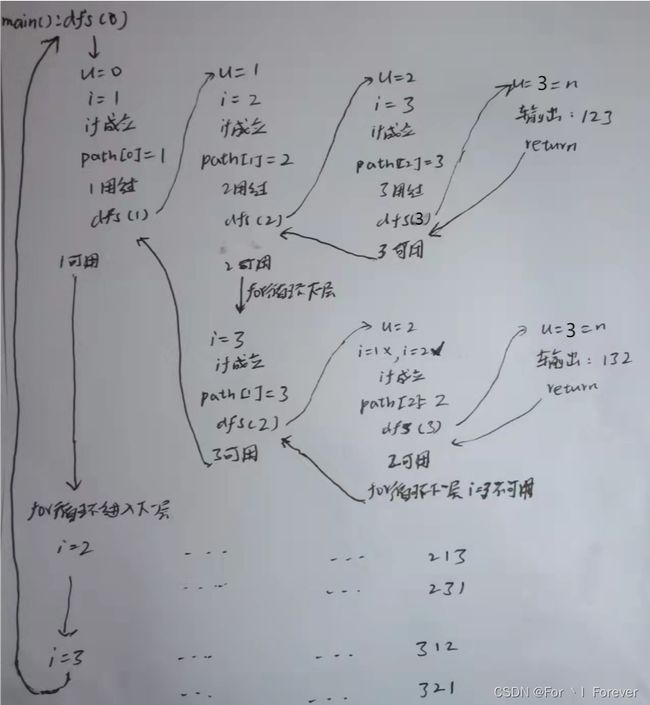
1.2.1 排列数字
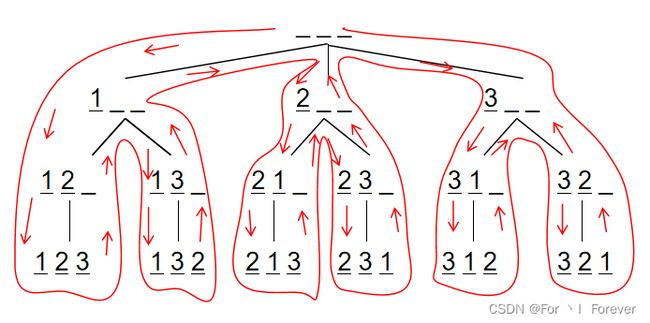
假设有 3 个空位，从前往后填数字，每次填一个位置，填的数字不能和前面一样。
最开始的时候，三个空位都是空的：__ __ __
首先填写第一个空位，第一个空位可以填 1，填写后为：1 __ __
填好第一个空位，填第二个空位，第二个空位可以填 2，填写后为：1 2 __
填好第二个空位，填第三个空位，第三个空位可以填 3，填写后为： 1 2 3
这时候，空位填完，无法继续填数，所以这是一种方案，输出。
然后往后退一步，退到了状态：1 2 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 3 ，没有其他数字可以填。
因此再往后退一步，退到了状态：1 __ __。第二个空位上除了填过的 2，还可以填 3。第二个空位上填写 3，填写后为：1 3 __
填好第二个空位，填第三个空位，第三个空位可以填 2，填写后为： 1 3 2
这时候，空位填完，无法继续填数，所以这是一种方案，输出。
然后往后退一步，退到了状态：1 3 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 2，没有其他数字可以填。
因此再往后退一步，退到了状态：1 __ __。第二个空位上除了填过的 2，3，没有其他数字可以填。
因此再往后退一步，退到了状态：__ __ __。第一个空位上除了填过的 1，还可以填 2。第一个空位上填写 2，填写后为：2 __ __
填好第一个空位，填第二个空位，第二个空位可以填 1，填写后为：2 1 __
填好第二个空位，填第三个空位，第三个空位可以填 3，填写后为：2 1 3
这时候，空位填完，无法继续填数，所以这是一种方案，输出。
然后往后退一步，退到了状态：2 1 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 3，没有其他数字可以填。
因此再往后退一步，退到了状态：2 __ __。第二个空位上除了填过的 1，还可以填 3。第二个空位上填写 3，填写后为：2 3 __
填好第二个空位，填第三个空位，第三个空位可以填 1，填写后为：2 3 1
这时候，空位填完，无法继续填数，所以这是一种方案，输出。
然后往后退一步，退到了状态：2 3 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 1，没有其他数字可以填。
因此再往后退一步，退到了状态：2 __ __。第二个空位上除了填过的 1，3，没有其他数字可以填。
因此再往后退一步，退到了状态：__ __ __。第一个空位上除了填过的 1，2，还可以填 3。第一个空位上填写 3，填写后为：3 __ __
填好第一个空位，填第二个空位，第二个空位可以填 1，填写后为：3 1 __
填好第二个空位，填第三个空位，第三个空位可以填 2，填写后为：3 1 2
这时候，空位填完，无法继续填数，所以这是一种方案，输出。
然后往后退一步，退到了状态：3 1 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 2，没有其他数字可以填。
因此再往后退一步，退到了状态：3 __ __。第二个空位上除了填过的 1，还可以填 2。第二个空位上填写 2，填写后为：3 2 __
填好第二个空位，填第三个空位，第三个空位可以填 1，填写后为：3 2 1
这时候，空位填完，无法继续填数，所以这是一种方案，输出。
然后往后退一步，退到了状态：3 2 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 1，2，没有其他数字可以填。
因此再往后退一步，退到了状态：3 __ __。第二个空位上除了填过的 1，2，没有其他数字可以填。
因此再往后退一步，退到了状态：__ __ __。第一个空位上除了填过的 1，2，3，没有其他数字可以填。
此时深度优先搜索结束，输出了所有的方案。
算法：
- 用 path 数组保存排列，当排列的长度为 n 时，是一种方案，输出。
- 用 state 数组表示数字是否用过。当 state[i] 为 1 时：i 已经被用过，state[i] 为 0 时，i 没有被用过。
- dfs(i) 表示的含义是：在 path[i] 处填写数字，然后递归的在下一个位置填写数字。
- 回溯：第 i 个位置填写某个数字的所有情况都遍历后， 第 i 个位置填写下一个数字。
代码：
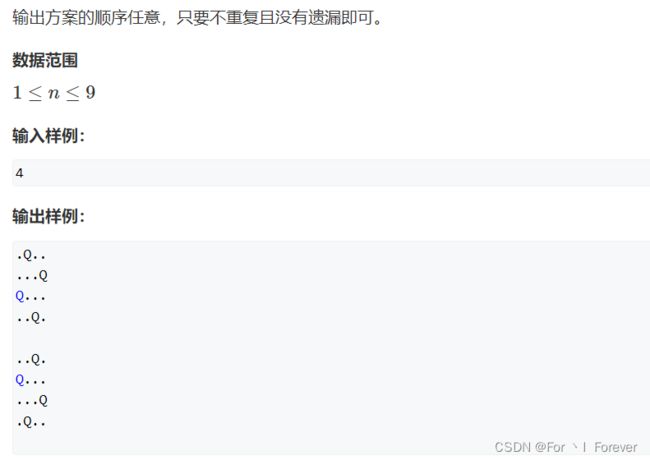
#include 1.2.2 n-皇后问题
DFS按行枚举
对角线 dg[u+i]，反对角线udg[n−u+i]中的下标 u+i和 n−u+i表示的是截距
下面分析中的(x,y)相当于上面的(u,i)
- 反对角线
y=x+b, 截距b=y−x，因为我们要把b当做数组下标来用，显然 b 不能是负的，所以我们加上+n（实际上+n+4,+2n都行），来保证是结果是正的，即y - x + n - 对角线
y=−x+b, 截距是b=y+x，这里截距一定是正的，所以不需要加偏移量
核心目的： 找一些合法的下标来表示dg或udg是否被标记过，所以如果你愿意，你取 udg[n+n−u+i] 也可以，只要所有(u,i)对可以映射过去就行
代码：
#include DFS按每个元素枚举
每个位置都有两种情况，总共有 n^2 个位置
代码：
#include 1.3 DFS中的连通性(能走到，不能保证最短)DFS、BFS均可以求解
1.3.1 迷宫
算法思想：
只能保证搜到，不能保证最短。
相对BFS，DFS(用系统栈)代码短一些。
代码：
#include 1.3.2 红与黑
算法思想：
每一个格子只会被搜一次，不需要恢复现场。
若将整个棋盘当成一个状态，进行一次染色，需要恢复现场。
关键：一个状态需要多次使用时才会恢复现场。
深搜代码：
#include 1.宽搜代码：
#include 1.4 DFS中的搜索顺序
想一个搜索顺序，将所有情况搜索到。
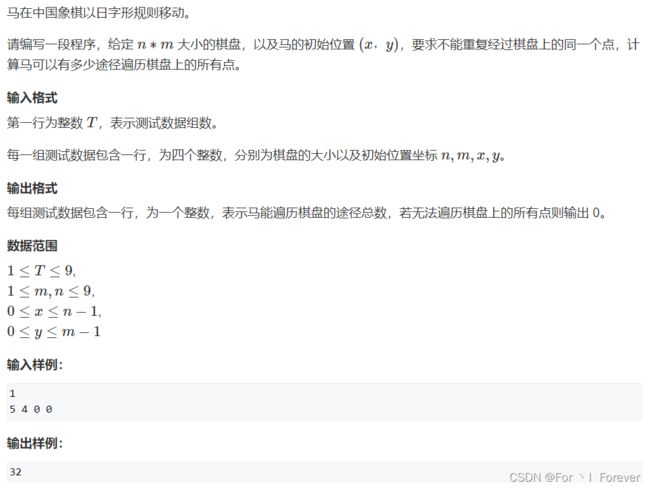
1.4.1 马走日
算法思想：
注意：恢复现场
代码：
#include 1.4.2 单词接龙
算法思想：
首先枚举以给定字母开头的单词，对于每个单词分别向下递归搜索，每次枚举可以接在后面的所有单词，直到不能搜为止，计算长度最大值。
代码：
#include 1.4.3 分成互质组(待补充)
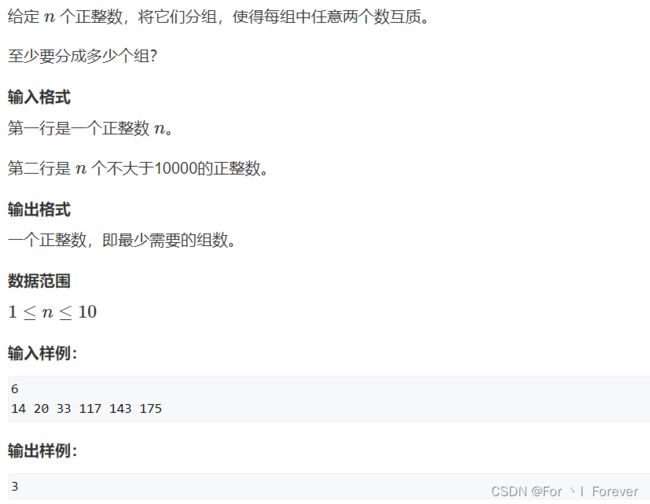
算法思想：
如果两个数互质，连一条边，表示有关系。将图中的点最少分成多少组，可以使得每一组内没有边。转化为图论。
代码：
1.5 DFS剪枝
未来不是我们想要的，可以提前退出搜索，提高搜索效率。
常见的剪枝策略：
1.优化搜索顺序，大部分情况下，我们应该优先搜索分支较少的节点。
2.排除等效冗余。不考虑的情况下，用组合的方式进行搜索。
3.可行性剪枝
4.最优性剪枝
5.记忆化搜索(DP)
1.5.1 小猫爬山
算法思想：
代码：
1.5.2 数独
二、宽搜
每次取出队头元素，将该元素拓展出的所有元素放到队尾。取出的顺序是层次遍历的顺序，加入的顺序也是层次遍历的顺序。
当一个图中所有边的权重为1，可以考虑用宽搜
BFS： 求最小/最短，基于迭代的算法，不会爆栈。
数据结构：判重数组st[ ] (入队时判重，出队时判重)，queue
2.0 宽搜模板
//宽搜框架
//二维 typedef pair PII; #define x first PII start,end;
//三维 struct Point{int x,y,z;};
queue<-初始状态
queue<PII> q;q.push(start);
int hh=0,tt=0;q[0]=start;q[0]={0,0};
//dist[]数组初始化
memset(dist,-1,sizeof dist);
dist[start.x][start.y]=0;
//判重数组初始化
st[0][0]=true;
st[start.x][start.y]=true;//表明该数已经用过
//一些多组输入的题目，需要进行初始化操作
memset(st,false,sizeof st);
while(queue非空)//q.size() hh<=tt
{
t<-队头//auto t=q.front();q.pop(); auto t=q[hh++];
//定义方向，二维dx、dy，三维dx、dy、dz
for(拓展t)//int i=0;i<4/6;i++
{
var<-t拓展的新节点
//int x=t.x+dx[i],y=t.y+dy[i];
if(!st[var])
var->队尾
//判断
if(是否在范围内&&dist[x][y]==-1&&g[x][y]!='#') 未拓展且不是障碍
//更新dist
dist[x][y]=dist[t.x][t.y]+1;
//判断是否结束
if(g[x][y]=='E') return dist[x][y];
if(end==make_pair(x,y)) return dist[x][y];
if(x==end.x&&y==end.y&&z==end.z) return dist[x][y][z];
//拓展新的节点
q.push({x,y}) q[++tt]={x,y};
}
}
//return -1;
常见的题型
求最短距离，引入dist[][]，初始化为-1，起点的dist值为0，当满足条件时，将dist[a][b]=dist[t.x][t.y]+1，并判断是否到达终点，返回dist[a][b]
dist[][]作用：一般初始化为-1。既可以判重，又可以记录答案，即距离。
Flood Fill，引入判重数组st[][]，将扫描的点设置为st[][]=true，进行条件判断若!st[a][b]，还没有扫描，执行相应的操作，并设置st[a][b]=true
2.1 宽搜类型
- 最短距离： 走迷宫，每一个格子是一个点，即每个格子是一个状态。在一个地图种，给定一个起点、终点，从起点走到重点的最短距离。
- 最小步数： 矩阵/棋盘，八数码问题，整个是一个状态，每次枚举能变成什么状态。从一个地图到另一个地图。
2.2 基础题目
2.2.1 献给阿尔吉侬的花束
用a[N][N]接收地图，dist[N][N]存储到每个点的路径长度。
从起点出发，广度优先遍历地图：
- 起点入队。
- 如果队列非空，一直执行下面语句：
队头出队。
遍历队头的上下左右四个方向：如果是 ‘.’ 走过去，并且该位置入队，该点对应的dis值更新为队头的dis + 1，该点更新为’#’,表示走过了。如果是 ‘#’ 不做处理，如果是 ‘E’,走到了终点，输出该点对应的 dis 值。 - 如果队列为空，还没有找到终点，则无法到达，输出 oop!。
代码：
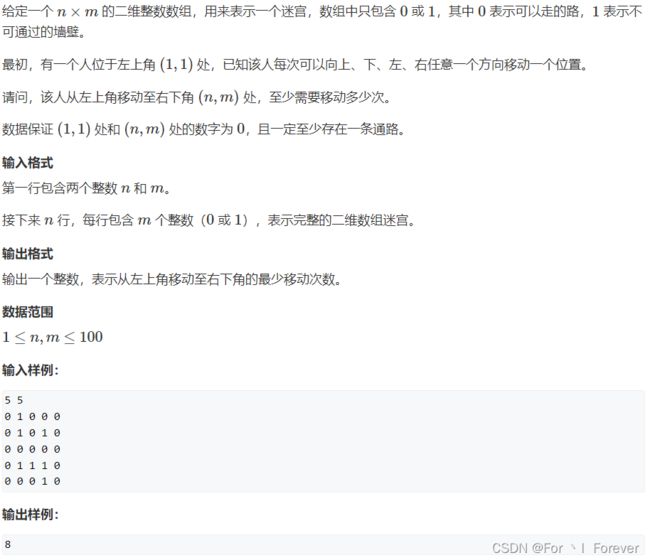
#include 2.2.2 走迷宫
代码：
#include 输出路径
2.2.3 八数码
2.2.4 地牢大师
二维拓展为三维：
沿着x轴前进：1,0,0
沿着x轴后退：-1,0,0
沿着y轴前进：0,1,0
沿着y轴后退：0,-1,0
沿着z轴前进：0,0,1
沿着z轴后退：0,0,-1
代码：
#include 2.3 Flood Fill
从一个起点开始，每一次选择一个新加进来的格子，直到不能拓展新的格子为止。
可以在线性时间复杂度内，找到某个点所在的连通块。
2.3.1 池塘计数
算法思想：
遍历每一个格子，对于当前格子如果是水，即W，进行cnt++，执行flood fill。
需要注意的在st[x][y]=true，表示将该点放到判重数组，为1表示已经用过。
代码：
#include 2.3.2 城堡问题
算法思想：
注意：area++的位置。
代码：
#include 2.3.3 山峰和山谷
算法思想：
往外进行拓展的时候，判断一下拓展的格子是否属于连通块，并统计两者之间的关系
找到高度一致的连通块，若该连通块周围
- 没有存在比它高的则该连通块叫山峰
- 没有存在比它矮的则该连通块叫山谷
统计连通块(边界)与其相邻节点的关系：
- 在入队时判断相邻点是否属于当前联通块, 若不属于则判断高度关系.
- 实现时, 只需要判断是否存在有低于/高于当前节点的相邻点即可.
代码：
#include 2.4 最短路模型
2.4.1 迷宫问题
算法思想：
宽搜记录路径
PII类型的pre[][]数组即用来判重标记，又存储当前路径
代码：
#include 用st[][]数组进行标记
#include 2.4.2 武士风度的牛
算法思想：
本题的求解，
代码：
#include 2.4.3 抓住那头牛
算法思想：
可以用宽搜：可以看成边的权重均为1
代码：
#include q;q.push(n);
int hh=0,tt=0;
while(hh<=tt)
{
int t=q[hh++];//int t=q.front();q.pop();
if(t==k) return dist[k];
if(t+1<N && dist[t+1]==-1)
{
dist[t+1]=dist[t]+1;
q[++tt]=t+1;//q.push(t+1);
}
if(t-1>=0&& dist[t-1]==-1)
{
dist[t-1]=dist[t]+1;
q[++tt]=t-1;
}
if(t*2<N&& dist[2*t]==-1)
{
dist[2*t]=dist[t]+1;
q[++tt]=2*t;
}
}
return -1;
}
int main()
{
cin >> n >> k;
cout << bfs() << endl;
return 0;
}
2.5 多源BFS
2.5.1 矩阵距离
算法思想：
有很多起点，每次求出某点到离它最近的起点的距离。
代码：
#include 2.6 最小步数模型
2.6.1 魔板
算法思想：
有向图中的最短距离
1.如何存储状态？ 哈希存储。康拓展开
map、unordered-map
将答案1、2、3、4、5、6、7、8放到队列队头，用宽搜搜索所有的状态，直到搜到终点为止。每次拓展时，进行A、B、C三种操作，得到一个字符串判断是否搜到过，未搜，存队列。
2.如何存方案？ 存储每一个状态由哪个状态转移过来的。终点->起点
3.如何得到字典序最小的操作？ 往队列插的时候，按照先A再B再C的顺序插入，一定可以得到一个最小字典序的答案。
代码：
#include 2.7 双端队列广搜
2.7.1 电路维修(待补充)
算法思想：
只包含0和1两种边权的最短路问题
与一般的BFS的差别： 如果拓展出来的边的权重是0，插入到队头，拓展出来的边的权重是1，插入到队尾。
解决问题：
双端队列主要解决图中边的权值只有0或者1的最短路问题
操作：
每次从队头取出元素，并进行拓展其他元素时
- 若拓展某一元素的边权是
0，则将该元素插入到队头 - 若拓展某一元素的边权是
1，则将该元素插入到队尾
与堆优化Dijkstra 一样，必须在出队时才知道每个点最终的最小值，而和一般的bfs不一样，原因是如下图所示
首先明确的一点是，这里是图中的格子和点是不一样的，点是格子上的角角上的点，每个点都有4个方向可以走，分别对应的是左上角，右上角，右下角，左下角，
踩过格子到达想去的点时，需要判断是否需要旋转电线，若旋转电线表示从 当前点 到 想去的点 的边权是1，若不旋转电线则边权是0
按左上角，右上角，右下角，左下角遍历的顺序
dx[]和dy[]表示可以去其他点的方向id[]和iy[]表示需要踩某个方向的各种才能去到相应的点cs[]表示当前点走到4个方向的点理想状态下格子形状(边权是0的状态)
代码：
2.8 双向广搜(待补充)
2.8.1 字串变换
2.9 A-star
2.9.1 第k短路
2.9.2 八数码
三、递推与递归
3.1 基本思想
递归，自己调用自己。
所有递归都可以转化为一个递归搜索树
求斐波那契数列， f ( n ) = f ( n − 1 ) + f ( n − 2 ) ， ( n ≥ 3 ) f(n)=f(n-1)+f(n-2)，(n≥3) f(n)=f(n−1)+f(n−2)，(n≥3)
//实现斐波那契额数列
int fun(int n)
{
if(n==1) return 1;
if(n==2) return 2;
else return f(n-1)+f(n-2);
}
3.2 基础题目
3.2.1 递归实现指数型枚举
算法思想：
递归，dfs，最重要的是顺序。从1~n依次考虑每个数选或者不选。
代码：
#include STL的做法代码：
#include3.2.2 递归实现排列型枚举
算法思想：
顺序1：依次枚举每个数放到哪个位置
顺序2：依次枚举每个位置放哪个数
代码：
#include 3.2.3 递归实现组合型枚举
算法思想：
在排列型枚举的基础上加一些限定，局部考虑，只需要保证每次新加的数大于前一个数。
- 存放三个位置的数据结构，path[][]数组
- 当前枚举哪个位置，u
- start当前最小可以从哪个数枚举
代码：
#include 动态数组做法代码：
#include3.2.4 带分数
算法思想：
递归枚举全排列
枚举a、b的位数
判断等式是否成立
代码：
四、图论
有向图、无向图
有向图的存储：
邻接矩阵(用的少，二维数组g[a][b])、邻接表(用的多，单链表)