算法很美 笔记 7.深入递归,深搜,回溯,剪枝等
7.深入递归,深搜,回溯,剪枝等
"逐步生成结果”类问题之数值型
-
自下而上的递归(递推,数学归纳,动态规划)
- 解决简单情况下的问题
- 推广到稍复杂情况下的问题.
- 如果递推次数很明确,用迭代
- 如果有封闭形式,可以直接求解
题1:三步问题
三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。
示例1:
输入:n = 3
输出:4
说明: 有四种走法
示例2:
输入:n = 5
输出:13
提示:
n范围在[1, 1000000]之间
思考一下这个问题:最后一次小孩迈了几步?
小孩上楼梯的最后一步,就是抵达第n 阶的那一步,迈过的台阶数可以是3、2 或者1。
那么小孩有多少种方法走到第n 阶台阶呢?目前还不知道,但我们可以把它与一些子问题联系起来。
到第n 阶台阶的所有路径,可以建立在前面3 步路径的基础之上。我们可以通过以下任意方式走到第n 阶台阶。
在第n-1 处往上迈1 步。
在第n-2 处往上迈2 步。
在第n-3 处往上迈3 步。
因此,我们只需把这3 种方式的路径数相加即可。
这里要非常小心,有很多人会把它们相乘。相乘应该是走完一个再走另一个,显然和以上
情况不符。
public static int waysToStep(int n) {
if(n==1){
return 1;
}else if(n==2){
return 2;
}else if(n==3){
return 4;
}else{
return waysToStep(n-1)+waysToStep(n-2)+waysToStep(n-3);
}
}
public static int waysToStep2(int n) {
if(n==1){
return 1;
}else if(n==2){
return 2;
}else if(n==3){
return 4;
}else{
int x1=1;
int x2=2;
int x3=4;
int m=1000000007;
for (int i = 0; i < n-3; i++) {//大于3时,为前3个和
int t=x1;//因为下面赋值要覆盖x1,备份下
//对x1、x2、x3进行更新
x1=x2;
x2=x3;
x3=((x1+x2)%m+t)%m;//新x3=旧x1+旧x2+旧x3
}
return x3;
}
}
题目链接
题2:机器人走方格
有一个XxY的网格,一个机器人只能走格点且只能向右或向下走,要从左上角走到右下角。请设计一个算法,计算机器人有多少种走法。
给定两个正整数int x,int y,请返回机器人的走法数目。保证x+y小于等于12。
测试样例:
2,2
返回:2
先不断在小范围内发现规律,在求解新问题时尽可能用到原来求的,得到新问题的答案
| x=y=1 | 1 |
|---|---|
| x=1 y=2 | 1 |
| x=2 y=1 | 1 |
| x=2 y=2 | 1+1=2 分解为向右走一步(x=1 y=2)+向下走一步(x=2 y=1) |
| x=3 y=2 | 1+2=3 分解为向右走一步(x=3 y=1)+向下走一步(x=2 y=2) |
| x=2 y=3 | 1+2=3 分解为向右走一步(x=2 y=2)+向下走一步(x=1 y=3) |
| x=3 y=3 | 3+3=6 分解为向右走一步(x=3 y=2)+向下走一步(x=2 y=3) |
| 1 | 1 | 1 |
|---|---|---|
| 1 | 2 | 3 |
| 1 | 3 | 6 |
第一行和第一列都是1,a[i][j]=a[i-1][j]+a[i][j-1]
public static int countWays(int x, int y) {
int[][] a=new int[x+1][y+1];
for (int i = 1; i <=x; i++) {
a[i][1]=1;
}
for (int i = 1; i <=y; i++) {
a[1][i]=1;
}
for (int i = 2; i <=x ; i++) {
for (int j = 2; j <=y ; j++) {
a[i][j]=a[i-1][j]+a[i][j-1];
}
}
return a[x][y];
}
题目链接
题3:硬币
硬币。给定数量不限的硬币,币值为25分、10分、5分和1分,编写代码计算n分有几种表示法。(结果可能会很大,你需要将结果模上1000000007)
示例1:
输入: n = 5
输出:2
解释: 有两种方式可以凑成总金额:
5=5
5=1+1+1+1+1
示例2:
输入: n = 10
输出:4
解释: 有四种方式可以凑成总金额:
10=10
10=5+5
10=5+1+1+1+1+1
10=1+1+1+1+1+1+1+1+1+1
说明:
注意:
你可以假设:
0 <= n (总金额) <= 1000000
final static int[] coin ={1,5,10,25};
public static int waysToChange(int n) {
return makeChange(n,3);
}
public static int makeChange(int amount,int index){//amount表示金额,coin[index]为最大使用面值
if (index==0){
return 1;
}
int sum=0;
for (int i = 0; i*coin[index] <=amount ; i++) {//i为使用最大面值的数量0,1,2,3
sum+= makeChange(amount-i*coin[index],index-1);
}
return sum;
}
public static int waysToChange2(int n) {
final int md=1000000007;
int[] coin={1,5,10,25};
int[][] a=new int[4][n+1];
for (int i = 0; i < 4; i++) {
a[i][0]=1;
}
for (int i = 0; i < n+1; i++) {
a[0][i]=1;
}
for (int i = 1 ; i <4 ; i++) {//i为可以使用的最大面值
for (int j = 1; j <n+1 ; j++) {//j为要凑得数
for (int k = 0; k*coin[i]<=j ; k++) {//k为当前可使用的最大面值的数量
a[i][j]=(a[i][j]+a[i-1][j-k*coin[i]])%md;
//例如25 100,表示用最大25的去凑100,25的数量为k为0,1,2,3,4,已经确定了面值25的数量,需要确定最大能使用10面值的数量为i-1
//剩余金额为j-k*coin[i],此处结果为a 10 100,a 10 75,a 10 50,a 10 25,a 10 0
}
}
}
return a[3][n];
}
public static int waysToChange3(int n) {
final int md=1000000007;
int[] coin={1,5,10,25};
int[] a=new int[n+1];
a[0]=1;//不使用任何硬币,表示0元有一种方法
for (int i = 0; i < 4; i++) {//使用新面值coin[i],1~n钱数的方法总数
for (int j = coin[i]; j <n+1; j++) {//增加新面值后,方法总数受影响的是从coin[i]开始的
a[j]=(a[j]+a[j-coin[i]])%md;
//方法总数=使用新的面值方法总数((j-面值)的方法总数)+不使用新面值的方法总数(为原来值)
}
}
return a[n];
}
题目链接
"逐步生成结果”类问题之非数值型
- 此时就要用容器去装了
- 生成一点,装一点,所谓迭代就是慢慢改变
题3:括号
括号。设计一种算法,打印n对括号的所有合法的(例如,开闭一一对应)组合。
说明:解集不能包含重复的子集。
例如,给出 n = 3,生成结果为:
[ “((()))”,
“(()())”,
“(())()”,
“()(())”,
“()()()”]
看到这个题,可能我们的第一反应是用递归法,在f(n-1)答案的基础上加一对括号,从而
得到f(n)的解答。从直觉上看,这个方法不错。
下面来看看n = 3 时的答案:
(()()) ((())) ()(()) (())() ()()()
如何以n = 2 时的答案为基础构建上面的结果呢?
(()) ()()
我们可以在字符串最前面以及原有的每对括号里面插入一对括号。至于插入其他任意位置,
比如字符串的末尾,都会跟之前的情况重复。
综上所述,可得到以下结果。
(()) -> (()()) 在第1 个左括号之后插入一对括号
-> ((())) 在第2 个左括号之后插入一对括号
-> ()(()) 在字符串开头插入一对括号
()() -> (())() 在第1 个左括号之后插入一对括号
-> ()(()) 在第2 个左括号之后插入一对括号
-> ()()() 在字符串开头插入一对括号
且慢,上面有重复的括号对组合,()(())出现了两次。
如果准备采用这种做法,那么,将字符串放进结果列表之前,必须先检查有无重复值。
public static Set<String> Parenthesis(int n){
Set<String> newRes=new HashSet<String>();
if(n==1){
newRes.add("()");
return newRes;
}
Set<String> res=Parenthesis(n-1);
for (String s:res) {
for (int i = 0; i <s.length() ; i++) {
if(s.charAt(i)=='('){
newRes.add(s.substring(0,i+1)+"()"+s.substring(i+1,s.length()));
}
newRes.add("()"+s);
}
}
return newRes;
}
public static List<String> generateParenthesis(int n) {
Set<String> res=Parenthesis(n);
List<String> list=new LinkedList<String>();
for (String s:res) {
list.add(s);
}
return list;
}
题目链接
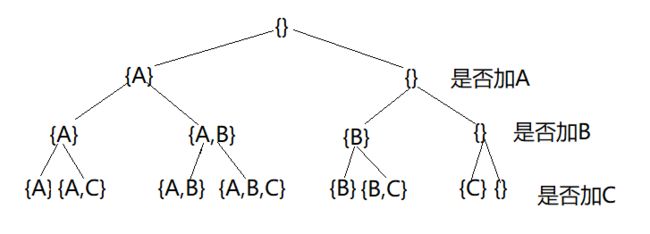
题3:幂集
幂集。编写一种方法,返回某集合的所有子集。集合中不包含重复的元素。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]]
/*逐步生成迭代大法*/
public Set<Set<Integer>> getSubsets2(int[] A, int n) {
Set<Set<Integer>> res = new HashSet<>();
res.add(new HashSet<>());//初始化为空集
//从第一个元素开始处理
for (int i = 0; i < n; i++) {
Set<Set<Integer>> res_new = new HashSet<>();//新建一个大集合
res_new.addAll(res);//把原来集合中的每个子集都加入到新集合中
//遍历之前的集合,全部克隆一遍
for (Set e : res) {
Set clone = (Set) ((HashSet) e).clone();
clone.add(A[i]);//把当前元素加进去
res_new.add(clone);//把克隆的子集加到大集合中
}
res = res_new;
}
return res;
}
/**
* 增量构造法
* @param A
* @param n
* @return
*/
public Set<Set<Integer>> getSubsets3(int[] A, int n) {
// Arrays.sort(A);
return getSubsets3Core(A, n, n - 1);
}
private Set<Set<Integer>> getSubsets3Core(int[] A, int n, int cur) {
Set<Set<Integer>> newSet = new HashSet<>();
if (cur == 0) {//处理第一个元素
Set<Integer> nil = new HashSet<>();//空集
Set<Integer> first = new HashSet<>();//包含第一个元素的集合
first.add(A[0]);
newSet.add(nil);
newSet.add(first);
return newSet;
}
Set<Set<Integer>> oldSet = getSubsets3Core(A, n, cur - 1);
for (Set<Integer> set : oldSet) {
//对于每个子集,cur这个元素可以加进去,也可以不加进去
newSet.add(set);//保留原样
Set<Integer> clone = (Set<Integer>) ((HashSet) set).clone();
clone.add(A[cur]);//添加当前元素
newSet.add(clone);
}
return newSet;
}
1 2 3
3 2 1
111 321
110 32
101 31
100 3
011 21
010 2
001 1
000 【】
public static List<List<Integer>> subsets(int[] nums) {//二进制的方法
Arrays.sort(nums);
List<List<Integer>> res=new ArrayList<List<Integer>>();
for (int i =(int)Math.pow(2,nums.length)-1; i>=0 ; i--) {//从大的数字到小的数字
List<Integer> n=new ArrayList<Integer>();
for (int j=nums.length-1;j>=0;j--) {//j为右移位数,从num.length-1到0
if(((i>>j)&1)==1){//从高位到低位判断是否为1
n.add(nums[j]);//从右往左填入数字
}
}
res.add(n);
}
return res;
}
题目链接
题4:全排列
给定一个没有重复数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[ [1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]]
题目链接
方法1:
如果有n个元素,全排列数量等于n!
-
A 第一次为一个元素
-
BA AB 往A的前后插 (在上步*2)
-
CBA BCA BAC 往BA前、中、后插入 CAB ABC ABC 往AB前、中、后插入 (在上步*3)
最后一步得到结果
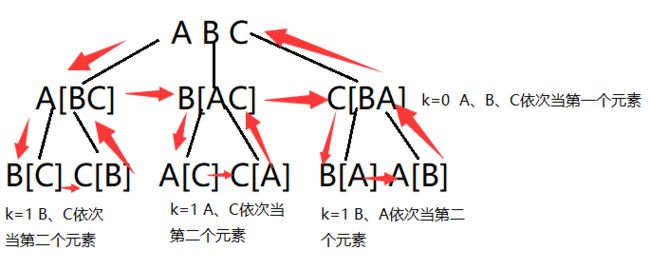
方法2:交换使不同元素当第K位
交换
递归
回溯
无法维持字典序,只是输出用这个方法
递归先走到底才回溯,到离自己最近的兄弟,继续到底再回溯
static List<List<Integer>> res;
public static List<List<Integer>> permute(int[] nums) {
res=new ArrayList<List<Integer>>();
Arrays.sort(nums);
getPermutationCore(nums,0);///以0基准,0及其以后的依次当第一个元素
return res;
}
public static void swap(int[] l,int i,int j){
int t=l[i];
l[i]=l[j];
l[j]=t;
}
public static void getPermutationCore(int[] list,int k){
if(k==list.length){//排好了一种情况,递归的支路走到底了
Integer[] integers=new Integer[list.length];
for (int i = 0; i < list.length; i++) {
integers[i]=list[i];
}
res.add(Arrays.asList(integers));
}
for (int i = k; i < list.length; i++) {//k是基准,k及其以后的依次换到k这里。当第k个元素
swap(list,i,k);
getPermutationCore(list,k+1);//k+1为基准
swap(list,i,k);//回溯,由于是对同一数组操作,恢复原样
}
}
方法3:前缀法
初始是一个筐,每次选没有的入围,判断标准:筐里这个字符数量小于字符集这个元素的数量
可以维持字典序,需要求第K个,要用这个方法
//调用permutation(字符串(有序且字符不能重复),第几个)
static int count=0,k;
static String s;
public static void permutation(String s1,int k1){
count=0;
k=k1;
s=s1;
permutation("");
}
public static void permutation(String pat){
if (count==k){
return;
}
if(pat.length()==s.length()){//前缀的长度==字符集的长度,一个排列就完成了
count++;
if(count==k){
System.out.println(pat);
return;
}
return;
}
//每次都从头扫描,只要该字符可用,我们就附加到前缀后面,前缀变长了
for (int i = 0; i < s.length(); i++) {
char ch=s.charAt(i);
if(!pat.contains(ch+"")){//当前元素不在pat中
permutation(pat+ch+"");//加入这个ch,递归
}
}
}
题1:第K个排列
给出集合 [1,2,3,…,n],其所有元素共有 n! 种排列。
按大小顺序列出所有排列情况,并一一标记,当 n = 3 时, 所有排列如下:
“123”
“132”
“213”
“231”
“312”
“321”
给定 n 和 k,返回第 k 个排列。
说明:给定 n 的范围是 [1, 9]。
给定 k 的范围是[1, n!]。
示例 1:
输入: n = 3, k = 3
输出: “213”
示例 2:
输入: n = 4, k = 9
输出: “2314”
首先考虑能不能确定第k个排列是以哪个数字开头的呢,以[1,2,3,4]的全排列为例,找第14个排列
-
以1开头的排列总共有3!个,原因是第一个位置是1,剩下3个位置可以随便排列,有6个
-
以2开头的排列总共有3!个,原因是第一个位置是2,剩下3个位置可以随便排列,有6个
-
此时已经有12个排列
-
所以剩下的两个排列即第14个排列一定在以3开头的排列中
用这种方式继续缩减数量,以3开头的排列中最小的为[3,1,2,4],3已经固定,那么就找[1,2,4]的全排列的第2个排列,就是整个排列的第14个排列
-
以1开头的排列共有2!个,原因是第二个位置是1,剩下2个位置可以随便排列,有2个
-
此时已经有两个排列,可以确定结果一定在以
[3,1]开头的排列中,即[3,1,2,4]或[3,1,4,2]
继续缩减数量,以[3,1]开头的排列中最下的为[3,1,2,4],[3,1]已经固定,那么就找[2,4]的全排列的第2个排列,就是[1,2,4]的全排列的第2个排列,也就是整个排列的第14个排列
以2开头的排列共有1!个,原因是第三个位置是2,剩下一个位置给4,有1个
以4开头的排列共有1!个,原因是第三个位置是4,剩下一个位置给12,有1个
此时已经有两个排列,可以确定结果是以4开头的排列,即[4,2],所以结果为[3,1,4,2]
所以,可以每次确定一个大范围,在大范围的基础上进一步缩小范围,直到最后只有一个数字为止。遍历n遍即可。
public static int f(int n){//求阶乘
int res=1;
for (int i = 1; i <=n ; i++) {
res=res*i;
}
return res;
}
public static String getPermutation(int n, int k) {
StringBuffer sb=new StringBuffer();
List<Integer> list=new ArrayList<Integer>();
for (int i = 1; i <=n; i++) {
list.add(i);
}
for (int i = 1;sb.length()<n ; i++) {
int interval=f(n-i);//以剩下每个元素当头,组合数未 剩下个数-1的阶乘
int num;//可以由几个interval
if(k%interval==0){
num=k/interval-1;
}else{
num=k/interval;
}
sb.append(list.get(num));//加入第 num+1个数字
list.remove(num);//除去第 num+1个数字
Collections.sort(list);//重新排序
k=k-num*interval;//剩余k
}
return sb.toString();
}
题目链接
题2:是第几个序列
已知是n = 5,求14352是它的第几个序列?(上一道题反向)
用刚才的那道题的反向思维:
第一位是1,有0个数小于1,即0* 4!
第二位是4,有2个数小于4,即2* 3!
第三位是3,有1个数小于3,即1* 2!
第四位是5,有1个数小于5,即1* 1!
第五位是2,不过不用算,因为肯定是0
所以14352是 n = 5的第 0 + 12 + 2 + 1 + 0 = 15 + 1(求的是第几个,所以要加一) = 16
封闭形式的直接解
- 汉诺塔移动次数
汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。三个盘子a到c,借助b。
| 盘子个数 | 移动次数 | 移动次数 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 3 | 3 |
| 3 | 2*3+1 | 7 |
| … | ||
| n | 2n-1 |
-
斐波那契数列第n项
[ F n F n + 1 ] = [ 0 1 1 1 ] n − 1 [ F 1 F 2 ] \left[\begin{array}{c} F_{n} & F_{n+1} \\ \end{array}\right]=\left[\begin{array}{ll} 0 & 1 \\ 1 & 1 \end{array}\right]^{n-1}\left[\begin{array}{c} F_{1} & F_{2} \\ \end{array}\right] [FnFn+1]=[0111]n−1[F1F2] -
上楼梯
一次可以上1、2、3步,n节台阶方法数
f ( n ) = [ f 1 , f 2 , f 3 ] [ 0 0 1 1 0 1 0 1 1 ] n − 3 f(n)=\left[\begin{array}{lll} f 1, & f 2, & f 3 \end{array}\right]\left[\begin{array}{lll} 0 & 0 & 1 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{array}\right]^{n-3} f(n)=[f1,f2,f3]⎣⎡010001111⎦⎤n−3
n节台阶,一次可以上1、2、3…n步,f(n)=f(1)+f(2)+f(3)+f(4)+…+f(n-1)方法数2n-1次
牢牢抓住逐步形成… !
牢牢抓住以此类推… !
深度优先搜索DFS
dfs:先把一条路走到黑
bfs:所有路口看一遍
题5:解数独
编写一个程序,通过已填充的空格来解决数独问题。
一个数独的解法需遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
空白格用 ‘.’ 表示。
一个数独。
答案被标成红色。
Note:
- 给定的数独序列只包含数字
1-9和字符'.'。 - 你可以假设给定的数独只有唯一解。
- 给定数独永远是
9x9形式的。
static boolean isFish=false;
public static boolean check(char[][] board, int x, int y, int i) {
//检查在board[x][y]填入i是否合法
for (int j = 0; j < 9; j++) {//board[x][y]所在行
if(board[x][j]=='0'+i){
return false;
}
if(board[j][y]=='0'+i){//board[x][y]所在列
return false;
}
}
//(x/3)代表第几个3组吗,(x/3+1)代表(x/3)的下一个
for (int j = (x/3)*3; j <(x/3+1)*3 ; j++) {//board[x][y]所在九宫格
for (int l = (y/3)*3; l <(y/3+1)*3 ; l++) {
if(board[j][l]=='0'+i){
return false;
}
}
}
return true;
}
public static void dfs(char[][] board,int x,int y) {
if (x==9){//填完最后一个x=8,y=8,下一个是x=9
isFish=true;
return;
}
if(board[x][y]=='.'){//当前元素没有数字
for (int i = 1; i <=9 ; i++) {//讲合法的数字填入当时空
if(check(board,x,y,i)){
board[x][y]=(char)('0'+i);//不要忘记类型转换
dfs(board,x+(y+1)/9,(y+1)%9);//递归下一个空
if(isFish){//全局变量isFish表示完成后,层层返回
return;
}
}
}
board[x][y]='.';//执行到这说明,x,y没有合适的值可以填,需要将board恢复原样,再回溯到上一次递归
}else{//有数字递归下一个空
dfs(board,x+(y+1)/9,(y+1)%9);
}
}
public static void solveSudoku(char[][] board) {
isFish=false;//由于要多次调用isFish为static,第二次调用时为上次值,要初始化
dfs(board,0,0);//board传的引用
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
System.out.print(board[i][j]+" ");
}
System.out.println();
}
}
char[][] board = new char[][]{
{'5', '3', '.', '.', '7', '.', '.', '.', '.'},
{'6', '.', '.', '1', '9', '5', '.', '.', '.'},
{'.', '9', '8', '.', '.', '.', '.', '6', '.'},
{'8', '.', '.', '.', '6', '.', '.', '.', '3'},
{'4', '.', '.', '8', '.', '3', '.', '.', '1'},
{'7', '.', '.', '.', '2', '.', '.', '.', '6'},
{'.', '6', '.', '.', '.', '.', '2', '8', '.'},
{'.', '.', '.', '4', '1', '9', '.', '.', '5'},
{'.', '.', '.', '.', '8', '.', '.', '7', '9'}
};
solveSudoku(board);
5 3 4 6 7 8 9 1 2
6 7 2 1 9 5 3 4 8
1 9 8 3 4 2 5 6 7
8 5 9 7 6 1 4 2 3
4 2 6 8 5 3 7 9 1
7 1 3 9 2 4 8 5 6
9 6 1 5 3 7 2 8 4
2 8 7 4 1 9 6 3 5
3 4 5 2 8 6 1 7 9
题目链接
题6:和恰好为k
给定整数序列a1,a2,…,an,判断是否可以从中选出若干数,使它们的和恰好为k.
1≤n≤20
-108≤ai≤108
-108≤k≤108
样例:
输入
n=4
a={1,2,4,7}
k=13
输出:
Yes
//a为数组,k为恰好为k,cur为当前元素是否要,ints为结果
private static void dfs(int[] a, int k, int cur, ArrayList<Integer> ints) {
if (k == 0) {
exit(0);
}
if (k < 0 || cur == a.length) return;
dfs(a, k, cur + 1, ints);//不要cur这个元素
ints.add(a[cur]);
int index = ints.size() - 1;
dfs(a, k - a[cur], cur + 1, ints);//要cur这个元素
ints.remove(index);//回溯
}
此题也可以用二进制法求子集的方法
题7:和为K的子数组
给定一个整数数组和一个整数 k,你需要找到该数组中和为 k 的连续的子数组的个数。
示例 1 :
输入:nums = [1,1,1], k = 2
输出: 2 , [1,1] 与 [1,1] 为两种不同的情况。
说明 :
数组的长度为 [1, 20,000]。
数组中元素的范围是 [-1000, 1000] ,且整数 k 的范围是 [-1e7, 1e7]。
public static int subarraySum(int[] nums, int k) {
int n=nums.length;
int[] sum=new int[n+1];//sum[i]用于存储 nums的序号0到i-1之间元素的和
for (int i = 1; i <=n; i++) {
sum[i]=sum[i-1]+nums[i-1];//num[1]=sum[0]+num[0]; sum[i]前i-1个元素值=前i-2个元素值+第i-1个值
}
int count=0;
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
if(sum[j+1]-sum[i]==k){//0-j的和减去0-i-1的和==i到j的和
count++;
}
}
}
return count;
}
题目链接
题8:水洼数
Descriptions:
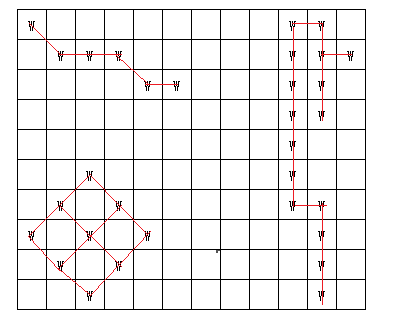
由于近日阴雨连天,约翰的农场中中积水汇聚成一个个不同的池塘,农场可以用 N x M (1 <= N <= 100; 1 <= M <= 100) 的正方形来表示。农场中的每个格子可以用’W’或者是’.'来分别代表积水或者土地,约翰想知道他的农场中有多少池塘。池塘的定义:一片相互连通的积水。任何一个正方形格子被认为和与它相邻的8个格子相连。
给你约翰农场的航拍图,确定有多少池塘
Input
Line 1: N 和 M
Lines 2…N+1: M个字符一行,每个字符代表约翰的农场的土地情况。每个字符中间不包含空格
Output
Line 1: 池塘的数量
Sample Input
10 12 W........WW. .WWW.....WWW ....WW...WW. .........WW. .........W.. ..W......W.. .W.W.....WW. W.W.W.....W. .W.W......W. ..W.......W.
Sample Output
3
Hint
样例解释:
左下方,左上方,右边三块
先找到一个有水的第一个点,进入DFS,先把它标记为干燥,遍历这个点的8个方西,如果某一方向有水,就朝着这个方向,DFS,再把它标记为干燥,直到整个一片都干燥了,退出最开始的DFS,count++,再找另一个有水的点
import java.util.Scanner;
public class Main1 {
private static void dfs(char[][] a, int i, int j) {
a[i][j]='.';//发现后清除水
//8个方向的套路
for (int k = -1; k <2; k++) {//-1 0 1
for (int l = -1; l <2; l++) {//-1 0 1
if(k==0&&l==0){//原地不动
continue;
}
if(i+k>=0&&i+k<a.length&&j+l>=0&&j+l<a[0].length){//i+k为0-M-1 j+l为0-N-1
if(a[i+k][j+l]=='W')//如果8个方向中有水,朝着有水的方向递归,再标记为无水
dfs(a,i+k,j+l);
}
}
}
}
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int M=sc.nextInt();
int N=sc.nextInt();
char[][] a=new char[M][N];
for (int i = 0; i < M; i++) {
a[i]=sc.next().toCharArray();
}
int count=0;
for (int i = 0; i < M; i++) {//8个方向的套路
for (int j = 0; j < N; j++) {
if(a[i][j]=='W'){//找到第一个水洼
dfs(a,i,j);//执行回来回来,清除了一片区域
count++;
}
}
}
System.out.println(count);
}
}
题目链接
回溯
-
递归调用代表开启一个分支,如果希望这个分支返回后某些数据恢复到分支开启前的状态以便重新开始,就要使用回溯技巧
-
全排列的交换法,数独,部分和,用到了回溯
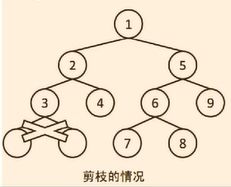
剪枝
-
深搜时,如已明确从当前状态无论如何转移都不会存在(更优)解,就应该中断往下的继续搜索,这种方法称为剪枝
-
数独里面有剪枝
-
部分和里面有剪枝
题9:N皇后问题
在N*N的方格棋盘放置了N个皇后,使得它们不相互攻击(即任意2个皇后不允许处在同一排,同一列,也不允许处在与棋盘边框成45角的斜线上。
你的任务是,对于给定的N,求出有多少种合法的放置方法。
Input
共有若干行,每行一个正整数N≤10,表示棋盘和皇后的数量;如果N=0,表示结束。
Output
共有若干行,每行一个正整数,表示对应输入行的皇后的不同放置数量。
Sample Input
1
8
5
0
Sample Output
1
92
10
import java.util.Arrays;
import java.util.Scanner;
public class N皇后 {
static int count=0;
static int n=0;
static int[] res;
private static void DFS(int row) {//一行一行填写,当前填写row行
if(row==n){
count++;
return;
}
for (int col = 0; col <n; col++) {//判断每一空是否可以
boolean isAc=true;
for (int i = 0; i <row; i++) {//判断当前col是否满足
//res[i]==col此列前面行已出现col
if(res[i]==col||i+res[i]==col+row||i-res[i]==row-col){
isAc=false;
break;
}
}
if(isAc){
res[row]=col;
DFS(row+1);
//res[row]=Integer.MAX_VALUE;
}
}
}
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
while(true){
n=sc.nextInt();
if(n==0){
break;
}
count=0;
res=new int[n];
//Arrays.fill(res,Integer.MAX_VALUE);
DFS(0);
System.out.println(count);
}
}
}
题目链接
题10:素数环
圆环由n个圆组成,如图所示。将自然数1、2,…,n分别放入每个圆,并且两个相邻圆中的数字总和应为质数。
注意:第一个圆的数目应始终为1。
输入值
n(0 输出量 输出格式如下所示。每一行代表环中从顺时针和逆时针1开始的一系列圆圈编号。数字顺序必须满足上述要求。按字典顺序打印解决方案。您将编写一个完成上述过程的程序。在每种情况下都打印空白行。 样本输入 Sample Output 如果一个字符串包含两个相邻的重复子串,则称它为容易的串,其他串称为困难的串, 输入正整数n,L,输出由前L个字符(大写英文字母)组成的,字典序第n小的困难的串。 题目链接 有一类问题,有明确的递推形式,比较容易用迭代形式实现,用递归也有较为明确的层数和宽度 有一类问题,解的空间很大(往往是阶乘级别的),要在所有可能性中找到答案,只能进行试探,尝试往前走一 步,走不通再退回来,这就是dfs+回溯+剪枝 对这类问题的优化,使用剪枝,越早剪越好但这很难6
8
Case 1:
1 4 3 2 5 6
1 6 5 2 3 4
Case 2:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2
import java.util.Scanner;
public class 素数环 {
static int count=1;
private static boolean check(int m){//是质数为true
if(m<2){
return false;
}
for (int i = 2; i*i <=m ; i++) {
if(m%i==0){
return false;
}
}
return true;
}
private static void dfs(int[] res, int k) {
int n = res.length;
if (k == n && check(res[n - 1] + res[0])) {//res已经填完最后一个,要检查头尾和是否为质数
for (int num : res) {
System.out.print(num + " ");
}
System.out.println();
}else{
for (int i = 2; i <= n; i++) {//检查2-n是否是可以
boolean isAc = true;
for (int j = 1; j < k; j++) {//i是否前面已经用过了
if (res[j] == i) {
isAc = false;
break;
}
}
if (isAc && !check(i + res[k - 1])) {//i是否和前面元素和是素数
isAc = false;
}
if (isAc) {//如果i符合要求
res[k] = i;//填入
dfs(res, k + 1);//继续填下一个
res[k] = 0;//回溯
}
}
}
}
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
while (true){
int n=sc.nextInt();
int[] res=new int[n];
res[0]=1;
System.out.println("Case "+count+":");
dfs(res,1);
count++;
System.out.println();
}
}
}
题11:困难的串
如:BB,ABCDACABCAB,ABCDABCD都是容易的,A,AB,ABA,D,DC,ABDAB,CBABCBA都是困难的。
例如,当L=3时,前7个困难的串分别为:
A,AB,ABA,ABAC,ABACA,ABACAB,ABACABA
n指定为4的话,输出ABACpublic class Dfs_6_困难的串 {
public static void main(String[] args) {
int n = 10;
int l = 4;
dfs(l, n, "");
// isHard("0123020120",1);
}
static int count;
private static void dfs(int l, int n, String prefix) {//前l个字母,第n个
//尝试在prefix后追加一个字符
for (char i = 'A'; i < 'A' + l; i++) {
if (isHard(prefix, i)) {//是困难的串,就组合起来输出
String x = prefix + i;
System.out.println(x);
count++;//计数
if (count == n)
System.exit(0);
dfs(l, n, x);
}
}
}
//ABACA i 第一次A i 第二次AC Ai 第三次 ABA CAi
private static boolean isHard(String prefix, char i) {
int count = 0;//截取的宽度
for (int j = prefix.length() - 1; j >= 0; j -= 2) {
final String s1 = prefix.substring(j, j + count + 1);
final String s2 = prefix.substring(j + count + 1) + i;
if (s1.equals(s2))
return false;
count++;
}
return true;
}
}
小结