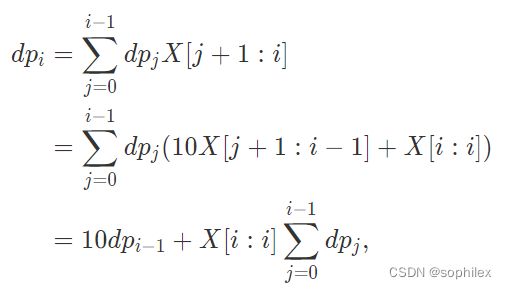AtCoder Beginner Contest 288 题解
D
大意:
给定一个数组A和k,定义一个数组是好的,当且仅当可经过若干次以下操作,使得数组全变成 0。
- 选定一个长度为k区间,令区间里的数都加上x, x是自己选的
有 q个询问,每个询问包括 l,r,问A[l:r]是否是好的
思路:
先考虑暴力,为了让每一个数字都能回到0,我们有一个显然的操作:从左到右遍历,贪心地将对应的数字取0,并向后叠加操作的影响。如果最后能做到大家都是0,就是可以的,否则就不行。这样的复杂度有问题,考虑优化。
不妨先对数组进行一下差分处理,那么每次操作其实就相当于对两个距离为k的点进行对应的加减操作。不难发现,这都是以k为间隔的,换句话说,两个点对k取模之后的值相同。那么我们回到原数组,如果设sum[i]表示区间内所有下标(从0开始)j%k=i的元素的和,那么每次操作之后,每一个sum[i]都会加上相同的值(因为区间加的范围是k,模数不会重合).
显然,这里有一个结论:如果存在i和j,sum[i]!=sum[j],那么最后一定不会做到所有元素为0.这里我们得到了一个必要条件:所有sum[i]的值必须相同,不妨再来证一下它的充分性。
按照一开始讲的思路,从i=l~r-k+1,以i为左端点执行一次使其值为0的操作,那么这样之后除了最后k个元素,其余元素都为0,考虑到条件为所有sum[i]都相等,一番操作之后最后k的元素也必然相等,再执行一次操作就可以了。充分性也得证。
这样的话,我们只要做一下对应的前缀和就可以了
code
#include
using namespace std;
#define ll long long
#define endl '\n'
const ll N=2e5+10;
ll n,m,q;
ll mas[N];
ll sum[N][15];
void solve()
{
cin>>n>>m;
for(int i=1;i<=n;++i)
{
cin>>mas[i];
}
for(int i=1;i<=n;++i)
{
for(int j=0;j>q;
while(q--)
{
ll l,r;
cin>>l>>r;
ll det=sum[r][0]-sum[l-1][0];
bool fl=1;
for(int i=1;i E
大意:
给定n个商品的价格ai 。你要买m个物品,分别是xi。同时给定一个数组c。购买规则为:
购买序号为ii的商品,其标号是未买商品的第j小,其购入价格为 ai+cj
可以买不需要的物品。
问购买所需物品的最小花费。
思路:
无脑做的话,我们需要考虑如下因素:选哪些物品,以及它们的选择顺序
所以显然选dp
对于一个遍历到的物品,我们的选择是买或者不买,以及要买的话,什么时候买。
影响它是当前商品第几小的因素是:前面有几个id比它小的商品,换句话说,在前i-1个商品里,卖出了几个,假设卖出了j个,当前就是第i-j+1小。反而,i后面的商品是什么时候买的,对i的价格并没有影响
所以我们设状态为dp[i][j]表示前i个商品里卖出了j个,考虑到第i个商品的卖出顺序的话:如果它是前i个里第一个卖出了,它是第i小,如果是前面j个都卖完之后再买i,它就是第i-j+1小,这就是它的排名的范围,所以:
dp[i][j]=min(dp[i][j],dp[i-1][j-1]+a[i]+query(id,i));
如果该商品没有强制要求选择的话,还可以从另一个状态转移
[i]) dp[i][j]=min(dp[i][j],dp[i-1][j]);
query()表示c数组的区间最小值,用st表维护即可
code
#include
using namespace std;
#define ll long long
#define endl '\n'
const ll N=5e3+10;
ll n,m,q;
ll l,r;
ll a[N],c[N],x[N];
ll dp[N][N];
bool vis[N];
ll st[N][20];
ll lg[N];
ll query(ll l,ll r)
{
ll len=log(r-l+1)/log(2);
return min(st[l][len],st[r+1-(1<<(len))][len]);
}
void init()
{
for(int i=1;i<=n;++i)
{
st[i][0]=c[i];
}
for(int i=1;i<=log(n)/log(2);++i)
{
for(int j=1;j+(1<>n>>m;
for(int i=1;i<=n;++i) cin>>a[i];
for(int i=1;i<=n;++i) cin>>c[i];
ll ma=0;
for(int i=1;i<=m;++i)
{
cin>>q;
ma=max(ma,q);
vis[q]=1;
}
init();
memset(dp,0x3f,sizeof dp);
dp[0][0]=0;
for(int i=0;i F
大意:
给定一个n位数s。 其有n−1个切割点,一种切割方案包括若干个切割点,其代价是,切割后的所有数字的乘积。
问所有的2^(n−1) 种切割 方案的代价和。
思路:
显然dp
不考虑时间复杂度的话,转移式也很好想:
设dp[i]表示前i位的切割答案,
转移的复杂度是O(n),总时间复杂度就有n^2,考虑优化:
(直接粘官方题解的,懒...
从第二步转移到第三步的时候,我们发现,当j=i-1时,j+1>i-1,X[j+1:i-1]是非法的,所以我们直接略去这种情况,那么此时第二步展开的前半部分就等于10*dp[i-1]了,那么我们就可以O(1)转移了。
code
#include
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
const ll mod=998244353;
ll n,m,q;
string s;
ll ans;
void solve()
{
cin>>n;
cin>>s;
ll sum=1;
for(int i=0;i