数据结构与算法之Python实现——队列
在上一期博客中我们学习了栈这种结构,本期博客将学习一下跟栈很类似的一种结构——队列。
本期知识点:
- 顺序队列
- 循环队列
- 链式队列
- 队列的应用
顺序队列
⚪️什么是队列?
队列是一种跟栈很相似的结构。我们知道栈是一种先进后出的结构,那么队列就像一个排队的队伍一样,排在前面的买到东西后就离开,然后下一个继续买,而后来的人只能按照规矩排到他们的后面,也就是说队列是一种先进先出的结构。
⚪️ 什么是顺序队列?
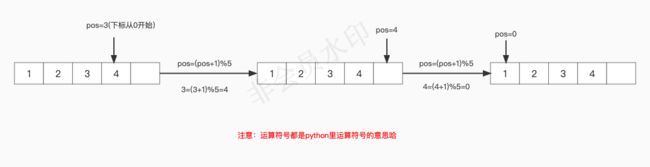
在顺序栈中,我们用到了两个指针“base”和“top”来表示栈底和栈顶元素的下一个位置,在队列中呢我们也用两个指针“front”和“rear”来分别表示队头元素和队尾元素的下一个位置。看下图理解:
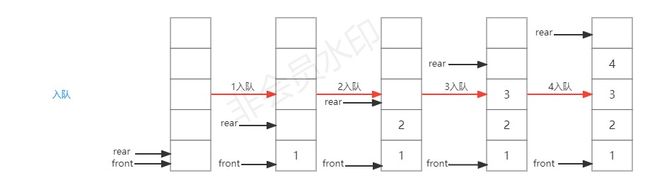
从上图可以看到顺序队列的特性:
- 队空开始入队时队头队尾指针指向同一处
- 入队时是队尾指针在移动,类似于顺序栈的top指针
- 出队时是队头指针在移动
- 在出队中,若队头队尾指针相遇了,则表明队空了
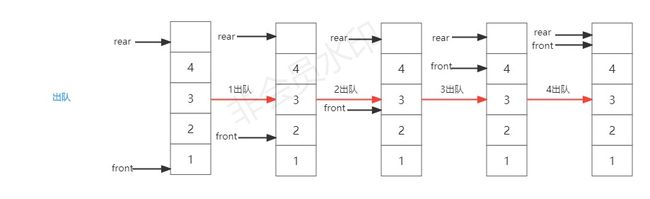
同时,它也有一个很明显的缺点:在出队的操作中,当4出队后,队尾队头指针都已经指向了这个顺序队列的末端,这时如果我们再进行入队的话肯定会发生队尾指针的溢出。
但实际上,这个队列此时明显是空的。所以,如果我们照着前面那样来设计顺序队列的结构的话肯定会造成很大的存储空间的浪费。对于这个缺点,我们可以在每次出队后,将队列中的元素往前移一位,也就是出队是保持队头指针不动,队尾指针再次移动。
但这样设计的话操作又太过于繁琐,于是,为了弥补顺序队列的不足,我们引入循环队列。
循环队列
思想实现
首先,我们需要明确设计循环队列的目的:为了解决顺序队列元素完全出队后,队头队尾指针指向队列的末尾而无法再入队的问题。
那么下面以循环队列接着处理上面遗留的问题,假如经出队后,此时队头队尾指针指向了队列的末尾。
因为是个循环队列,所以我们此时再入队,队尾指针应该继续移动,然而队尾后面已经没有存储空间了,所以它应该指向有空间的地方。那么我们就可以使它指向队列的“头部”(这里头部是相对的头部,本质上来说是没有头部的,因为它是一个循环队列)。
此时,原本的队头指针在尾部,原本的队尾指针现在出现在了头部。那么这种情况是不是又回到了一个空的顺序队列呢?
我们要实现的就是使尾部的指针加1后能够跳到头部去。实现代码如下:
rear = (rear + 1) % length # length是队列的长度
初始化
这里我们创建一个关于队列的类,所有的操作都通过这个类实例化出的对象调用相关的函数实现。首先是初始化:
class Queue:
def __init__(self,length):
self.length = length # 队列的长度
self.elem = [None] * self.length # 队列存放的元素
self.rear = 0 # 队尾指针
self.front = 0 # 对头指针
在进行其他的操作之前我们要考虑这样一个问题,在上面所描述的循环队列中,初始的空队列,队头队尾指针是相等的,当持续入队直至队满时,队头队尾指针又是相等的。那么此时这个队列到底是空的还是满的呢?为了后续的操作,我们需要先解决这个问题。
一个初始化的队列队头队尾指针相等是母庸置疑的,于是我们就以队头队尾指针相等时表示队空。那么如何来表示队满呢?我们可以在队列的尾部多设一个空间,当将元素入队至队满,队尾指针就会指向这个另设的空间,当队满时队尾指针再加1就到了队列头部与队头指针相等,此时就可以以这个条件表示队满。
如下图(红色格子表示额外使用的空间):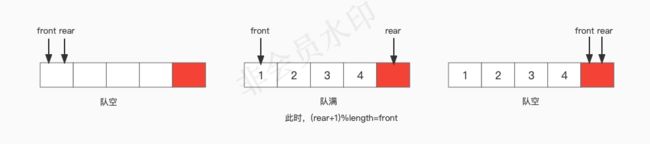
这个问题解决后,我们就继续实现队列的相关操作。
求队列长度
注意:在循环队列中队列的长度不能用队尾指针与队头指针的差值来表示,因为是一个循环队列,队尾指针可能会出现在队头指针的“前面”(相对而言)。
# 获取队列长度
def get_length(self):
count = 0 # 计数器,统计队列中元素的个数
m = self.front # 为了不影响原本的指针,这里用m,n两个变量来代替它们进行遍历
n = self.rear
while m != n: # 当队头队尾指针不相等时作为循环执行的条件
count += 1 # 计数
m = (m + 1) % self.length # 队头指针向队尾指针移动
return count
入队
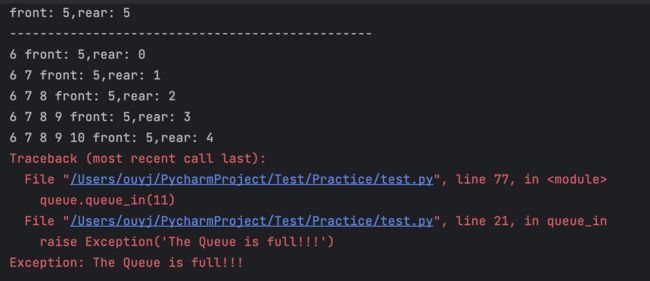
入队前需要考虑队列是否已满,满了就不能入队了。判断条件也就是我们在前面说的那样,当队尾指针在循环意义上加1等于队头指针时,就表示队列已满。
若队列未满,则将元素入队,而后队尾指针加1
# 入队
def queue_in(self,data):
if (self.rear + 1) % self.length == self.front: # 入队时需考虑队列是否已满
print('The queue if full!')
return
self.elem[self.rear] = data # 元素入队
self.rear = (self.rear + 1) % self.length # 队尾指针移动
出队
与入队相反,出队则需要判断队列是否为空。我们在前面也说到过,当队头队尾指针相同时就表示队空。此时我们将队头指针向后移动一位即可。因为出队是将队头元素取出,而队头指针始终是指向队头的,出队就是要让队头的后一个元素成为队头就行了。
# 出队
def queue_out(self):
if self.rear == self.front: # 判断队列是否为空
raise Exception('The Queue is empty!!!')
self.front = (self.front + 1) % self.length # 出队就是往后移动队头指针
打印队列中的元素
在打印队列中的元素的时候,一定是m也就是队头指针在移动,而队尾指针所在处一定是空的,所以当队头队尾指针相同时,就表示队列中的元素已打印完成。
# 打印队列中的元素
def queue_print(self):
m = self.front # 用m来代替队头指针移动
n = self.rear # 用n来代替队尾指针移动
while m != n: # 循环执行的条件
print(self.elem[m],end=" ") # 继续打印队头元素
m = (m + 1) % self.length # 队头指针向后移动
验证循环队列的操作
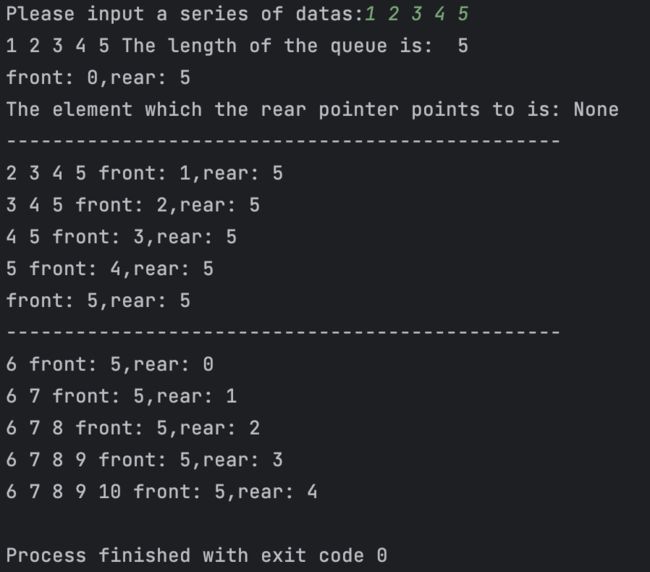
# 输入数据,这里以整型数字作为例子
a = list(map(int,input('Please input a series of datas:').split(" ")))
# 实例化Queue对象,为了方便表示队空队满,我们另设一个额外的空间
queue = Queue(len(a) + 1)
# 入队
for i in range(len(a)):
queue.queue_in(a[i])
# 打印此时队列中的元素
queue.queue_print()
# 此时队列的长度
print('The length of the queue is: ',queue.get_length())
# 此时队头队尾指针的值
print('front: %d,rear: %d' % (queue.front,queue.rear))
# 打印此时队尾指针指向的元素
print('The element which the rear pointer points to is:',queue.elem[queue.rear])
print('------------------------------------------------')
# 依次将队列中的元素出队,每出队一个元素就打印队列中的元素和队头队尾指针的值
for i in range(queue.get_length()):
# 出队一个元素
queue.queue_out()
# 打印出队一个元素后队列中剩余的元素
queue.queue_print()
print('front: %d,rear: %d' % (queue.front,queue.rear))
print('------------------------------------------------')
# 继续入队,因为我们已经设置好循环队列的大小了,所以这里就仍然用5个元素进行入队
b = [6,7,8,9,10]
for i in range(len(b)):
queue.queue_in(b[i])
queue.queue_print()
print('front: %d,rear: %d' % (queue.front,queue.rear))
queue.queue_in(11)
链式队列
链队同链栈是一个道理,相当于是将顺序队列的中的每个元素分割成一个一个的个体,再用某种方式将这些个体连接起来,而指针仍然是独立于链队之外。
初始化
因为说到指针是独立于链队之外的,所以我们为节点单独设一个类。在这里我们初始化链队需要将队头队尾指针指向一个空节点,这个空节点并无任何用处,仅仅只是为了初始化及后续操作而已。
同样,大家也可以考虑一个问题:可不可以直接将两个指针置为“None”呢?(这样设置不方便后续的入队出队操作)。
下面话也不多说,直接看。
# 节点
class QNode:
def __init__(self,data):
self.elem = data
self.next = None
# 链队
class Queue:
def __init__(self):
# 队头队尾指针初始化指向空节点
self.front = self.rear = QNode(None)
入队
入队的操作其实很简单,也是移动队尾指针即可,但是不需要考虑队列是否满的问题,因为是队列是通过生成节点动态增加的。
# 入队
# 入队是队尾指针移动,队尾指针始终指向链队中的最后一个元素
def Queue_in(self,data):
# 生成一个新节点
node = QNode(data)
# 队尾指针所在节点指向新生成的节点
self.rear.next = node
# 队尾指针指向新生成的节点
self.rear = node
出队
出队操作就比较复杂。在出队时我们还是需要判断队列是否为空,这里还是队头队尾指针相同时就表示队空。
同时还要考虑一个问题,当链队中剩余最后一个元素时,若要继续出队,按照上面队空的概念,此时应该是队头队尾指针相同,同时指向最后一个元素,但是按照更上面的说法,队尾指针始终指向的是链队中的最后一个元素,这样就矛盾了。
那么我们该如何去处理呢?这时只需要单独地操作一下即可:当要将最后一个元素出队时,我们直接将那个节点变成空节点即可,这里又回到了链队初始化的时候了。
# 出队
# 出队是队头指针进行移动,队头指针始终指向第一个节点(空节点)
# 队头指针移动到下一个节点,相对而言下一个节点也就成了“空节点”
def Queue_out(self):
# 判断链队是否为空,若队头队尾指针相同就表示链队是空的
if self.front == self.rear:
raise Exception('The Queue is empty!!!')
# 若将要出队的元素是最后一个元素,那么此时直接将队尾指针所指节点变成空节点即可
if self.rear.next == None:
self.rear = QNode(None)
# 用cur表示队头指针指向节点的上一个节点,后面需要将其释放掉
cur = self.front
self.front = self.front.next
# 释放cur所占用的内存
del cur
获取链队的长度
def get_length(self):
# 用cur来代替指针进行遍历,此时cur指向队列中第一个元素(第一个元素也可以为空)
cur = self.front.next
# 计数器
count = 0
while cur is not None:
count += 1
cur = cur.next
return count
打印链队中的元素
# 打印队列中的元素
def Queue_print(self):
cur = self.front.next
while cur is not None:
print(cur.elem,end=" ")
cur = cur.next
验证链队的操作
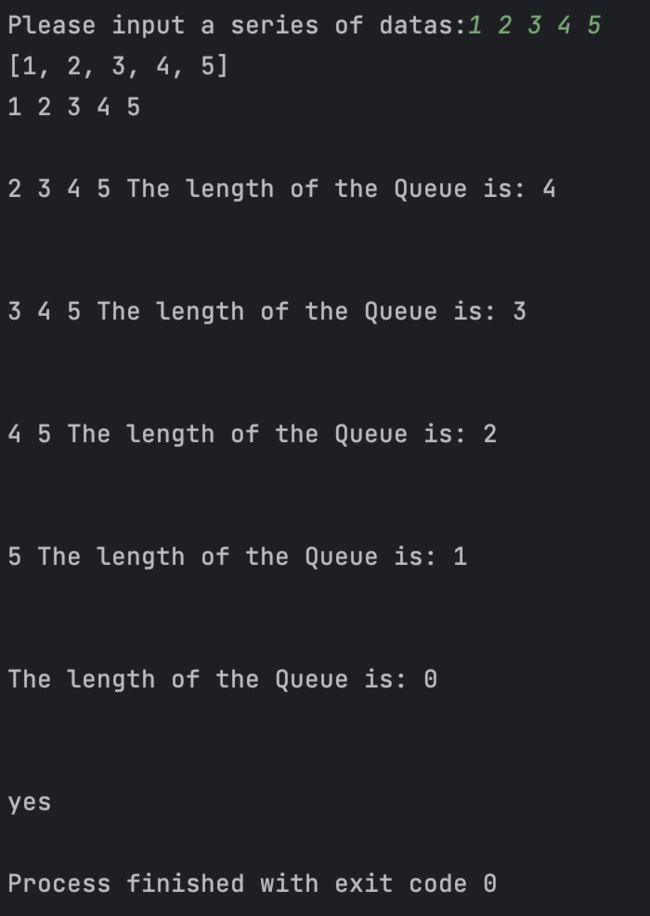
a = list(map(int,input('Please input a series of datas:').split(" ")))
print(a)
# 实例化Queue对象
queue = Queue()
# 入队
for i in range(len(a)):
queue.Queue_in(a[i])
# 打印此时队列中的元素
queue.Queue_print()
print("\n")
# 依次出队,每出队一个元素就打印依次队列中的元素
while queue.front.next != None:
queue.front = queue.front.next
queue.Queue_print()
print('The length of the Queue is:',queue.get_length())
print("\n")
if queue.front.next == None and queue.rear.next == None:
print('yes')
总结
队列是一种先进先出的数据结构。有顺序队列、循环队列、链队三种形式。
顺序队列结构简单,但是存储空间有限,且不利于对存储空间的利用,入队后出队都需要重新移动指针。
循环队列其实也是顺序队列,不过就是增强了对存储空间的利用,入队后出队不用重新移动指针。
链式队列就是不用人为分配空间,是自动增长的。读者们可以考虑考虑循环的链式队列如何实现?
这期博客就到这里啦~下次再见