最长公共子序列问题 C++ (超详细)
最长公共子序列问题
问题描述
若给定序列X={x1,x2,…,xm},则另一序列Z={z1,z2,…,zk},是X的子序列是指存在一个严格递增下标序列{i1,i2,…,ik}使得对于所有j=1,2,…,k有:zj=xi。
例如,序列Z={B,C,D,B}是序列X={A,B,C,B,D,A,B}的子序列,相应的递增下标序列为{2,3,5,7}。
给定2个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列。
给定2个序列X={x1,x2,…,xm}和Y={y1,y2,…,yn},找出X和Y的最长公共子序列。
解题思路
算法描述:
由最长公共子序列问题的最优子结构性质建立子问题最优值的递归关系。用c[i][j]记录序列和的最长公共子序列的长度。其中, Xi={x1,x2,…,xi};Yj={y1,y2,…,yj}。当i=0或j=0时,空序列是Xi和Yj的最长公共子序列。故此时C[i][j]=0。其它情况下,由最优子结构性质可建立递归关系如下
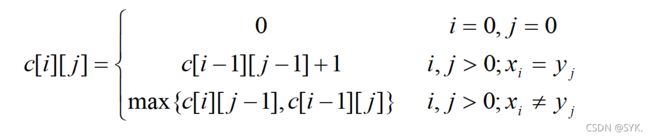
操作起来就是按两个字符串的长度分别为长+1和宽+1,构造一个二维数组用来存放结果,初始时要将此方阵的最上面的行和最左面的列全部填0;
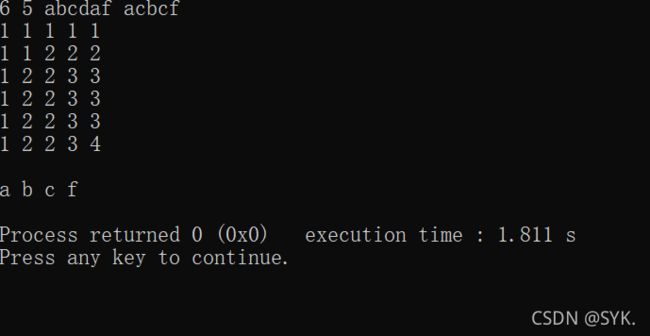
以串分别为 acbcf 和 abcdaf 为例
这是初始化

然后从左上角开始将行跟列进行比较如果相同那么此格的值赋值为左上角的值+1,如果不相同那么将此格左边和上边的值进行比较哪个大 此格值便赋值为哪个
由此我们得到结果如下

此方阵的右下角即为最长公共子序列的长度
求最长公共子序列的具体内容
由方阵的形成过程可知右下角是由之前的一次次赋值从而最终得来的,想要依次找到具体内容只需要找到右下角是谁赋的值然后依序倒退就可以了 由此我们可以得到一条形成右下角依次赋值来源的路线
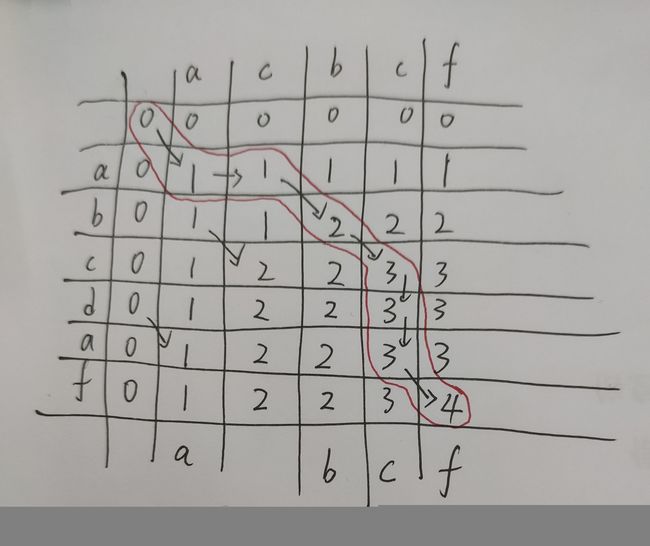
在倒退过程中我们要找到的就是这条路线上行与列相同的,即此格子中的值是由其左上角+1得来的
由此我们可以得到

结果为 abcf 即我们所求的 acbcf 和 abcdaf 的最长公共子序列
结果有两个最长公共子序列
只有一个最长公共子序列的结果自然不用说了,但当结果有两个呢
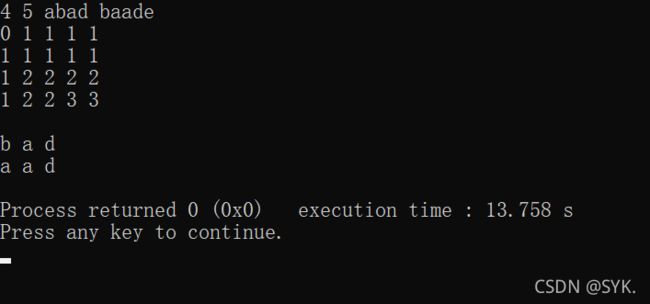
以 abad 和 baade 为例
当进行到最后一步找路线时问题出现了
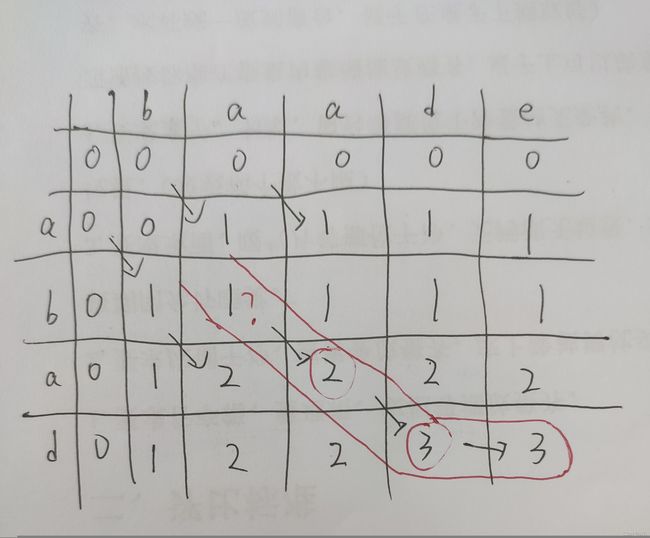
它的左边和上面的值相等 此时我们无法确定这条路线应该向上还是向左
造成这种情况的原因是我们取左边和上面的值大的一个 并没有说明相等时怎么办 于是这种情况会产生两个结果 我们分别按左和上 将路线画出来
由此我们得到结果分比为 bad 和 aad 造成这种现象的原因就是当上面和左面的值相等时取的边不同导致的
但两个都是正确答案
代码如下
#include
#include
using namespace std;
int re[200][200];//记录路径数组1
int re1[200][200];//记录路径数组2
char s1[200],s2[200];//记录最长子序列数组1、2
int i1=0,i2=0;
void p(char t[],int n,int m){//根据记录路径数组1求最长子序列
if(m==0 || n==0) return;
if(re[n][m]==0)//判断来源是否为左上角
{
p(t,n-1,m-1);//传参为左上角进行递归
s1[i1]=t[n-1];
i1++;
}
if(re[n][m]==1)//判断来源是否为上边
p(t,n-1,m);//传参为上面一格进行递归
if(re[n][m]==2)//判断来源是否为左边
p(t,n,m-1);//传参为左边一格进行递归
}
void p1(char t[],int n,int m){//根据记录路径数组2求最长子序列 与p相同
if(m==0 || n==0) return;
if(re1[n][m]==0)
{
p1(t,n-1,m-1);
s2[i2]=t[n-1];
i2++;
}
if(re1[n][m]==1)
p1(t,n-1,m);
if(re1[n][m]==2)
p1(t,n,m-1);
}
int main()
{
int n,m,i,j,l=0,k;
cin>>n>>m;
//分别输入字符串长度 (这里只是作业要求
//实际上可以直接输入字符串然后用函数求长度)
getchar();
char a[n],b[m];
int z[n+1][m+1];//记录赋值数组
//初始化赋值
for(i=0;iz[i][j-1])//上面的值大于左面的
{
z[i][j]=z[i-1][j];//赋值为上面的值
re[i][j]=1;//设1代表来源为上面
}
else //此时为左面的值大于等于上面的
{z[i][j]=z[i][j-1];//赋值为左面的值
re[i][j]=2;//设2代表来源为左面
}
}
//下面这次遍历路径存储在re1数组里
//与上面的区别是当上面和左面相等时取上面的值
for(int i=1;i=z[i][j-1])//这里的判定条件不同
{
re1[i][j]=1;//上面
}
else {
re1[i][j]=2;//左面
}
}
//输出赋值数组
for(i=1;i