C语言穷举法最长公共子序列,最长公共子序列问题

Biological applications often need to compare the DNA of two (or more) different organisms. A strand of DNA consists of a string of molecules called bases, where the possible bases are adenine, guanine, cytosine, and thymine. Representing each of these bases by its initial letter, we can express a strand of DNA as a string over the finite set {A,C,G,T}.

这是生物学应用中最为常见的“最长公共子序列问题”。

动态规划原理

能够用动态规划解决的问题，通常具有两种属性：第一，存在最优子结构，即可以用“剪切，粘帖”的方法来证明；第二，具有重叠子问题。

递归和穷举算法分析

在矩阵链乘法的问题中，可以使用递归和穷举两种方法来解决最优的括号化方案。其中，对每一种方案计算乘法运算次数。

用穷举法的时候，表中的每一个节点都必须访问，记访问一个节点的时间为$b_k$

则有递推式：

$b_n= sum_{k=0}^{n-1}b_kb_{n-1-k}$

该递推式符合卡特兰数，可以推出通项公式为：

$b(n)=frac{4^n}{sqrt{pi}n^{3/2}}(1+O(1/n))$

阶是关于n的指数函数。

用Recursive-Matrix-Chain递归求解，递推式符合

$T(n)geq1+sum_{k=1}^{n-1}(T(k)+T(n-k)+1) qquad n>1$

可以求得递推公式为：

$T(n)geq2^{n-1}$

可见朴素递归算法比穷举好一些。

动态规划问题和分治法区别

在merge-sort过程中，可以发现，问题不具有重叠字问题的性质，如下图所示，所有的子问题均不重叠。

最大化矩阵括号方案

最大化矩阵括号化方案，问题仍然具有最优子结构性质。因为“剪切，粘帖”的处理方式没有变。

假设最大括号化方案能够使结果最优，则其中的划分为：

$A_1A_2dots dots A_kA_{k+1}dots A_j$

如果该方案不是最优的，总可以找到另外一种方案如下：

$A_1A_2dots A_iA_{i+1}dots dots A_j$

来替代该方案，使得结果最优。

贪心和动态规划的区别

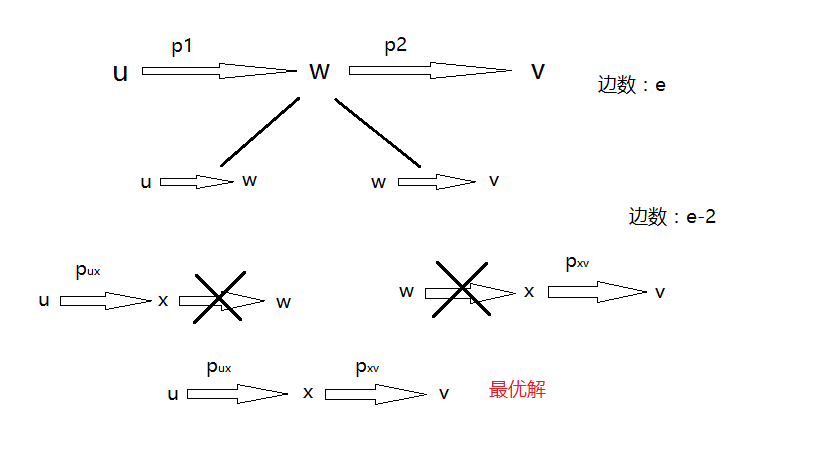
贪心算法的原理是：我们不必计算原问题的最优解，总是可以在求解子问题的时候划分出$A_iA_{i+1}dots A_j$，选定的k使得$p_{i-1}p_{k}p_{j}$最小。这样的贪心算法并不能够得到最优解。原因如下：

虽然我们求出来的最优解如红色的图，但很有可能

$p_{u-1}p_wp_v

原因如下：最优解的函数表达式与贪心中的$p_k$函数表达式不同，所以贪心算法并不能够用于最优解问题。

编程验证：

贪心策略如下：

//下面这是用错误的贪心算法求解的问题：

Matrix_Chain Matrix_Chain_Order_greedy(int p[])

{

int N=n-1;

Matrix_Chain T_greedy;

for(int i=0;i

T_greedy.m[i][i]=0;

for(int l=2;l<=N;l++)

{

for(int i=1;i<=N-l+1;i++)

{

int j=i+l-1;

T_greedy.m[i-1][j-1]=INFINITY;

int q_min=INFINITY;

for(int k=i;k<=j-1;k++)

{

int q=T_greedy.m[i-1][k-1]+T_greedy.m[k][j-1]+p[i-1]*p[k]*p[j];

if(q_min>p[i-1]*p[k]*p[j])

{

q_min=p[i-1]*p[k]*p[j];

T_greedy.m[i-1][j-1]=q;

T_greedy.s[i-1][j-1]=k-1;

}

}

}

}

return T_greedy;

}

结果如图：

很显然地看出，greedy_result得到了不同的括号化结果。

钢条切割问题的限制

如果我们限制，在r=4的时候，只能够切割成两段长度为1的钢条，则r=4的时候，最优切割方案1+1+1+1无法成立。

外币兑换问题

该问题可以看成是一种矩阵链乘法的变形，当佣金$C_k$为任意值的时候，并不符合最优子结构的性质。

具体的描述见下图：

合并问题的代价，可以描述为$C_k$

解决每个问题所需要的代价为$R_k$

总代价的递推式为：

$R_k+C_k$

$R_{k2}+C_{k_2}$

如果$C_k$不为常数，假设它可以用一个$f(k)$描述，则问题的代价可以描述为：

$R_k+f(k)$

动态规划算法只能保证$R_k$的最优解，并不能保证$f(k)$的最优解。

最长公共子序列

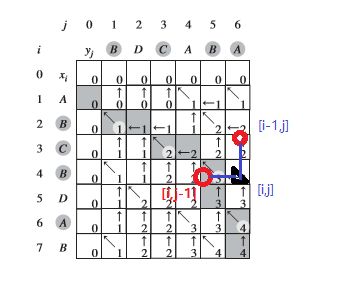
最长公共子序列的求解，如下图所示：

可以看到，最长公共子序列的依赖关系如上图所示，[i,j]的值取决于{[i-1,j-1],[i,j-1],[i-1,j]}

实现方法如下：

LCS_len.h

#include

#include

#include

#define M 6

#define N 7

wchar_t b[N+1][M+1]={'S'}; //表示起点start

int c[N+1][M+1]={0};

wchar_t northwest=L'\\', up=L'|', leftway=L'-';

void LCS_length(char *x,char *y)

{

for(int i1=0;i1<=N;i1++)

b[i1][0]='S';

for(int j1=0;j1<=M;j1++)

b[0][j1]='S';

for(int i=1;i<=N;i++)

{

for(int j=1;j<=M;j++)

{

if(x[i]==y[j])

{

c[i][j]=c[i-1][j-1]+1;

b[i][j]=northwest; //Northwest往左上

}

else

{

if(c[i-1][j]>=c[i][j-1])

//c[i-1][j-1] 过渡到 c[i][j]，需要将c[i-1][j]和c[i][j-1]比较大小

//取较大的那一个值

{

c[i][j]=c[i-1][j];

b[i][j]=up; //Up往上