按照前序遍历创建二叉树及树的四种遍历方式

一.二叉树的介绍

        二叉树的特点是二叉树的每个结点的度都不大于2，可以视为每个结点都有左孩子和右孩子。故二叉树结点的数据结构为

 

二.二叉树的特点

    1.设根结点所在的层数为第1层，则第i层最多有个结点。

    2.深度为k的二叉树最多有个结点。

    3.对任何一个二叉树，设其中度为0的结点个数为n0,度为1的结点个数为n1,度为2的结点个数为n2,则n0=n2+1。

    4.对具有n个结点的完全二叉树来说，如果从上到下从左向右的顺序对所有的结点进行编号，则对于编号为i的结点有：

        a)若i>0,则结点的双亲结点编号为；若i=0，则该结点为根结点，没有双亲结点。

        b)若,则它的左孩子结点编号为;否则无左孩子。

        c)若,则它的右孩子结点编号为;否则无右孩子。

        d)深度为k = [log(n+1)],结果为小数时进行向上取整。

三.创建二叉树

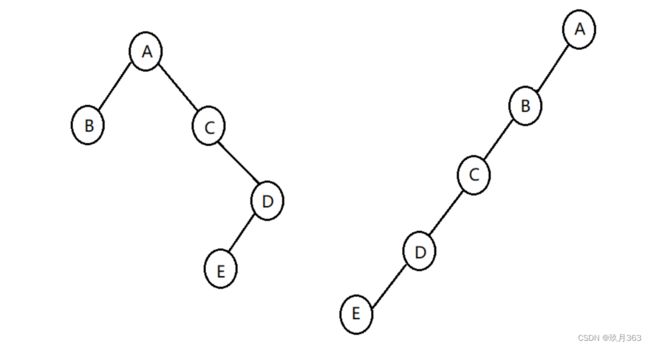
        仅用前序遍历并不能确定一棵二叉树的全部形态，比如仅用ABCDE表示的二叉树的形态就有以下两种:

         所以为了确保我们的前序遍历对应的树是唯一的,我们需要将原本的树构造成一颗比较完整二叉树(即节点存在空节点我们也要表示),为此我们要将树中缺少的节点进行补齐,即用一种特别的字符来表示我们的空节点(想用什么字符看个人喜好),这里我们采用#来代表空节点,所以对于左边的树结构我们将其补全后的前序遍历结果将变成:AB##C#DE###;

        创建二叉树的思路:创建二叉树一般使用递归思路创建,即先创建根节点,然后创建根节点的左子树,接着创建根节点的右子树,一般来说,树的创建是先采用数组来存储需要添加的数据域的数据,但是我们为了操作的简便性便直接读取字符来实现;

注:由于在实例中是用的字符,所以elemtype类型定义为char,对于数字的话可以直接该char为int就能解决对应问题(注:字符改数字空节点代表符也要进行相应改变,比如改为0)

 四.遍历二叉树

        二叉树的遍历一般有四种,即前序遍历,中序遍历,后序遍历,以及层次遍历,前三者的区别就在于当前节点在何时输出,先输出就是前序,中间输出就是中序,最后输出便是后序了,层次遍历的话便是从上到下,从左到右对树进行遍历;

        遍历又分为递归遍历与非递归遍历,这里我们只说明递归遍历(os:非递归真的太绕啦!),对于前中后序遍历没有太多理解点,我们直接看代码操作就好,(注:我这是方便理解才进行这种书写方式,其实其中可以进行简写,如只判断当前节点是否为空然后来控制是否输出当前节点数据)

 

 我们抓重点讲一下层次遍历,说到层次遍历的特点,从上到下,从左到右,我们首先想到的就是树的节点排序也是从上到下从左到右,那么我们是不是可以从中借鉴一二呢,答案是肯定的,对于树的节点排序我们是采用人工的观察排序,那如何将操作机械化呢,我采用的是队列的方式,因为队列是先进先出,

 根据代码,如果根节点不为空,我们就让根节点入队列,然后从队列中弹出根节点,让根节点的左右节点进入队列,然后进入完之后在弹出一个新节点,让新节点的左右节点进入队列,这样操作就可以达到层次遍历的要求了

五.完整代码

#include
#include
typedef char elemtype;//对char类型进行重定义,即elemtype就代表char类型
typedef struct Node//定义节点结构体
{
    elemtype elem;///定义数据域
    struct Node* leftNode;//定义左子节点
    struct Node* rightNode; //定义右子节点
}Node;

//队列的定义
#define maxsize 100
#define _CRT_SECURE_NO_WARNINGS
typedef struct
{
    Node* elem[maxsize];
    int front, rear;
}seqqueue;

//初始化队列
seqqueue* initqueue()
{
    seqqueue* queue = (seqqueue*)malloc(sizeof(seqqueue));
    queue->front = queue->rear = 0;
    return queue;
}

//判断队满
int isfull(seqqueue* queue)
{
    if ((queue->rear + 1) % maxsize == queue->front)
    {
        return 1;
    }
    else
    {
        return 0;
    }
}

//判断队空
int isempty(seqqueue* queue)
{
    if (queue->rear == queue->front)
    {
        return 1;
    }
    else
    {
        return 0;
    }
}

//入队方法
void inqueue(seqqueue * queue, Node* node)
{
    if (isfull(queue))
    {
        printf("queue is full can not inqueue");
    }
    else
    {
        queue->elem[queue->rear] = node;
        queue->rear = (queue->rear + 1) % maxsize;
    }
}

//出队方法
Node* enqueue(seqqueue* queue)
{

    if (isempty(queue))
    {
        printf("queue is empty can not enqueue");
        return NULL;
    }
    else
    {
        Node* node;
        node = queue->elem[queue->front];
        queue->front = (queue->front + 1) % maxsize;
        return node;
    }
}

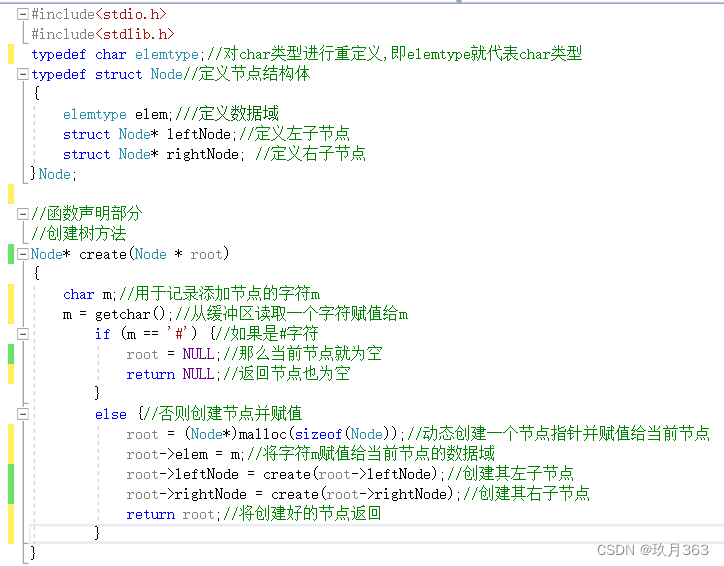
//函数声明部分
//创建树方法
Node* create(Node * root)
{
    char m;//用于记录添加节点的字符m
    m = getchar();//从缓冲区读取一个字符赋值给m
        if (m == '#') {//如果是#字符
            root = NULL;//那么当前节点就为空
            return NULL;//返回节点也为空
        }
        else {//否则创建节点并赋值
            root = (Node*)malloc(sizeof(Node));//动态创建一个节点指针并赋值给当前节点
            root->elem = m;//将字符m赋值给当前节点的数据域
            root->leftNode = create(root->leftNode);//创建其左子节点
            root->rightNode = create(root->rightNode);//创建其右子节点
            return root;//将创建好的节点返回
        }
}

//前序遍历
void preorder(Node* root)
{
    //先打印当前节点数据
    printf("%c ", root->elem);
    //在向左子树递归前序遍历
    if (root->leftNode != NULL) {//如果左子树不为空
        preorder(root->leftNode);
    }
    //最后向右子树递归前序遍历
    if (root->rightNode != NULL) {
        preorder(root->rightNode);
    }
}

//中序遍历
void infixorder(Node* root)
{
    //先向左子树递归前序遍历
    if (root->leftNode != NULL) {//如果左子树不为空
        infixorder(root->leftNode);
    }
    //在打印当前节点数据
    printf("%c ", root->elem);
    //最后向右子树递归前序遍历
    if (root->rightNode != NULL) {
        infixorder(root->rightNode);
    }
}

//后序遍历
void postorder(Node* root)
{
    //先向左子树递归前序遍历
    if (root->leftNode != NULL) {//如果左子树不为空
        postorder(root->leftNode);
    }
    //在向右子树递归前序遍历
    if (root->rightNode != NULL) {//如果右子树不为空
        postorder(root->rightNode);
    }
    //最后打印当前节点数据
    printf("%c ", root->elem);
}

//层次遍历
void level(Node* root)
{
    //先创建好队列
    seqqueue* queue = initqueue();
    //遍历树
    if (root != NULL) {//如果根节点不为空
        inqueue(queue, root);//根节点入队列
    }
    //判断队列状况
    while (!isempty(queue)) {//如果队列不为空
        //从队列中出列一个节点
        Node* temp = enqueue(queue);
        printf("%c ", temp->elem);//先打印该节点数据
        if (temp->leftNode != NULL) {//如果左子节点不为空
            inqueue(queue, temp->leftNode);//左子节点入队列
        }
        if (temp->rightNode != NULL) {//如果右子节点不为空
            inqueue(queue, temp->rightNode);//右子节点入队列
        }
    }
    printf("\n");
}

int main()
{
    Node* root;//定义一个根节点指针
    root = NULL;//将根节点指针赋值为空
    printf("请按前序遍历依次输入节点数据:(#表示空节点)\n");
    root = create(root);//构建树
    int choice = 1;//用于遍历选择的参数
    while (choice) {
        printf("1.前序遍历   2.中序遍历\n");
        printf("3.后序遍历   4.层次遍历\n");
        printf("      0.退出遍历       \n");
        printf("请选择你想要的遍历方式:");
        scanf_s("%d", &choice);
        switch (choice) {
        case 1:
            printf("前序遍历的结果是:\n");
            preorder(root); printf("\n"); break;
        case 2:
            printf("中序遍历的结果是:\n");
            infixorder(root); printf("\n"); break;
        case 3:
            printf("后序遍历的结果是:\n");
            postorder(root); printf("\n"); break;
        case 4:
            printf("层次遍历的结果是:\n");
            level(root); printf("\n"); break;
        default:
            printf("请输入正确数字!"); break;
        }
    }
}

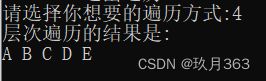
 六.实际案例

这个实操案例我们就用之前举例的ABCDE来测试即(AB##C#DE###)操作