Codeforces Round 783 补题

官网链接

div2

C Make it Increasing

You are given an array a consisting of n positive integers, and an array b, with length n. Initially b_i = 0 for each 1 ≤ i ≤ n.

In one move you can choose an integer i (1 ≤ i ≤ n), and add ai to bi or subtract ai from bi. What is the minimum number of moves needed to make b increasing (that is, every element is strictly greater than every element before it)?

Input
The first line contains a single integer n (2 ≤ n ≤ 5000).

The second line contains n integers, a1, a2, …, an (1 ≤ a_i ≤ 10⁹) — the elements of the array a.

Output
Print a single integer, the minimum number of moves to make b increasing.

Examples
input
5
1 2 3 4 5
output
4

input
7
1 2 1 2 1 2 1
output
10

input
8
1 8 2 7 3 6 4 5
output
16
题解：
因数据范围为5000，所以可以O(N²)出解。
暴力：首先b数组一定有一个不需要增和减，即b数组必有一个0，暴力枚举每个数(假设他不需要变，即0)，以这个0为标准点，令从左和从右该数的绝对值递增，用last变量记录上一次已经修改后的数，即可出解。但要注意答案刚开始要初始化为一个很大的数，如1e18。

#include

using namespace std;

typedef long long ll;
typedef pair<int,int> pii;

#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define lowbit(x)   ((x)&(-x))
#define fi first
#define se second
#define endl '\n'
#define pb push_back

template <typename T> bool chkMax(T &x, T y) { return (y > x) ? x = y, 1 : 0; }
template <typename T> bool chkMin(T &x, T y) { return (y < x) ? x = y, 1 : 0; }

template <typename T> void inline read(T &x) {
    int f = 1; x = 0; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }
    while (c <= '9' && c >= '0') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
    x *= f;
}

const int N = 5010;
ll a[N];

int main()
{
    int n;
    scanf("%d",&n);
    for(int i = 1;i <= n;i++)   scanf("%lld",&a[i]);
    ll ans = 1e18;//需要开的很大
    for(int i = 1;i <= n;i++)
    {
        int x = i;
        ll last = 0;
        ll res = 0;
        for(int j = x - 1;j >= 1;j--)
        {   
            if(j == x - 1)  
            {
                last = a[j];
                res++;
                continue;
            }
            res += last / a[j] + 1;
            last = last / a[j] * a[j] + a[j];
        }
        for(int j = x + 1;j <= n;j++)
        {
            if(j == x + 1)
            {
                last = a[j];
                res++;
                continue;
            }
            res += last / a[j] + 1;
            last = last / a[j] * a[j] + a[j];
        }
        chkMin(ans,res);
    }
    printf("%lld",ans);
    return 0;
}

div1

B Optimal Partition

You are given an array a consisting of n integers. You should divide a into continuous non-empty subarrays (there are 2ⁿ⁻¹ ways to do that).
Let s=a_l + a_l+1 + … + a_r. The value of a subarray a_l,a_l+1,…,a_r is:
(r−l+1) if s>0,
0 if s=0,
−(r−l+1) if s<0.
What is the maximum sum of values you can get with a partition?
Input
The input consists of multiple test cases. The first line contains a single integer t (1 ≤ t ≤ 5⋅10⁵) — the number of test cases. The description of the test cases follows.
The first line of each test case contains a single integer n (1 ≤ n ≤ 5⋅10⁵).

The second line of each test case contains n integers a₁, a₂, …, a_n (−10⁹ ≤ a_i ≤ 10⁹).

It is guaranteed that the sum of n over all test cases does not exceed 5⋅10⁵.
Output
For each test case print a single integer — the maximum sum of values you can get with an optimal parition.
Example
input
5
3
1 2 -3
4
0 -2 3 -4
5
-1 -2 3 -1 -1
6
-1 2 -3 4 -5 6
7
1 -1 -1 1 -1 -1 1
output
1
2
1
6
-1
Note
Test case 1: one optimal partition is [1,2], [−3]. 1+2>0 so the value of [1,2] is 2. −3<0, so the value of [−3] is −1. 2+(−1)=1.

Test case 2: the optimal partition is [0,−2,3], [−4], and the sum of values is 3+(−1)=2.

#include

using namespace std;

typedef long long ll;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define lowbit(x) ((x) & (-x))
#define endl '\n'

const int N = 5e5 + 10,inf = 1e9;
int n,tr[N],a[N];

void add(int x,int v)
{
    for(int i = x;i <= n;i += lowbit(i))//x 不能是0，不然lowbit(0)也是0就死循环了
        tr[i] = max(tr[i],v);
}

int sum(int x)
{
    int res = -inf;
    for(int i = x;i ;i -= lowbit(i))
        res = max(res,tr[i]);
    return res;
}

void solve()
{//DP + 树状数组,有贪心的味道
    cin >> n;
    vector<ll> s(n + 1);//细节n + 1
    for(int i = 1;i <= n;i++)   cin >> a[i],s[i] = s[i - 1] + a[i];

    auto v = s;
    sort(v.begin(),v.end());
    for(int i = 0;i <= n;i++)//离散化,使其下标从1开始
        s[i] = lower_bound(v.begin(),v.end(),s[i]) - v.begin() + 1;
    
    for(int i = 0;i <= n;i++)   tr[i] = -inf;//若用memset会初始化过多空间，必TLE(最终运行结果至少相差10倍)

    vector<int> f(n + 1);
    for(int i = 1;i <= n;i++)
    {
        add(s[i - 1],f[i - 1] - (i - 1));
        f[i] = max(f[i - 1] + (a[i] < 0 ? -1 : 0),i + sum(s[i] - 1));//sum[i] - 1是为了统计前面的最大值，不算当前自己
    }
    cout << f[n] << endl;
    return ;
}

int main()
{
    IOS;
    int T;
    cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}

C Half Queen Cover

You are given a board with n rows and n columns, numbered from 1 to n. The intersection of the a-th row and b-th column is denoted by (a,b).

A half-queen attacks cells in the same row, same column, and on one diagonal. More formally, a half-queen on (a,b) attacks the cell (c,d) if a=c or b=d or a−b=c−d.

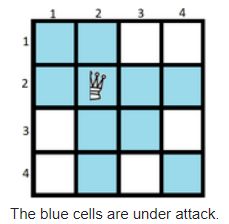
What is the minimum number of half-queens that can be placed on that board so as to ensure that each square is attacked by at least one half-queen?
Construct an optimal solution.
Input
The first line contains a single integer n (1 ≤ n ≤ 10⁵) — the size of the board.

Output
In the first line print a single integer k — the minimum number of half-queens.

In each of the next k lines print two integers a_i, b_i (1 ≤ a_i,b_i ≤ n) — the position of the i-th half-queen.

If there are multiple solutions, print any.
Examples
input
1
output
1
1 1
input
2
output
1
1 1
input
3
output
2
1 1
1 2
Note
Example 1: one half-queen is enough. Note: a half-queen on (1,1) attacks (1,1).

Example 2: one half-queen is enough too. (1,2) or (2,1) would be wrong solutions, because a half-queen on (1,2) does not attack the cell (2,1) and vice versa. (2,2) is also a valid solution.

Example 3: it is impossible to cover the board with one half queen. There are multiple solutions for 2 half-queens; you can print any of them.
题解：
设最少用了k个皇后，则k个皇后占据了k行和k列，还剩下n - k行和n - k列，这些需要利用这k个皇后的对角线来填充，其一共有2 * (n - k) - 1个对角线，即需要满足 k >= 2 * (n - k) - 1，故 k >= (2 * n - 1) / 3，故答案为(2 * n - 1) / 3向上取整。剩下就是构造了，需要自己画图去尝试理解下这种摆法。

#include 

using namespace std;

#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)

int main()
{
	IOS;
	int n;
	cin >> n;

	int k = ceil((2 * n - 1) / 3.0);//细节除以3.0
	cout << k << endl;

	for(int i = 1,j = 1;i <= k;i++)
	{
		cout << i << " " << j << endl;
		j += 2;
		if(j > k)	j = 2;
	}
	return 0;
}
/*
ceil:向上取整函数
floor:向下取整函数
注意：函数里面的数需要为实数，不然上面两个函数用跟没用一样了。
*/

D Edge Elimination

You are given a tree (connected, undirected, acyclic graph) with n vertices. Two edges are adjacent if they share exactly one endpoint. In one move you can remove an arbitrary edge, if that edge is adjacent to an even number of remaining edges.

Remove all of the edges, or determine that it is impossible. If there are multiple solutions, print any.

Input
The input consists of multiple test cases. The first line contains a single integer t (1 ≤ t ≤ 10⁵) — the number of test cases. The description of the test cases follows.

The first line of each test case contains a single integer n (2 ≤ n ≤ 2⋅10⁵) — the number of vertices in the tree.

Then n−1 lines follow. The i-th of them contains two integers ui, vi (1 ≤ u_i,v_i ≤ n) the endpoints of the i-th edge. It is guaranteed that the given graph is a tree.

It is guaranteed that the sum of n over all test cases does not exceed 2⋅10⁵.

Output
For each test case print “NO” if it is impossible to remove all the edges.

Otherwise print “YES”, and in the next n−1 lines print a possible order of the removed edges. For each edge, print its endpoints in any order.
Example
input
5
2
1 2
3
1 2
2 3
4
1 2
2 3
3 4
5
1 2
2 3
3 4
3 5
7
1 2
1 3
2 4
2 5
3 6
3 7
output
YES
2 1
NO
YES
2 3
3 4
2 1
YES
3 5
2 3
2 1
4 3
NO
Note
Test case 1: it is possible to remove the edge, because it is not adjacent to any other edge.

Test case 2: both edges are adjacent to exactly one edge, so it is impossible to remove any of them. So the answer is “NO”.

Test case 3: the edge 2−3 is adjacent to two other edges. So it is possible to remove it. After that removal it is possible to remove the remaining edges too.

E Centroid Probabilities

Consider every tree (connected undirected acyclic graph) with n vertices (n is odd, vertices numbered from 1 to n), and for each 2 ≤ i ≤ n the i-th vertex is adjacent to exactly one vertex with a smaller index.

For each i (1 ≤ i ≤ n) calculate the number of trees for which the i-th vertex will be the centroid. The answer can be huge, output it modulo 998244353.

A vertex is called a centroid if its removal splits the tree into subtrees with at most (n−1) / 2 vertices each.
Input
The first line contains an odd integer n (3 ≤ n < 2⋅10⁵, n is odd) — the number of the vertices in the tree.

Output
Print n integers in a single line, the i-th integer is the answer for the i-th vertex (modulo 998244353).
Examples
input
3
output
1 1 0
input
5
output
10 10 4 0 0
input
7
output
276 276 132 36 0 0 0
Note
Example 1: there are two possible trees: with edges (1−2), and (1−3) — here the centroid is 1; and with edges (1−2), and (2−3) — here the centroid is 2. So the answer is 1,1,0.

Example 2: there are 24 possible trees, for example with edges (1−2), (2−3), (3−4), and (4−5). Here the centroid is 3.