算法训练营第十五天| 层序遍历、LeetCode226.翻转二叉树 、LeetCode101.对称二叉树 2
理解之后,可以刷一下同一类型的10道题:
102. 二叉树的层序遍历
107.二叉树的层次遍历II
199.二叉树的右视图
637.二叉树的层平均值
429.N叉树的层序遍历
515.在每个树行中找最大值
116.填充每个节点的下一个右侧节点指针
117.填充每个节点的下一个右侧节点指针II
104.二叉树的最大深度
111.二叉树的最小深度
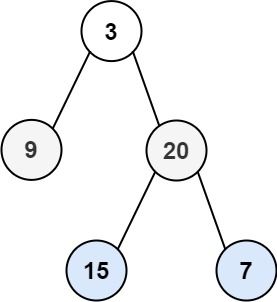
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
queue=[]
res=[]
if not root:
return res
queue.append(root)
while queue:
q_size=len(queue)
q_list=[]
while q_size>0:
node=queue.pop(0)
q_list.append(node.val)
q_size-=1
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
res.append(q_list)
return res
226. 翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
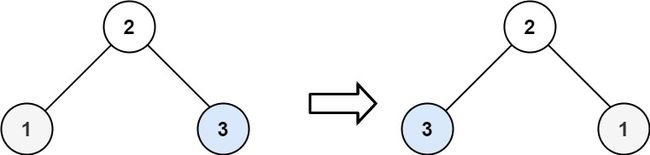
输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]
输入:root = [2,1,3] 输出:[2,3,1]
解法一:使用递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
# 递归法-前序遍历-中左右
# 先处理中间节点,把中间节点的左右子节点进行交换
# 再处理左子树
# 最后处理右子树
def invert(cur):
if cur == None:
return # 当节点为空时,结束本层递归
# 处理当前节点的左右子节点,将左右子节点进行交换
cur.left, cur.right = cur.right, cur.left
invert(cur.left) # 再进行处理节点的左子树
invert(cur.right) # 处理节点的右子树
invert(root)
return root解法二:使用迭代法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
# 迭代法
stack = []
cur = root
if not root:
return root
stack.append(root) # 将根节点入栈
while stack:
node = stack.pop() # 将栈中的最后一个节点弹出
# 将节点的左右子节点进行交换
node.left, node.right = node.right, node.left
# 如果节点的左子节点不为空,将左节点入栈
if node.left:
stack.append(node.left)
# 如果节点的右子节点不为空,将右节点入栈
if node.right:
stack.append(node.right)
return root解法三:使用层序遍历
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
# 层序遍历
queue = []
if not root:
return root
queue.append(root) # 将跟节点入栈
while queue:
q_len = len(queue) # 统计每层的节点数
while q_len > 0: # 每层剩余的节点数不为0时
node = queue.pop(0) # 弹出第一个节点
# 将节点的左右子节点进行交换
node.left, node.right = node.right, node.left
q_len -= 1 # 弹出节点后,每层剩余的节点数减1
# 弹出节点的左节点不为空,将左节点加入栈
if node.left:
queue.append(node.left)
# 弹出节点的右节点不为空,将右节点加入栈
if node.right:
queue.append(node.right)
return root
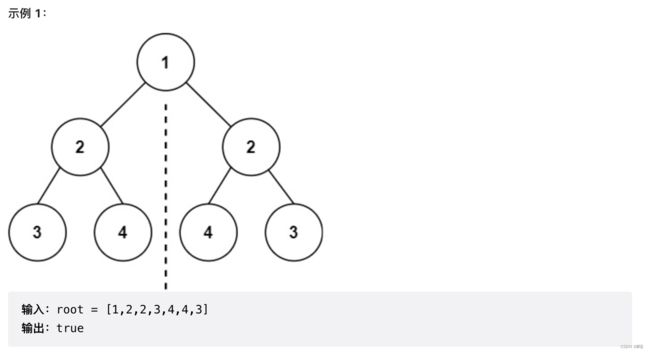
101. 对称二叉树
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
def symmetric(cur1, cur2):
if cur1 == None and cur2 == None:
return True # 当cur1,cur2都为空
if cur1 == None and cur2 != None:
return False # 当cur1为空,cur2不为空,说明不对称
if cur1 != None and cur2 == None:
return False # 当cur1不为空,cur2为空,说明不对称
if cur1.val != cur2.val:
return False # 当cur1,cur2对应的值不相等,说明不对称
# 当cur1不为空,cur2不为空,cur1,cur2的值相等,则继续比较子节点
# 需要比较cur1的左节点,和cur2的右节点,即对比外侧的节点是否对称
outside = symmetric(cur1.left, cur2.right)
# 比较cur1的右节点,和cur2的左节点,即对比内侧的节点是否对称
inside = symmetric(cur1.right, cur2.left)
# 获取内侧和外侧对比的结果,进行返回
result = outside and inside
return result
res=symmetric(root.left,root.right)
return res