Leetcode动态规划题

动态规划

基本思想：问题的最优解如果可以由子问题的最优解推导得到，则可以先求解子问题的最优解，再构造原问题的最优解；若子问题有较多的重复出现，则可以自底向上从最终子问题向原问题逐步求解。
使用条件：可分为多个相关子问题，子问题的解被重复使用。
基本步骤：

• 首先创建一个存放子问题的解的空间，并做初始化。
• 将原问题尝试拆成多个子问题，并使得子问题的解可以求出原问题的解，这个通过子问题解求出原问题解的方程就叫做状态转移方程。
• 根据状态转移方程自底向上得到原问题解。
• （附加）有时候存放子问题的解的空间可以优化得更小。

根据动态规划的题目，我分成了以下的做法：

• 如果题目是要求你求：数组中相邻的得分问题，且标记过的数不能再标记，那么这就是斐波那契数列型的动态规划，dp[i]要么选择不用当前的数组元素计分并沿用之前的最优解（类似于dp[i] = dp[i-1]），要么选择使用当前的元素计分（类似于dp[i] = dp[i-2] + num[i]），再去选两种方法的最优解即可。
• 如果题目给了你一张地图，并且求人走地图的点数最优解，那么这就是矩阵路径型的动态规划，根据路径设置dp即可，这种也是最简单的动态规划。
• 如果需要求数组子区间符合某种规律的个数，例如等差数列，那么这种动态规划可以根据规律的特性做延申。例如，如果当前的数和前面的数形成了等差数列，而前面的数也和更前面的数形成了等差数列，那么等差数列的性质就会传递。
• 如果需要求数组的最大（最长）公共子序列，那可以用内外两轮循环对数组遍历，外轮正向，内轮从外轮的指针开始往反向循环判断；或者也可以参考斐波那契数列的解法。
• 如果给了一个阈值，让你求积累到这个阈值的最大价值/最小元素数量，那么这就是0-1背包问题。0-1背包问题的思想就是根据前 i 个物品，在容量最大为 j 的价值 dp[i][j]；根据问题变种，可能会出现多种维度的背包问题（重量和体积都算进去，放入背包时需要两个条件都符合）；还有完全0-1背包问题（物品数量无限，求出最大价值），此时 i 表示的不是前 i 个物品，而是前 i 种物品。
  • 0-1背包的状态方程：dp[i][j] = dp[i-1][j-w] + v。
  • 完全0-1背包的状态方程：dp[i][j] = dp[i][j-w] + v。

---

斐波那契数列

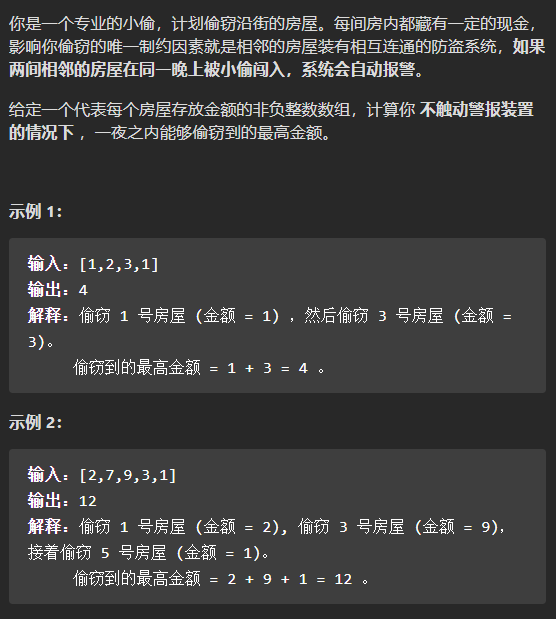
1. 打家劫舍

链接：打家劫舍

这是非常经典的斐波那契数列类型的动态规划题。使用一个数组dp来表示前n个房屋中能偷窃的最高金额。因为不能连续偷两家，也就是说在选择第 i-1 家和第 i-2 家与第 i 家相比，选更大的那个。

class Solution {
   
    public int rob(int[] nums) {
   
        int n = nums.length;
        if(n<=1) return nums[0];
        int[] dp = new int[n];

        dp[0] = nums[0];
        dp[1] = Math.max(dp[0], nums[1]);

        for(int i = 2; i<n; i++){
   
            dp[i] = Math.max(dp[i-1], dp[i-2]+nums[i]);
        }
        return dp[n-1];
    }
}

2. 相邻字符串（网易互联网）

给出一个字母字符串，如果相邻两个字母相同或者在字母表中相邻，则标记这两个字母，并把这两个字母的分数加到你获得的分数中，‘a’等于1，‘b’等于2，以此类推，要求被标记过的不能再使用。求最大的分数。

这道题是一个很典型的动态规划题，用一个数组dp来记录最大的分数，dp[i]表示区间[0:i]内的最大分数。由于题目要求标记过的字母不能再使用，那么当i-2, i-1, i三个下标内的字母都满足标记的条件的话，就只能选择i-2, i-1或者i-1, i这两种组合中会得分最高的一种。

package Test;
import java.util.*;

public class Main {
   
    public static void main(String[] args) {
   
        Scanner sc = new Scanner(System.in);
        String s = sc.next();
        int[] dp = new int[s.length()];
        dp[0] = 0;
        dp[1] = getSum(s.charAt(0), s.charAt(1));

        for (int i = 2; i < s.length(); i++) {
   
            dp[i] = Math.max(dp[i-1], dp[i-2]+getSum(s.charAt(i), s.charAt(i-1)));
        }
        System.out.println(dp[s.length()-1]);


    }

    public static int getSum(char a, char b) {
   
        int x = a - 'a' + 1;
        int y = b - 'a' + 1;
        if (Math.abs(x - y) <= 1) {
   
            return x + y;
        }
        return 0;
    }

}

参考：https://leetcode-cn.com/problems/longest-common-subsequence/solution/zui-chang-gong-gong-zi-xu-lie-by-leetcod-y7u0/

---

矩阵路径

1. 不同路径

链接：不同路径

动态规划最关键的就是找到状态转移方程。在本题目中，我们的目的是找到机器人到星的路径数量。我们用子问题求解原问题的思路上去想。

由于机器人只能向右或者向下移动，那么我们很容易就能发现，机器人到达终点左边和上面的格子所需要的路径数，就是子问题的解。通过将这两个路径数相加，我们就能得到这个问题的解。这里我们就通过了星星前一步的子问题求解了原问题。

建立状态方程：f(i, j) = f(i-1, j) + f(i, j-1)

解题如下，此时时间复杂度O(mn)，空间复杂度O(mn)

class Solution {
   
    public int uniquePaths(int m, int n) {
   
        int[][] nums = new int[m][n];
        for(int i = 0; i<m; i++){
   
            nums[i][0] = 1;
        }
        for(int i = 0; i<n; i++){
   
            nums[0][i] = 1;
        }
        for(int i = 1; i<m; i++){
   
            for(int j = 1; j<n; j++){
   
                nums[i][j] = nums[i-1][j]+nums[i][j-1];
            }
        }
        return nums[m-1][n-1];
    }
}

优化：由于只需要前一条网格的路径数，所以存放子问题解的空间可以优化。下面代码空间复杂度O(n)。

class Solution {
   
    public int uniquePaths(int m, int n) {
   
        int[] pre = new int[n];
        int[] cur = new int[n];
        Arrays.fill(pre, 1);
        Arrays.fill(cur,1);
        for (int i = 1; i < m;i++){
   
            for (int j = 1; j < n; j++){
   
                cur[j] = cur[j-1] + pre[j];
            }
            pre = cur.clone();
        }
        return pre[n-1]; 
    }
}

进一步优化：

class Solution {
   
    public int uniquePaths(int m, int n) {
   
        int[] cur = new int[n];
        Arrays.fill(cur,1);
        for (int i = 1; i < m;i++){
   
            for (int j =