CodeTON Round 2 (Div. 1 + Div. 2, Rated, Prizes! (A - D 题解)

CodeTON Round 2 (Div. 1 + Div. 2, Rated, Prizes!)

A. Two 0-1 Sequences

原题：

题目大意：

两个长度为n和m的二进制序列a和b（题目保证n >= m）

两个操作：

op1:

改变a(2) 为min(a(1), a(2)),并且移除a（1）

op2:

改变a(2) 为max(a(1), a(2)),并且移除a（1）

每次操作后，原先的a(i)变成a(i + 1), 长度减少1，即前移。

问：a二进制序列能否通过这两个操作变成b二进制序列。

思路分析：

保证a序列的后m - 1位和b序列是一致的，并且，a序列a[1] 到 a[n - m + 1]中存在b[1]即可通过两个操作将a变化成b.

**原因：**这两个操作只能改变最终得到序列的第一个位置的数。

代码：

#include 
#include 
using namespace std;
const int N = 55;
int t, n, m;
int a[N], b[N];
void solve(){
    scanf("%d %d", &n, &m);
    for(int i = 1; i <= n; i ++)scanf("%1d", &a[i]);
    for(int j = 1; j <= m; j ++)scanf("%1d", &b[j]);

    for(int i = n, j = m; j >= 2; i --, j --){
        if(a[i] != b[j]){
            printf("NO\n");
            return;
        }
    }

    for(int i = 1; i <= n - m + 1; i ++){
        if(a[i] == b[1]){
            printf("YES\n");
            return;
        }
    }
    printf("NO\n");
    return;
}

int main(){
    cin >> t;
    while(t --){
        solve();
    }
    return 0;
}

B. Luke is a Foodie

原题：

题目大意：

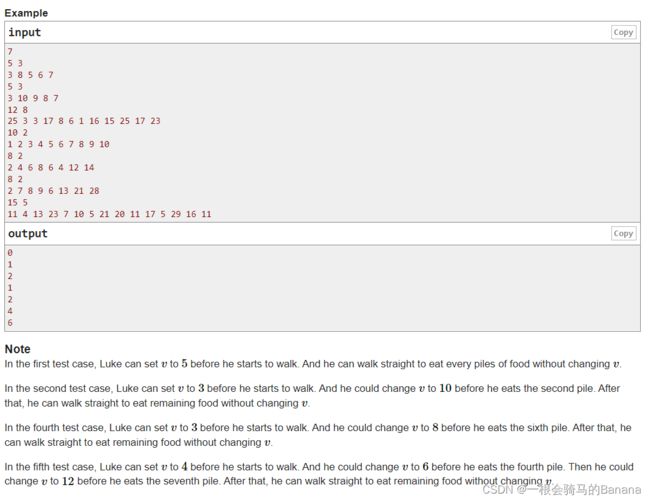
对于a数组中的每一个元素，满足 |v−ai|≤x， （x是固定的值，由题目给出， v是可以变化调动的值）

问最少需要调动几次v，才能使得a数组中所有元素满足|v−ai|≤x

思路分析：

对于每一个元素，v取值要满足公式，都有一个上下界[ai - x, ai + x]。

对于之后的每一个元素上下界，我们只需要调动v的上下界的值在该元素上下界范围内即可，如果某个元素的上下界不在v的上下界 范围内， 那么就说明必须要变化一次v的值，为当前数的上下界即可。

代码：

#include 
#include 
using namespace std;
const int N = 2e5 + 5;
int t, n, x;
int a[N];
int main(){
    cin >> t;
    while(t --){
        cin >> n >> x;
        for(int i = 1; i <= n; i ++)cin >> a[i];
        int l = a[1] - x, r = a[1] + x;
        int cnt = 0;
        for(int i = 2; i <= n; i ++){
            if(a[i] - x > r || a[i] + x < l){
                cnt ++;
                l = a[i] - x;
                r = a[i] + x;
                continue;
            }
            l = max(l, a[i] - x);
            r = min(r, a[i] + x);
        }
        cout << cnt << '\n';
    }
    return 0;
}

C. Virus

原题：

题目大意：

一个圆圈内有n个房子（编号为：1、 2、 3 …… n 、 1），最初，其中的m个房子被感染了，每天被感染的房子会感染其相邻的房子（该房子未被感染或未被保护）.Cirno每天可以选择一个房子保护，使他永久免疫。问Cirno在最合理的操作下，使房子感染数量最少， 输出最终房屋感染的数量。

思路分析：

先预处理出感染房子之间未被感染房子的数量，为了使得最终房屋感染数量最少，我们按照感染房子之间未被感染房子的数量从大到小进行保护即可。

代码：

#include 
#include 
#include 
using namespace std;
const int N = 1e5 + 5;
int t, n, m;
int a[N], res[N];
bool cmp(int a, int b){
    return a > b;
}
int main()
{
    cin >> t;
    while(t --){
        cin >> n >> m;
        for(int i = 1; i <= m; i ++)cin >> a[i];
        sort(a + 1, a + 1 + m);
        for(int i = 1; i < m; i ++){
            res[i] = a[i + 1] - a[i] - 1;
        }
        res[m] = n - (a[m] - a[1]) - 1;
        sort(res + 1, res + m + 1, cmp);

        int k = 0, cnt = 0;
        for(int i = 1; i <= m; i ++){
            //cout << cnt << '\n';
            if(res[i] - 2 * k > 0){
                if(res[i] - 2 * k == 1)cnt ++;
                else cnt += res[i] - 2 * k - 1;
            }
            k += 2;
        }

        cout << n - cnt << '\n';
    }
    return 0;
}

D. Magical Array

原题：

题目大意：

定义一个特殊行，执行操作2，其它行执行操作1（执行次数都至少有一次）

给出这些行，让你输出那个是特殊行，以及特殊行操作2的次数。

思路分析：

op1:
i * a(i) + j * a(j)
= i * (a(i) - 1) + j * (a(j) - 1) + (i - 1) * (a(i - 1) + 1) + (j + 1) * (a(j + 1) + 1)
= i * a(i) - i + j * a(j) - j + (i - 1) * a(i - 1) + (i - 1) + (j + 1) * a (j + 1) + (j + 1)
= -i - j + (i - 1) + (j + 1)
= 0
op1 操作不改变原来该数组的sum

op2:
i * a(i) + j * a(j)
= i * (a(i) - 1) + j * (a(j) - 1) + (i - 1) * (a(i - 1) + 1) + (j + 2) * (a(j + 2) + 1)
= +1
op2 操作使得该数组原来的sum + 1

代码：

#include 
#include 
#include 
#include 
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
int t, n, m;
ll sum[N];
vector<ll>ve[N];
int main()
{
    cin >> t;
    while(t --){
        cin >> n >> m;
        ll maxm = -1e18, minm = 1e18;
        for(int i = 1; i <= n; i ++){
            sum[i] = 0;ve[i].clear();
            for(int j = 1; j <= m; j ++){
                int x;
                cin >> x;
                ve[i].push_back(x);
                sum[i] += ve[i][j - 1] * j;
            }
            maxm = max(maxm, sum[i]);
            minm = min(minm, sum[i]);
        }
        for(int i = 1; i <= n; i ++){
            if(sum[i] == maxm){
                cout << i << ' ' << maxm - minm << '\n';
            }
        }
    }
    return 0;
}