第五届传智杯初赛B组题解

A-莲子的软件工程学

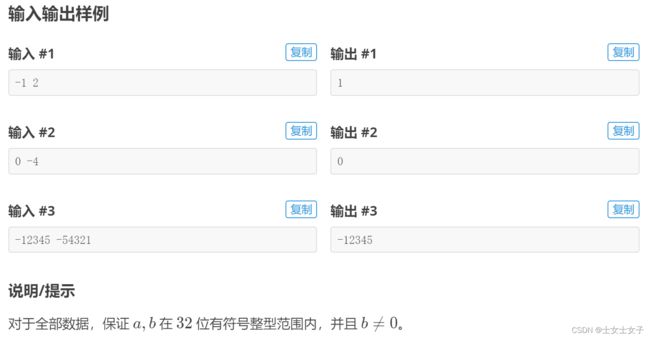
 【题解】这是一个简单的编程题，如果b大于0，a为正整数，b小于0，a为负整数。但是要注意，java写的时候要用long类型！！！

代码：

import java.util.Scanner;

public class A {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        long a = sc.nextLong();
        long b = sc.nextLong();
        if (b > 0) {
            System.out.println(Math.abs(a));
        } else {
            System.out.println(-Math.abs(a));
        }
    }
}

B-莲子的机械动力学

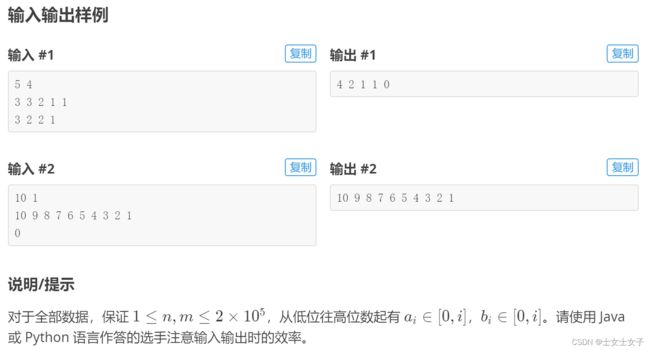
 【题解】这个题是进制相加问题，首先输入两个数的长度，由于每个数都是由高位到低位描述数码，我们可以先将长度较短的那个数字进行前补0的操作，这样最后相加的时候两个数的长度相同。然后将两个数的每一位按顺序放入两个list中，进行从低位开始的a+b的操作。由于最低位进制从2开始依次递增，我们可以在相加的时候用两个变量分别表示进制位和是否有进位。再由一个list记录答案即可。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.ArrayList;
import java.util.List;

public class Main{
	static Listlista = new ArrayList<>();
	static Listlistb = new ArrayList<>();
	public static void main(String[] args) throws IOException {
		StreamTokenizer re = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
		re.nextToken();
		int n = (int)re.nval;
		re.nextToken();
		int m = (int)re.nval;
		if(n - m > 0) {//判断n和m哪个数更大，让小的数进行前置0操作
			int x = n - m;
			for(int i = 0; i < x; i++)	listb.add(0);
		}else {
			int x = m - n;
			for(int i = 0; i < x; i++)	lista.add(0);
		}
		for(int i = 0 ; i < n; i++) {//将n和m放入list中
			re.nextToken();
			lista.add((int)re.nval);
		}
		for(int j = 0; j < m; j++) {
			re.nextToken();
			listb.add((int)re.nval);
		}
		int k = Math.max(n, m) - 1;//操作的次数
		Listans = new ArrayList<>();//记录答案
		int pos = 2,cnt = 0;//pos标记第几进制，从2开始递增；cnt表示是否需要进位
		for(int i = k; i >= 0; i--) {//从低位开始相加
			int x = lista.get(i) + listb.get(i) + cnt;
			if(x >= pos) {
				cnt = 1;
				x -= pos;
			}else cnt = 0;
			ans.add(0,x);
			pos++;
		}
		if(cnt == 1)	ans.add(0,1);//如果最后一位还有进位要加进去
		PrintWriter wr = new PrintWriter(new OutputStreamWriter(System.out));
		for(Integer an : ans) {//从高位到低位进行输出
			wr.print(an+" ");
		}
		wr.flush();
		wr.close();
	}
}

D-莲子的物理热力学

 【题解】这是一个贪心题，我写的时候觉得太不可思议了，这种每走一步都会涉及到下一步甚至下面几步的贪心，情况太多了一点也不好考虑，也太难啦吧，为什么会放在D题呀，呜呜呜。。。写的时候真没有想到方法，比完之后看了巨巨的题解，然后在这里总结分享一下啦。

        假设经过m次操作最后得到数字的值域为[l,r],那么l左边的数严格小于l，r右边的数也严格大于r。令a中小于l的个数为u,大于r的个数为v,那么至少的操作次数为u+v+min(u,v);

证明：

        要想让左边数的最小值为l,那么左边至少操作u次，同理如果想让右边的值为r,那么右边至少操作v次，但是要使m的操作次数最少，我们还要操作min(u,v)次（如果左边的数先变大操作到右边，那么右边的数值要想变小，需要先将左边变大的数值先变小，要想操作次数最少，所以取最小值）。

做法：

1. 先将数组a进行从小到大排序
2. 先将l = ai进行枚举，计算出r = aj,需要满足条件 (i - 1) + (n - j) + min(i - 1,n - j) <= m
3. 当i递增时，j也会单调递增，因此可以找到满足条件的最小的j
4. 由于最多可以操作m次，而且1 <= n <= 10^5, 1 <= m <= 10^9,所以i <= min(n,m+1),当m == 0时，进行一次操作即可。

代码：

import java.util.Arrays;
import java.util.Scanner;

public class Main{
	static int N = 100010;
	static int a[] = new int[N];
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int m = sc.nextInt();
		for(int i = 1; i <= n; i++) {
			a[i] = sc.nextInt();
		}
        //法一：先判断m是否大于n
        //if(m > n) {
        //   System.out.println(0);
        // return;
        //}
		Arrays.sort(a,1,n+1);//排序
		int j = 1,ans = Integer.MAX_VALUE;
		for(int i = 1; i <= Math.min(n, m+1); i++) {//枚举l
            //法二：取i,j的最大值
			j = Math.max(i, j);//计算满足条件时j的最小值
            //当m > n时，j一直为1，会存在j < i的情况，j = Math.max(i, j);存在的意义是防止j < i
			while((i-1) + (n - j) + Math.min(i-1, n-j) > m)	j++;
			ans = Math.min(ans, a[j] - a[i]);//记录最小值
		}
		System.out.println(ans);
		sc.close();
	}
}

E-梅莉的市场经济学

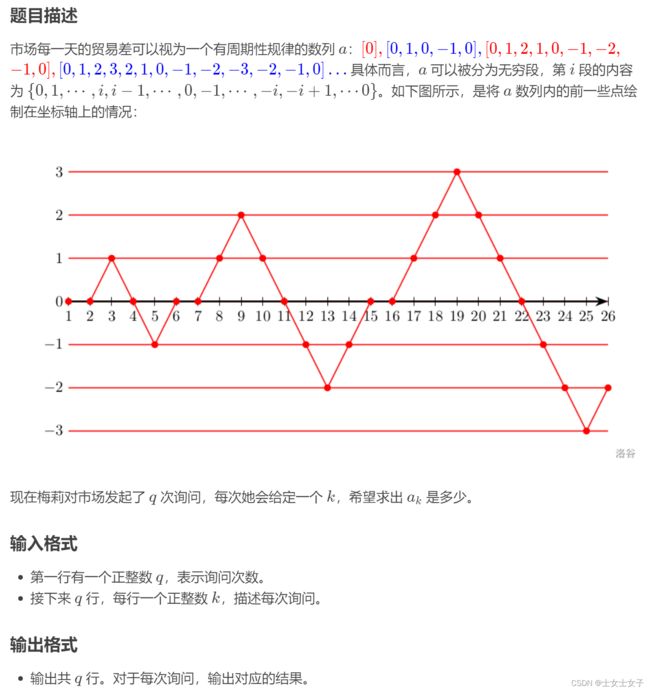
【题解】 本题是输出一个数，让我们找个这个数的坐标的值为多少。

1. 首先我们应该明确这个数应该在哪一个段，
2. 其次是找到在这一段的哪一个位置，
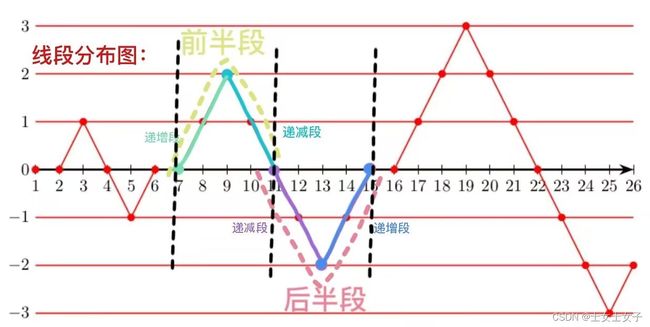
3. 每一段内也是有规律的，前半段是大于等于0，而后半段是小于等于0，前半段又可分为两段，前面是单调递增的，后面是单调递减的；后半段是先递减后递增，第n段的最大值最小值也可以求，由此可以解题。
4. 下图为具体某段，可帮助理解：

通过题目描述我们可以得知，数列a是一个等差数列：

第n段	段落内容	第n段大小	段落最大值
1	[0]	1	0
2	[0,1,0,-1,0]	5	1
3	[0,1,2,1,0,-1,-2,-1,0]	9	2
...	...	...	...

由上方表格得知，每后一个段落比前一个的个数大4，第一个段落个数为1，由此得知这个数列是首项为1，公差为4的等差数列。得到这个重要条件后，这个数是在哪一段以及在那一段的哪个位置也可求出。

• 求k在哪一段：

        前n项和的求和公式：Sn = n * a1 + n * (n - 1) / 2 * d;

        已知a1 = 1,d = 4, Sn = 2 * n^2  - n;

        如果Sn >= k (2 * n^2 - n >= k ),说明k包含在第n段内，

        这里我们需要计算一下n的最大和最小的范围，然后用二分来确定n的值：

         由上可得1 <= n <= 3 * 10^9。

        k =k - ( 2 * (n - 1)^2 - (n - 1)); 用k将前n段和减去所得的值即为第n段的第k个

• 求第n段的k个位置的值：

        第n段的个数：an = a1 + (n - 1) * d;(通项公式）

        已知a1 = 1,d = 4, an =4 * (n - 1) + 1;

        第n段的最大值为：max = n-1,最小值为：min = -（n-1)

        分情况讨论：

        1.an / 2 >=k，说明k在an的前半段,ans>= 0;

              然后需要再判断k在an的递增段还是递减段：（先递增后递减）

               (1) 如果n-1 >= k,说明k 在an的递增段，ans = k - 1;

                (段落的值从0开始，第k个的值为k-1)

               (2)如果n-1 < k,说明k在an的递减段(递减段中包含了最大值)，k首先需要减去递增段的长度：k - (n - 1),然后让递减段的长度减去k的长度：

                 ans = (n-1) - （k - （n - 1)) + 1 = n  * 2 - k - 1;

      2.an / 2 < k，说明k在an的后半段，k需要先减去前半段的长度（k = k - an / 2）,  再让第n段的长度减半加1，得到后半段的长度（an = an /  2 + 1）,ans <= 0；

        

                 然后需要再判断k在an的递减段还是递增段：（先递减后递增）

                （1）如果an / 2 >= k，说明k在an的递减段，ans = -(k - 1);

                   (段落的值从0开始，第k个的值为k-1)

                （2）如果an / 2 < k，说明k在an的递增段，ans = -(n * 2 - k - 1);

代码：

import java.util.Scanner;

public class Main{
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int q = sc.nextInt();
		while(q-- > 0) {
			long k = sc.nextLong();
			long l = 1,r =(long) 3e9;
			while(l < r) {
				long mid = (l + r) >> 1;
				if(2 * mid * mid - mid >= k)	r = mid;
				else l = mid + 1;
			}
//			System.out.println("l:"+l);
			long n = l;
			int ans = 0;
			long an = 4 * (n - 1) + 1;//第n段的长度
			k = k - ( 2 * (n-1) * (n-1) - (n-1));
			if(an / 2 >= k) {//前半段
				if(k <= (n - 1)) {//递增段
					ans = (int) (k - 1);
				}else {//递减段
					ans = (int)(2 * n - k - 1);//((n-1) - (k - (n - 1)) + 1)
					//k需要先减去递增段的长度,然后让递减段的长度减去k,+1是因为递减段是从最大值开始的
				}
			}else {//后半段
				k -= an / 2;//k先减去前半段的长度
				an = an / 2 + 1;//每一段都是奇数，我们约定让后半段比前半段多1
				if(k <= an / 2) {//递减段
					ans = -(int)(k - 1);
				}else {//递增段
					ans = -(int)(2 * n - k - 1);//((n-1) - (k - (n - 1)) + 1)
				}
			}
			System.out.println(ans);
		}
	}
}

有待更新。。。